这一年差不多刷了300多道leetcode的题目,虽然看起来挺多的但是一下子让我再去重新写出来,一下子还是写不出来。所以计划着重新把中等题再回顾下,温故而知新还是挺有意思的过程。话不多说让我们来看看这道题
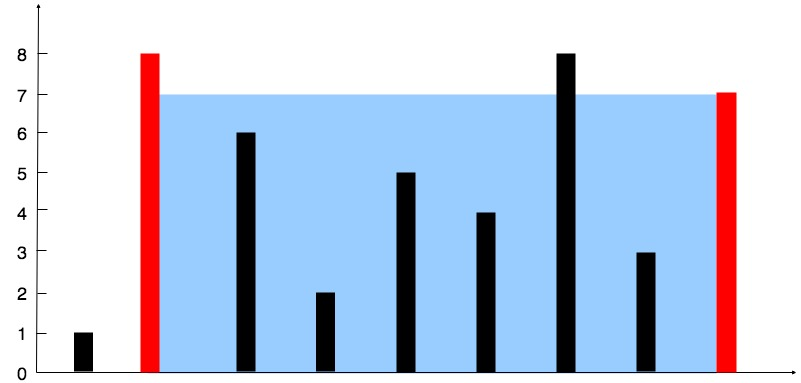
给定 n 个非负整数 a1,a2,...,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明:你不能倾斜容器,且 n 的值至少为 2。
图中垂直线代表输入数组[1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例:
输入: [1,8,6,2,5,4,8,3,7] 输出: 49
这道题用一个公式可以表示出来
Sum = Math.min(H[i], H[j]) * (j-i)
看到 i j 那么我们就可以联想到这道题应该就是用双指针去遍历 那么结束条件就是 j>=i
while(i<j){
// TODO
}
这里就涉及到了i和j在什么时机去移动, 应该如何移动。这里我们先给出答案。
if (H[i] < H[j]){
i++
} else {
j--
}
一句话:朝着指针向高数值的一边去移动。
难道这样就能保证两个指针在移动的时候,
不会落掉一些情况吗,毕竟我们从 n*n / 2的比较次数 降低到n的比较次数。
我们从两个指针的起始位置开始分析 i=0, j = 7
这时候我们有两个选择 要么 i++ 要么 j--
-
选择i++的时候,H[1] 虽然变大了 但是 j - i 的值也相应变小了,所以这个选择不是绝对的能获取到最大值。
-
那么我们再看j-- 在这个选择中 我们回顾下之前的公式发现
- H[6]要么比H[0]大 Math.min(H[0], H[6])还是H[0], 这个情况下Sum[0,6]的值是要小于S[0,7]因为j-i的值变小了 第二种情况
- H[6]比H[0]小 那么Math.min(H[0], H[6])是H[6]这种情况下 Sum[0,6] 还是小于Sum[0,7]
由此我们可以肯定Sum[0,6]一定要比Sum[0,7]小,题目要求的是最大值,那么这种情况就舍弃了。这样推断下只能选择Sum[1,7]
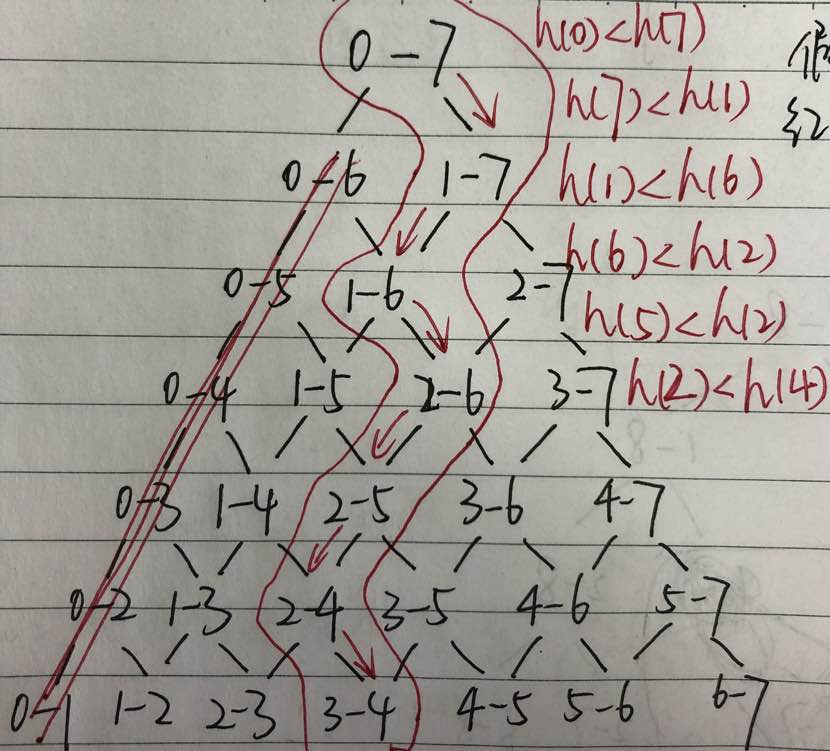
由上图可以知道 我们把整个过程可以看做是一个选择的过程每到一个节点,就去选择可能存在最大值的分支
var maxArea = function (height) {
let max = 0;
for (let i = 0, j = height.length - 1; i < j;) {
max = Math.max(max, (j - i) * (height[i] < height[j] ? height[i++] : height[j--]))
}
return max;
};