本文是刷leetcode第207题的感想,《算法》4th english version这本书已经很久没看了,尝试自己写出有向图的leetcode题,心想以前在公司项目里撸过DAG(有向无环图),现在做题肯定不在话下,而且正好检测一下学习成果,也能看看自己的理解是否深刻。
结果做倒是做出来了,就是时间惨不忍睹(250ms,仅超越约6%),很尴尬,再看了看书,发现以前对书上算法的理解有问题,特此记录。
我的做题思路
class Solution {
public boolean canFinish(int numCourses, int[][] prerequisites) {
//完成所有课程,说明没有环(有环就互为前置了)
//需要都可达吗? 不需要。。并没有这个需求
Object[] adj = new Object[numCourses];
boolean[] onStack = new boolean[numCourses];
//构造出邻接链表,这不重要
int i = prerequisites.length;
for(int j = 0;j<i;j++){
Integer left = prerequisites[j][1];
Integer right = prerequisites[j][0];
if(adj[right] == null){
Set<Integer> set = new HashSet<>();
set.add(left);
adj[right] = set;
}else{
Set<Integer> set = (Set<Integer>)adj[right];
set.add(left);
adj[right] = set;
}
}
//对每个节点进行一次dfs,如果发现一次循环之后有环就退出
for(int k = 0;k<numCourses;k++){
boolean b = dfs(k,adj,onStack);
if(b==false){return false;}
}
return true;
}
private boolean dfs(int i, Object[] adj, boolean[] onStack){
//是否在方法调用栈上,也就是,是否在来当前节点的路径上
//这里的栈,其实是方法调用栈的思想,思想是栈,但是为了能随意获取某个元素用了数组
onStack[i] = true;
Set<Integer> set = (Set<Integer>)adj[i];
if(set == null){
onStack[i] = false;
return true;};
for(Integer integer: set){
if(onStack[integer]==true){
return false;}
boolean b = dfs(integer,adj,onStack);
if(!b){return b;}
}
onStack[i] = false;
return true;
}
}
与书上算法的区别
public class DirectedCycle {
private boolean[] marked; // marked[v] = has vertex v been marked?
private int[] edgeTo; // edgeTo[v] = previous vertex on path to v
private boolean[] onStack; // onStack[v] = is vertex on the stack?
private Stack<Integer> cycle; // directed cycle (or null if no such cycle)
public DirectedCycle(Digraph G) {
marked = new boolean[G.V()];
onStack = new boolean[G.V()];
edgeTo = new int[G.V()];
for (int v = 0; v < G.V(); v++)
if (!marked[v] && cycle == null) dfs(G, v);
}
// check that algorithm computes either the topological order or finds a directed cycle
private void dfs(Digraph G, int v) {
onStack[v] = true;
marked[v] = true;
for (int w : G.adj(v)) {
// short circuit if directed cycle found
if (cycle != null) return;
// found new vertex, so recur
else if (!marked[w]) {
edgeTo[w] = v;
dfs(G, w);
}
// trace back directed cycle
else if (onStack[w]) {
cycle = new Stack<Integer>();
for (int x = v; x != w; x = edgeTo[x]) {
cycle.push(x);
}
cycle.push(w);
cycle.push(v);
}
}
onStack[v] = false;
}
}
看了看书,发现书上的变量比我多两个edgeTo、marked,edgeTo是因为需要记录一下到底环由哪几个节点构成,我们这里只需要检测是否有环,因此edgeTo不需要。
那么再来看marked
- 在DirectedCycle方法中,就已经用到了marked,也就是,如果已经到过的节点,那么就不做dfs了。
- 在dfs中
- 对于没有到过的节点,做dfs
- 到过的节点&在方法调用栈上,就说明有环
- 到过的节点&不在方法调用栈上,说明在其他路径上已经处理过该节点,什么都不做
这里有两个问题:
- 在DirectedCycle方法中,对于到过的节点不做dfs
- 在dfs方法中,对于到过&不在方法调用栈上的节点,什么都不做
也可以说是一个问题:
从其他节点出发到过的节点,或者对其他节点dfs已经处理过的节点,是否能确保是安全的。
这里的安全包括两点:
- 如果已经处理过的路径有环,那么正在处理的路径也有环(这种情况实际不可能存在,因为如果已经处理过的路径有环,那么方法就会退出,也不会处理新的路径了)
- 如果已经处理过的路径无环,假如已经处理过的路径的一部分是正在处理的路径的一部分,那么已经处理过的路径所在的部分无环。(如果包含已处理过路径的正在处理路径有环,那么被包含的部分应该也在环中,该命题成立,则需要被证明的逆否命题也成立)
因此可以得出已被处理过的节点是安全的结论,因此可以忽略marked==true的节点。
我在我的代码中加入了marked优化,直接让执行时间从250ms降低到了6ms!!!
一个小重点
其实有一个重点结论:如果dfs到了存在于环中的某个节点,那么一定会进入环!那么他的逆否命题就是,如果dfs处理过的节点没有进入环,那么该节点一定不在环中
因为节点在环中,那么节点的邻接链表中一定存在一个同样处在环中的节点。这么显而易见的特点,一定一定要利用起来。
误区
之前是直接看的书,没有刷题,有些东西没有想透,比如这个marked,我认为书中的代码,是要实现的功能的最小可用版本,但是marked又看不懂,而for循环又是从0开始的,书上的各种图都是0就是起始节点,因此我认为,只有在从起始结点开始dfs时,这个marked也有用。包括我在做项目时,我也定了一个起始节点。
但是在做题的时候发现,他并没有一个起始节点,我对每一个节点做dfs毫无问题,加上marked之后也毫无问题,于是我发现了,并不需要从一个起始节点开始dfs, 即使一开始dfs的是比较靠后的节点,之后循环的是靠前的节点,那也是没有问题的,而且对这种情况可以做优化。
我以为marked是实现某个功能的,没想到marked是为了优化。但是其实我也能感觉到自己的思路有问题,假设0123是有关联关系的,45是有关联关系的,那难道就一定是4之后是5吗?书中完全没有这样的前提条件,是我自己在瞎想罢了。
之所以没想通,还是因为有向图和无向图的区别其实有点大,无向图中的marked好理解,有向图中的marked还是多了些需要注意的地方。
edgeTo
可以注意到,只有marked[w]为false的时候才添加edgeTo[w]=v,也就是说,对每个节点来说,只有第一次到达这个节点的时候才设置edgeTo,那么这是为什么呢?
会不会edgeTo设置错了?也就是说edgeTo对某个在环中的点设置了不在环中的路径?基于此假设,那么
- 节点V应有某个不在环中的节点指向V
- 节点V在环中
那么V应该是这样的样子:
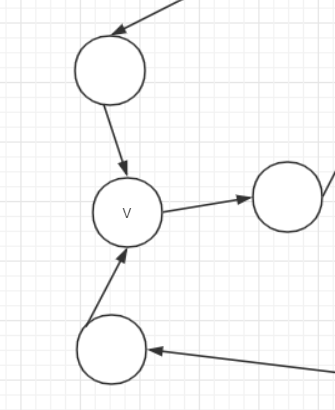
因为V在环中,所以V除了不在环中的节点指向V,其他必然至少有两条路径,一条出,一条入,而这条出的路径又在环中,那么根据代码和画图来看
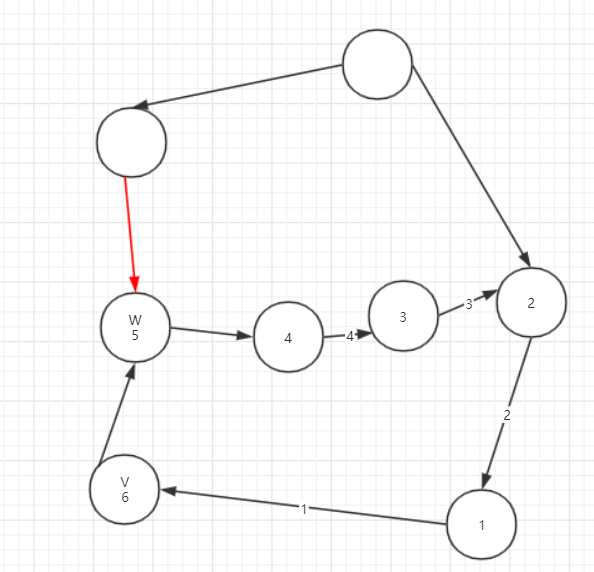
cycle = new Stack<Integer>();
for (int x = v; x != w; x = edgeTo[x]) {
cycle.push(x);
}
cycle.push(w);
cycle.push(v);
总结
今天的策略,即先自己写再看书,今天看起来还是很成功的,不仅如此,以后刷题也要多看高效率的题解,多想着从各个角度解决问题。不过,第一遍目测还是做完拉倒吧哈哈哈哈。