【搞定算法面试】- 二叉树中序遍历下一节点上一期介绍了松散链表的实现，本期我们将探讨二叉树遍历的问题。给出一颗二叉树中

前言

上一期介绍了松散链表的实现，本期我们将探讨二叉树遍历的问题。

题面

给出一颗二叉树中某节点，求该节点以中序遍历的下一节点。

分析

首先我们先回忆下二叉树的中序遍历算法。

二叉树示意图：

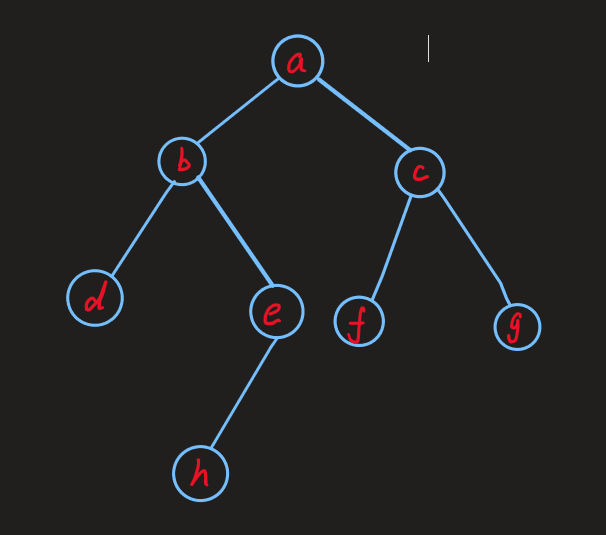
中序遍历： d b h e a f c g

代码实现：

class TreeNode:
    def __init__(self, val, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right
        
def inorder(root):
    stack = []
    cur = root
    while True:
        while cur:
            stack.append(cur)
            cur = cur.left
            
        if not stack:
            break
        cur = stack.pop()
        print(cur.val)
        cur = cur.right

外层循环轮数	栈元素变化	cur节点变化	输出
1	[a,b,d] -> [a,b]	a->b->d->d(pop)->None	d
2	[a,b] -> [a]	None->b(pop)->e	b
3	[a] -> [a,e,h] -> [a,e]	e->h->h(pop)->None	h
4	[a,e] -> [a]	None->e(pop)->None	e
5	[a] -> []	None->a(pop)->c	a
6	[] ->[c,f] -> [c]	c->f->f(pop)->None	f
7	[c] -> []	None->c(pop)->g	c
8	[] -> [g] -> []	g-g(pop)->None	g
9	[] -> [], break

然后我们观察发现中序遍历下一节点有以下规律：

节点存在右子树，则下一节点为右子树的左叶子结点，如a, b, c节点。
节点不存在右子树，分两种情况：
1. 该节点是其父节点的左子节点，下一节点为其父节点，如d, f, h节点。
2. 该节点是其父节点的右子节点，那么需要不断向上遍历其父节点，找到一节点node满足node.parent.left == node，那么node.parent是下一节点，如e的下一节点a。

注意，题面并没有告诉二叉树节点有指向其父节点的指针，这里需要与面试官沟通确认。

题解

class Node:
    def __init__(self, val, left=None, right=None, parent=None):
        self.val = val
        self.left = left
        self.right = right
        self.parent = parent

def inorder_next_node(node):
    if not node:
        return None
    
    if node.right:
        # 节点存在右子树
        cur = node.right
        while cur and cur.left:
            cur = cur.left
        return cur
        
    if node.parent:
        # 节点不存在右子树，且存在父节点（根节点不存在父节点）
        if node.parent.left == node:
            return node.parent
        if node.parent.right == node:
            cur = node
            while cur and cur.parent:
                if cur.parent.left == cur:
                    return cur.parent
                cur = cur.parent
    return None

总结

二叉树遍历相关问题考察的是基本功，除了全面理解动手多撸代码之外别无捷径可寻。

最后

欢迎关注个人微信公众号【摸鱼师的博客】！