(2.1) 数值数据的表示
(2.1.3) 原码表示法
(2.1.4) 补码表示法
(2.1.5) 反码表示法
(2.1.6) 3种机器数的比较与转换
(2.2) 机器数的定点表示法与浮点表示
进位计数法

任意进制转十进制

十进制整数数转r进制

十进制小数转r进制

二进制转2*n进制
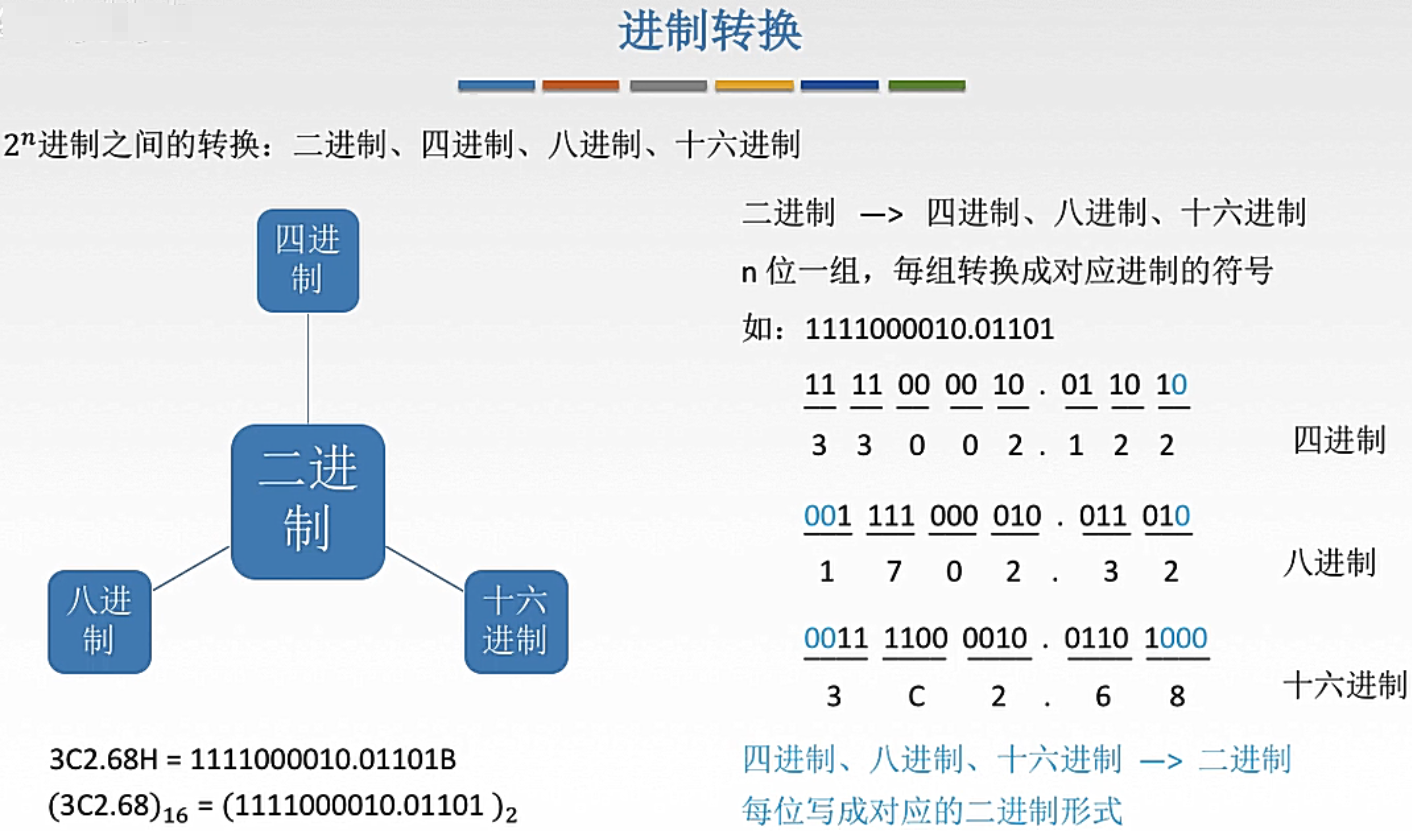
log2R为一组,R为R进制。
(2.2.1) 定点表示法
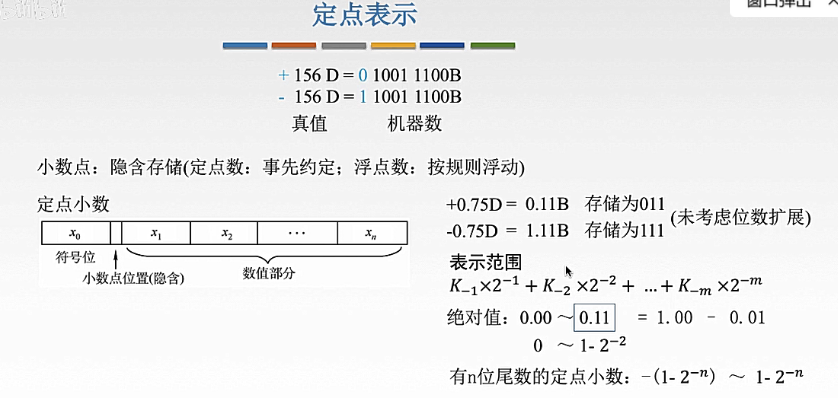
1. 定点小数
2. 定点整数

真值与机器数

总结

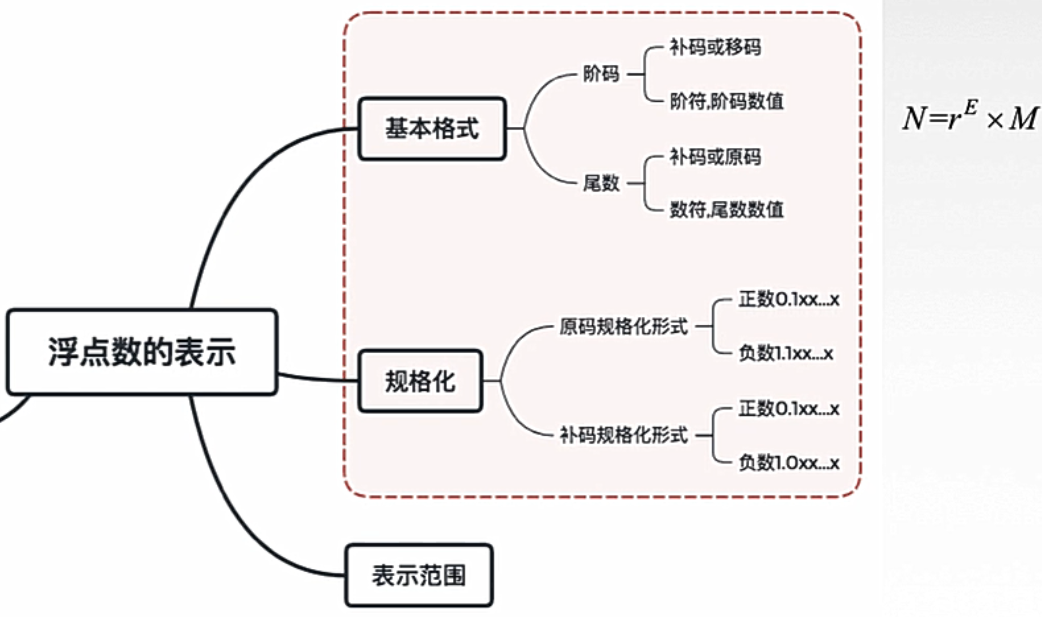
(2.2.2) 浮点表示法
本节总览
浮点数的组成
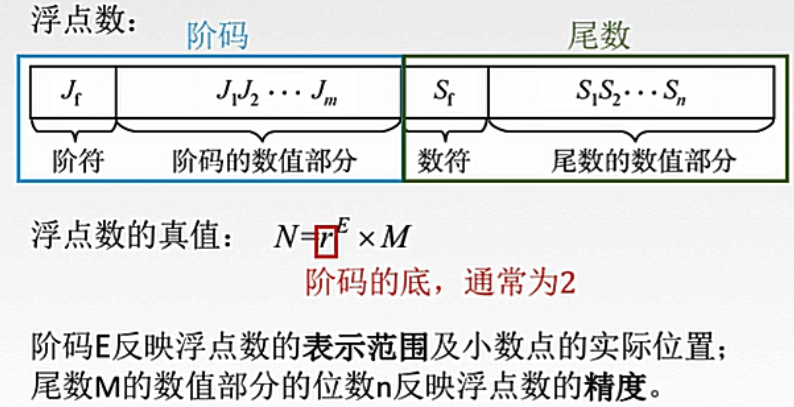
1. 浮点数的表示范围
例题:

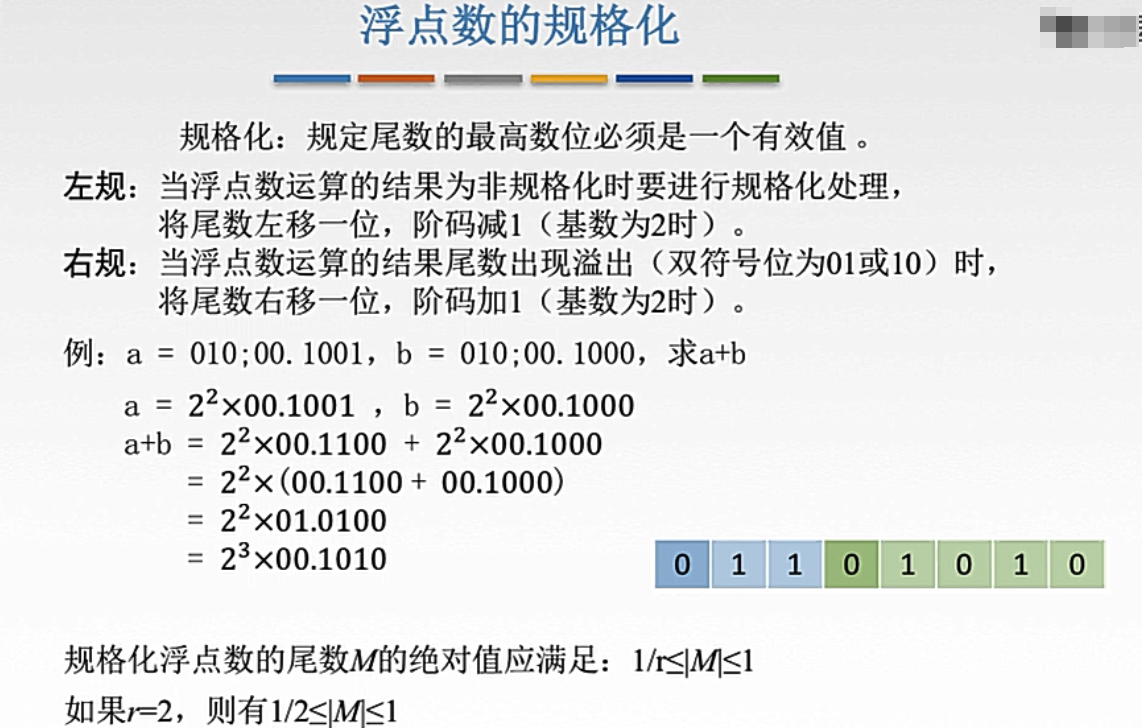
2. 规格化浮点数
规格化:规定尾数的最高位数必须是一个有效值(对二进制来说则是1)。
- 下面的例子就进行了
左规。
浮点数运算产生溢出与左规、右规
原码与补码的规格化

本节总结
(2.3) 非数值数据的表示
(2.3.1) 字符和字符串的表示
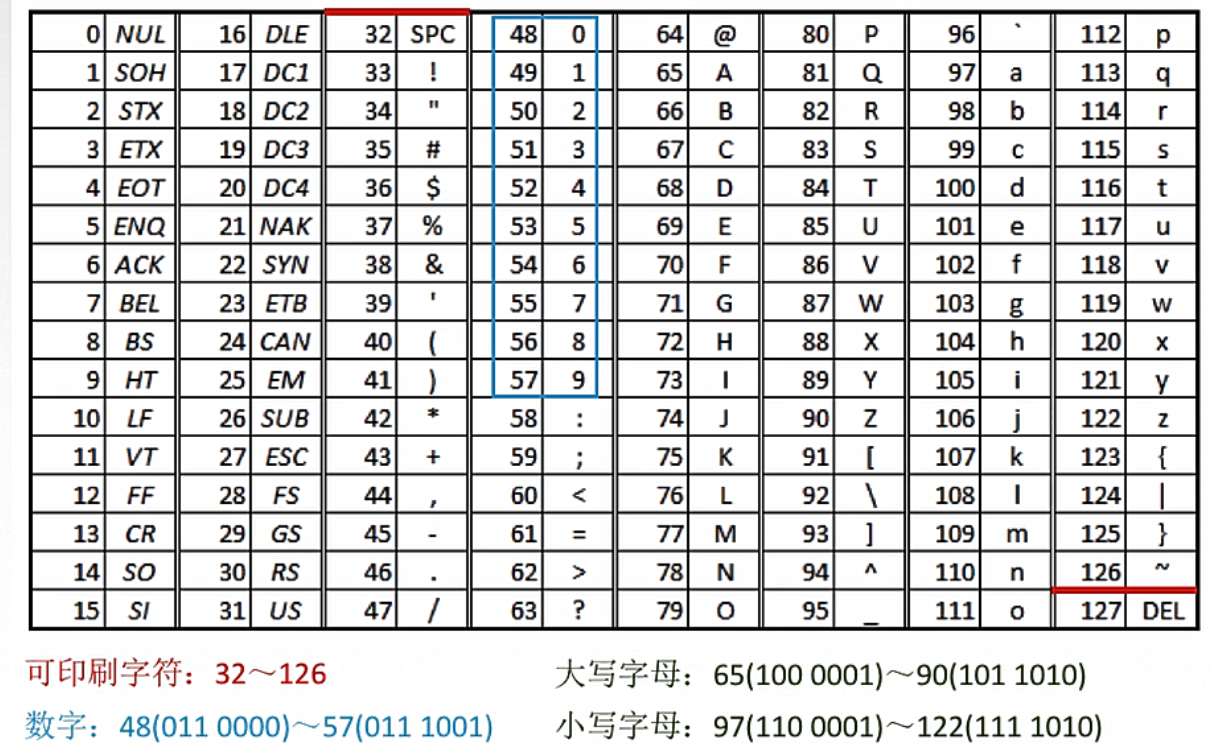
1. ASCII 字符编码
字符和字符串在计算机中如何表示呢?---> ASCII编码。
- 编码:把字符按照一定的规则用一组二进制编码表示。
ASCII编码:是众多编码方式中较流行的一种。
ASCII 码表
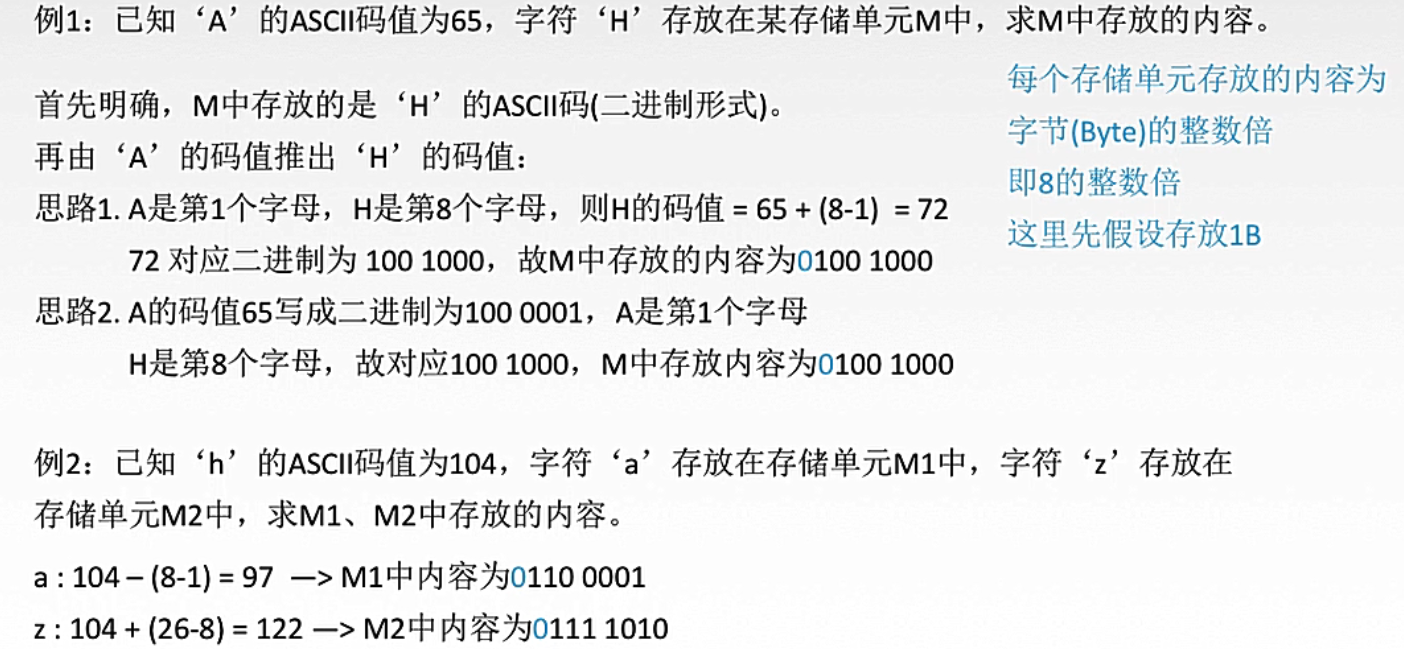
2. 字符串的存放
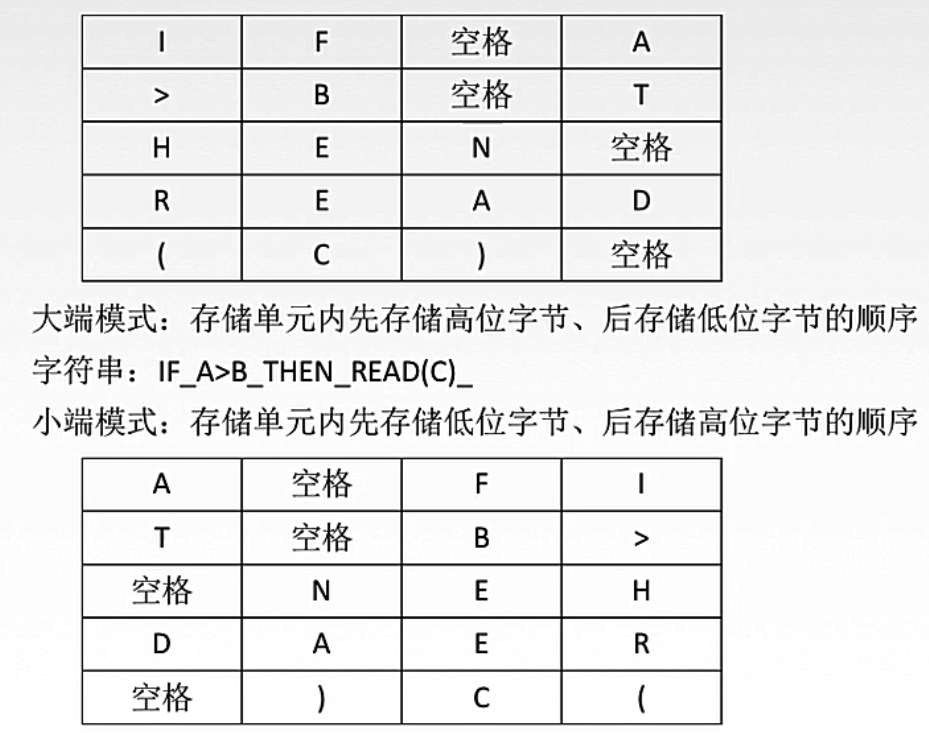
(2.3.1) 汉字的表示
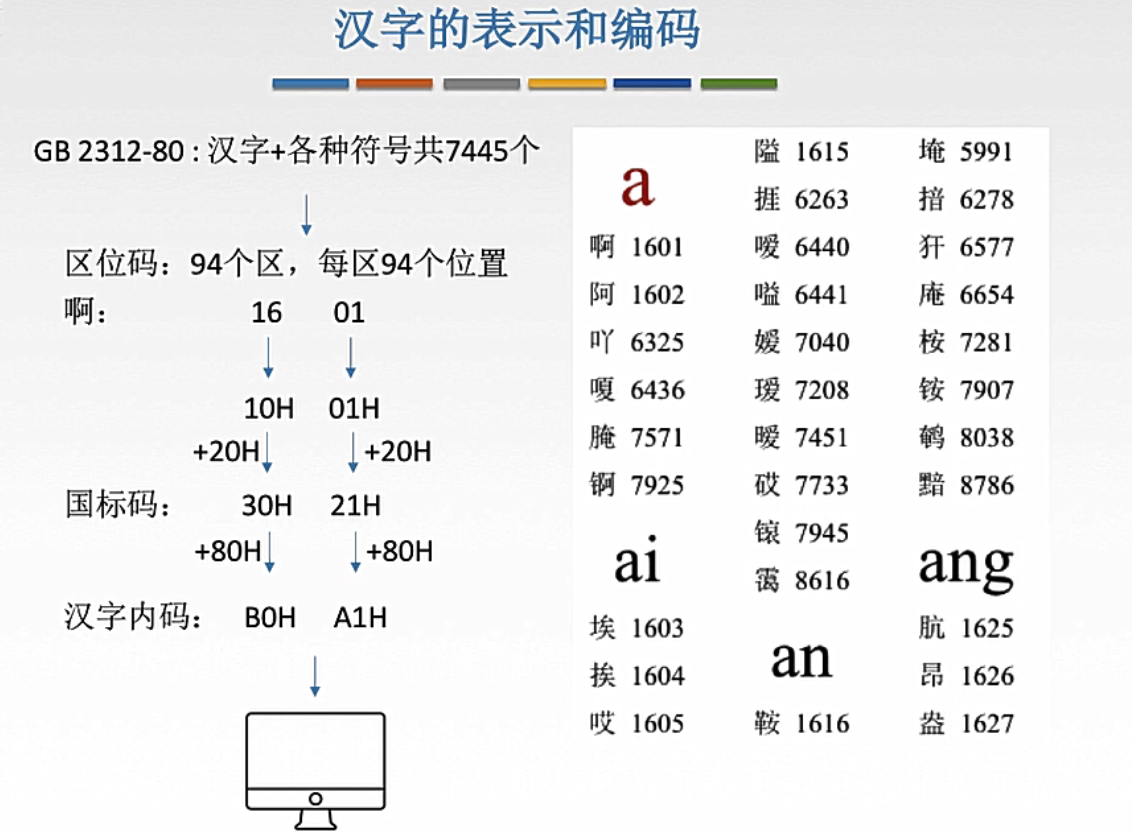
1. 汉字国际码
2, 汉字区位码
3. 汉字机内码
(2.3.1) 统一代码
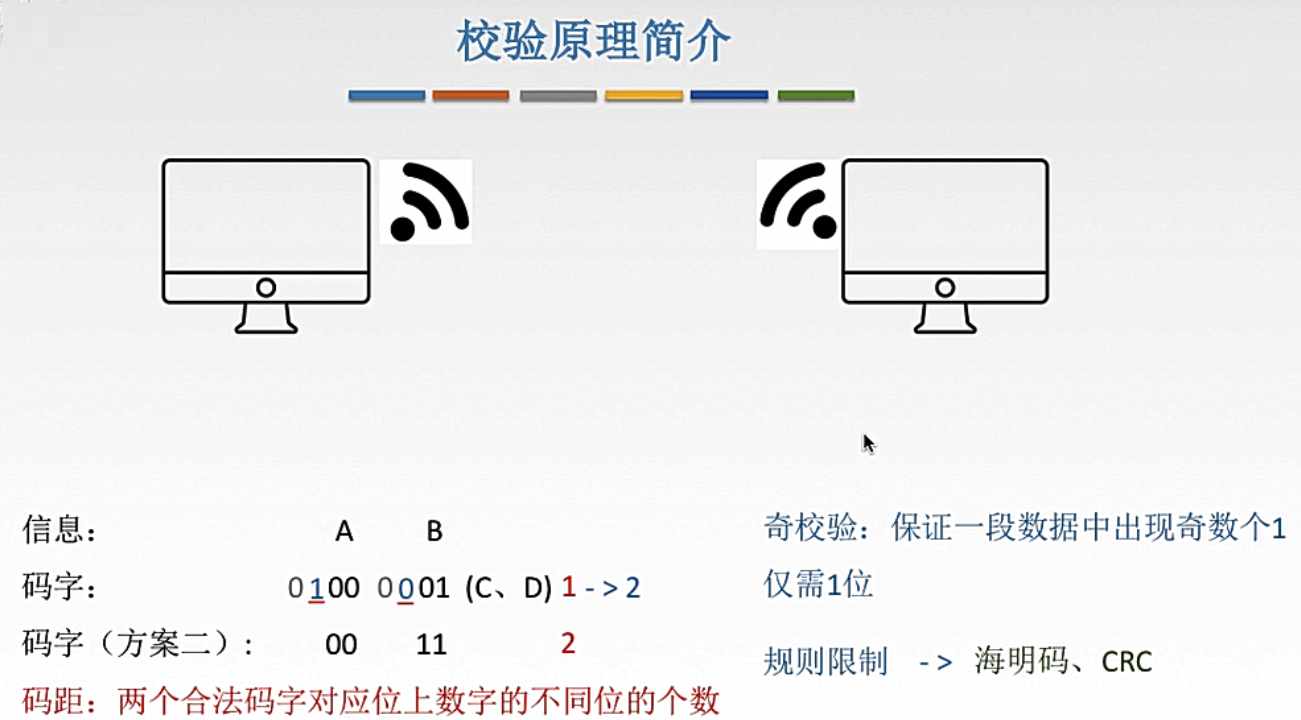
(2.6) 数据校验码
(2.6.1) 奇偶校验码
- 数据校验码:指的是那些能够发现错误或能够自动纠正错误的数据编码。
- 任何一种编码都由码字组成。
- 码距:任意两个码字对应位上的数字的不同位的个数。例如码字
00和11的码距就是2。码距>1的校验码具有差错能力。- 合理增大码距,就能提高发现错误的能力。
1. 奇偶校验概念
2. 简单奇偶校验
例题:

3. 交叉奇偶校验
二、
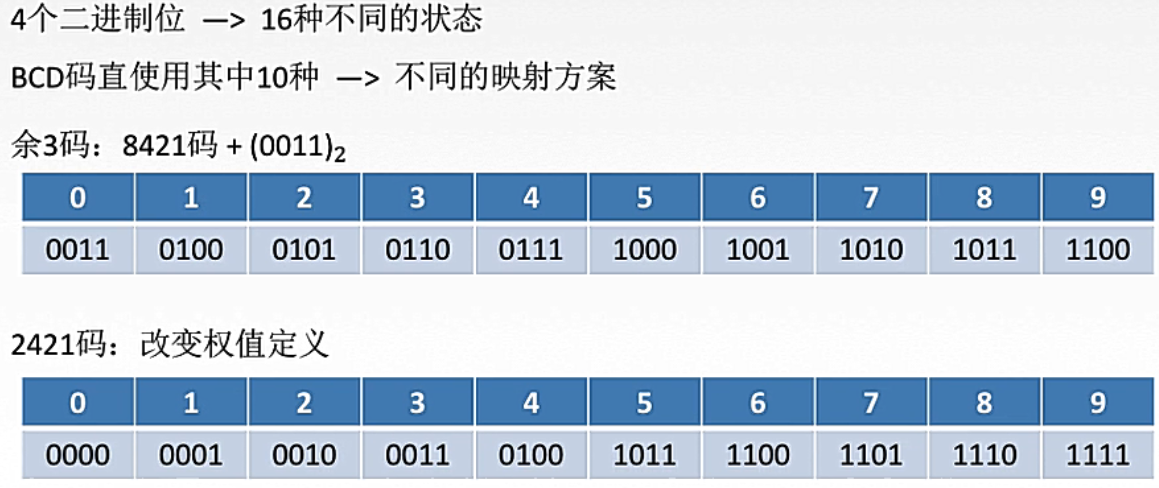
2. 8421码
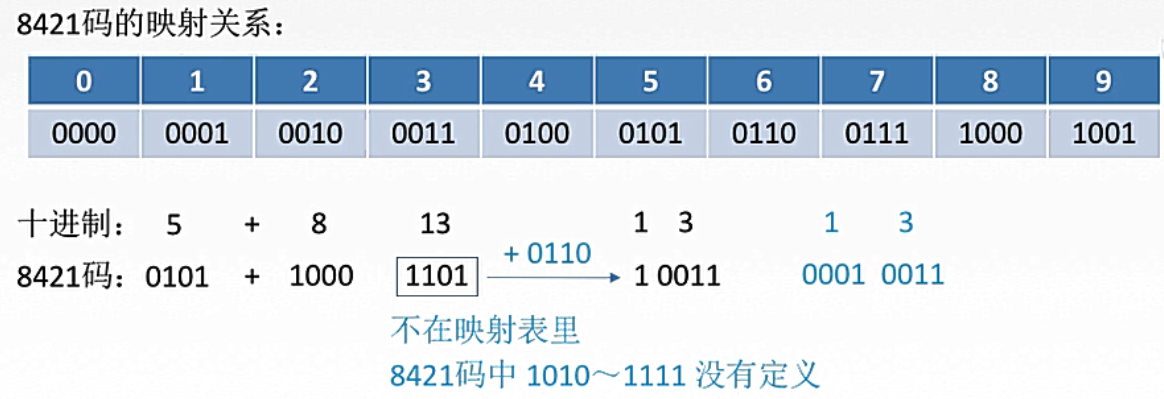
9<x<16时,要加6修正。
余3法和2421法