体系结构Review
二、应用题
1.假定第一种改进措施使用了20%的时间,但提高了2倍的性能;假定第二种改进措施使用了70%的时间,但提高了1.3倍的性能。设旧执行时间为Told,问:使用哪一种改进措施能使执行时间减少最多?
解答:
应用Amdahl定律,针对第一种改进措施有:
新执行的时间=旧执行的时间*((1-0.2)+0.2/2) =0.9旧执行的时间
针对第二种改进措施有:新执行的时间=旧执行的时间*((1-0.7)+0.7/1.3) =0.9旧执行的时间=0.84旧执行的时间
因此使用了第二改进措施后性能提高较小,但它对使用改进措施后的总执行时间影响较大。
2.假定在运行某个程序时,某计算机将90%的时间用于处理某特定计算类型。某制造商进行修改后,使该计算类型的执行速度提高了10倍。问:
(1)当该程序原来的执行时间为100秒,该程序修改以后的执行时间是多少? (2)新旧系统之间的加速比是多少?
解答:
(1)增强比例=0.9,增强加速比=10,则由Amdahl定律的:
新执行的时间=旧执行的时间*((1-增强比例)+ 增强比例/增强加速比) =100*((1-0.9)+0.9/10) =19秒
(2)新旧系统之间的加速比是:加速比=原执行时间/现执行时间=100/19=5.3
3.某台机器的指令集原来进行存储器访问的指令只有Load/Store,其他指令只能在寄存器间操作。这台机器Load/Store指令的使用频率和时钟数如下:
| 操作 | 频率 | CPI |
|---|---|---|
| ALU | 43% | 1 |
| Loads | 21% | 2 |
| Stores | 12% | 2 |
| Branch | 24% | 2 |
现采用优化编译改善其性能,若编译可减少50%的ALU指令,但它不能减少Load、Store、Branch指令,忽略系统因素,并假设时钟周期是20ns(50MHz),问:优化编译后的MIPS和没有优化编译时的MIPS各为多少?MIPS的变化和执行时间的变化是否一致?
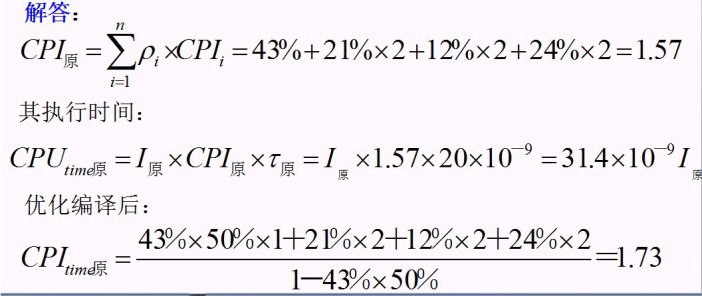

4.考察代码
L.D F6, 34(R2)
L.D F2, 45(R3)
MULT.D F0, F2, F4
SUB.D F8, F6, F2
DIV.D F10, F0, F6
ADD.D F6, F8, F2
假设L.D 可在 1 个时钟周期内完成,CDB需要1个时钟周期把结果送到目的。基于Tomasulo算法进行动态调度,请填写经过12个时钟周期时的保留站 和寄存器状态表:
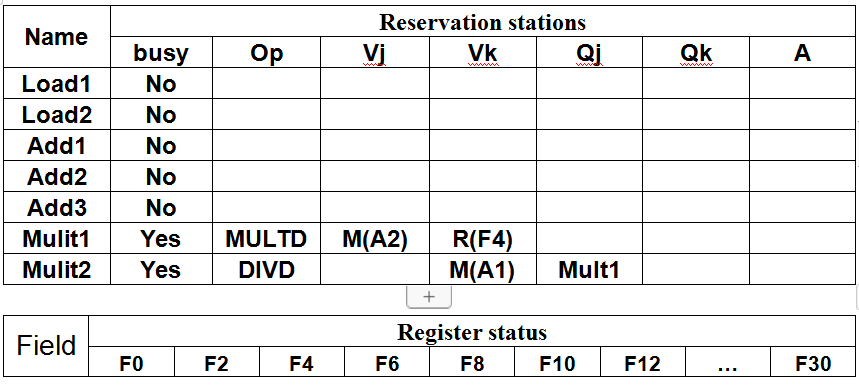
5.代码段,实现序列如下

试用one bit 预测器预测上述代码段的转移行为,将预测结果填下表并给出正确性结论:
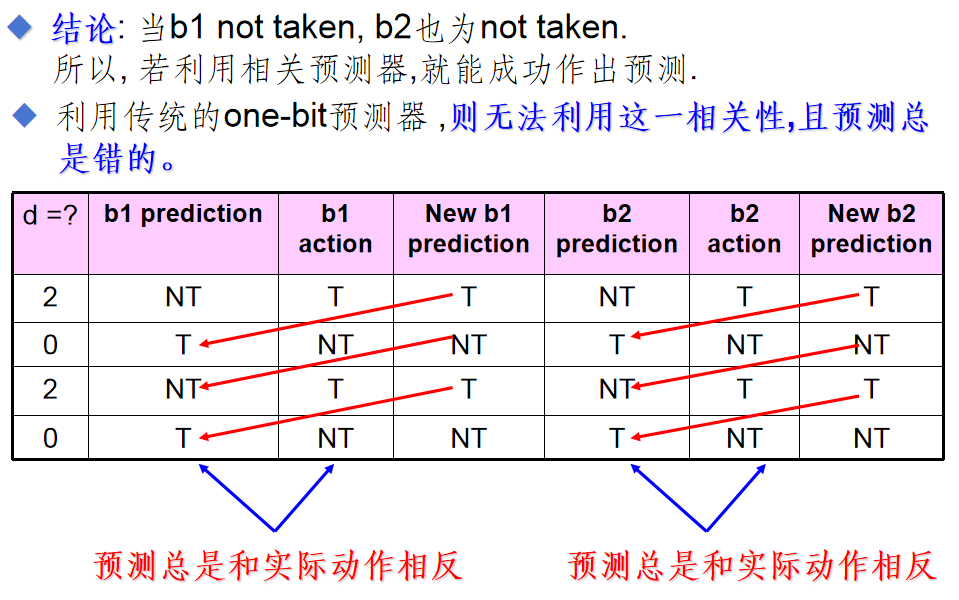
试用2- bit 相关预测器预测上述代码段的转移行为,并给出其正确性结论。
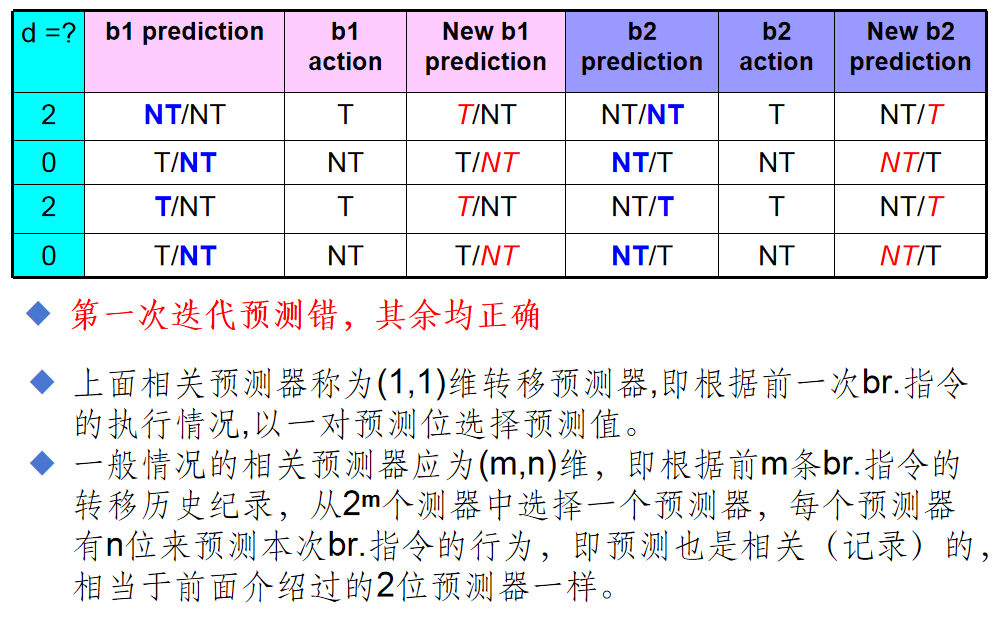
设2-bit相关预测器的第1位是上次转移不成功时的本次预测;第2位是上次转移成功时的本次预测;表中预测初值为NT/NT(下划线表示本次预测),用NT(=branch not taken)和T(=branch taken)表示转移不成功(不发生)和成功(发生)。
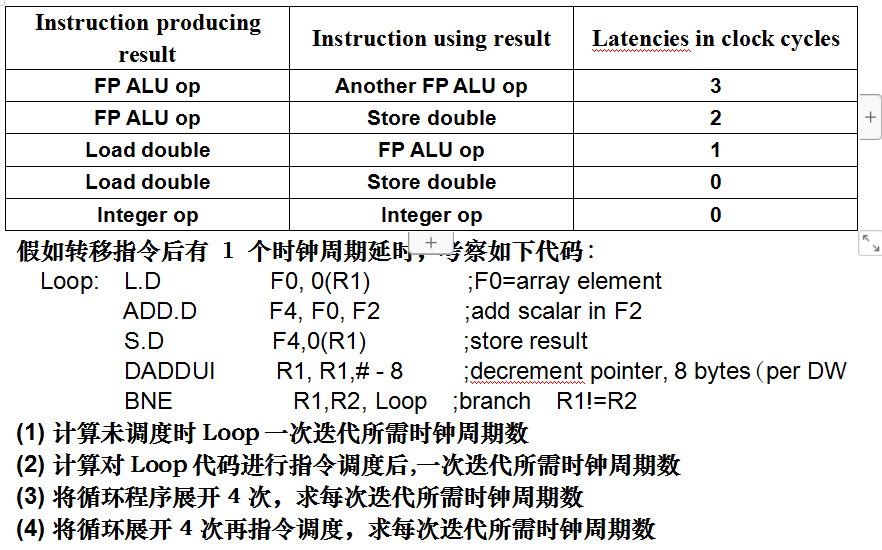
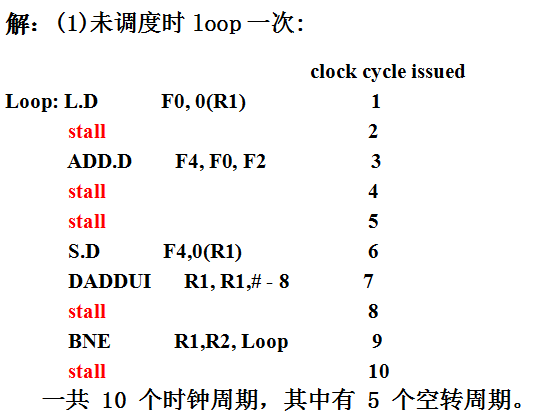
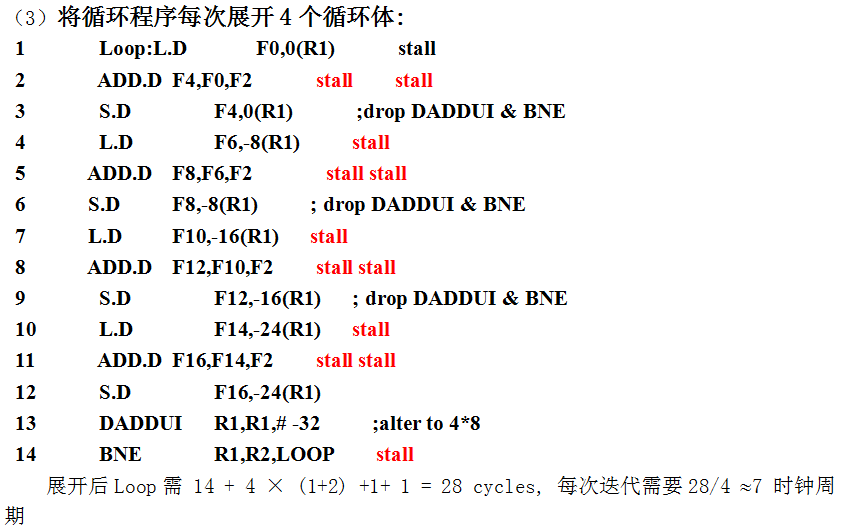
6.FP操作的latencies如下: