经典机器学习算法，他们最本质的区别是分类思想（预测y的表达式）不同，有的是基于概率模型，有的是动态规划，表象的区别就是最后的损失函数不同。

损失函数

损失函数分为经验风险损失函数和结构风险损失函数，经验风险损失函数反映的是预测结果和实际结果之间的差别，结构风险损失函数则是经验风险损失函数加上正则项(L0、L1（Lasso）、L2（Ridge）)。

不同的算法常用的损失函数（Loss Function）有：

一、0-1损失函数（gold standard 标准式）

0-1损失是指，预测值和目标值不相等为1，否则为0：

该损失函数不考虑预测值和真实值的误差程度，也就是说只要预测错误，预测错误差一点和差很多是一样的。感知机就是用的这种损失函数，但是由于相等这个条件太过严格，我们可以放宽条件，即满足 |Y−f(X)|<T时认为相等。

这种损失函数用在实际场景中比较少，更多的是用俩衡量其他损失函数的效果。

二、绝对值损失函数

绝对值损失函数，（暂时还不知道用在啥场合，了解后改正）：

三、平方损失函数（squared loss）

实际结果和观测结果之间差距的平方和，一般用在线性回归中，可以理解为最小二乘法：

四、对数损失函数（logarithmic loss）

主要在逻辑回归中使用，样本预测值和实际值的误差符合高斯分布，使用极大似然估计的方法，取对数得到损失函数：

损失函数L(Y,P(Y|X))L(Y,P(Y|X))是指样本X在分类Y的情况下，使概率P(Y|X)达到最大值。

经典的对数损失函数包括entropy和softmax，一般在做分类问题的时候使用（而回归时多用绝对值损失（拉普拉斯分布时，μ值为中位数）和平方损失（高斯分布时，μ值为均值））。

五、指数损失函数（Exp-Loss）

在boosting算法中比较常见，比如Adaboosting中，标准形式是：

六、铰链损失函数（Hinge Loss）

铰链损失函数主要用在SVM中，Hinge Loss的标准形式为：

y是预测值，在-1到+1之间，t为目标值（-1或+1）。其含义为，y的值在-1和+1之间就可以了，并不鼓励|y|>1|y|>1，即并不鼓励分类器过度自信，让某个正确分类的样本的距离分割线超过1并不会有任何奖励，从而使分类器可以更专注于整体的分类误差。

梯度

梯度下降法快速入门

前言梯度下降法（Gradient Descent）是机器学习中最常用的优化方法之一，常用来求解目标函数的极值。其基本原理非常简单：沿着目标函数梯度下降的方向搜索极小值（也可以沿着梯度上升的方向搜索极大值）。但是如何调整搜索的步长（也叫学习率，Learning Rate）、如何加快收敛速度以及如何防止搜索时发生震荡却是一门值得深究的学问。接下来本文将分析第一个问题：学习率的大小对搜索过程的影响

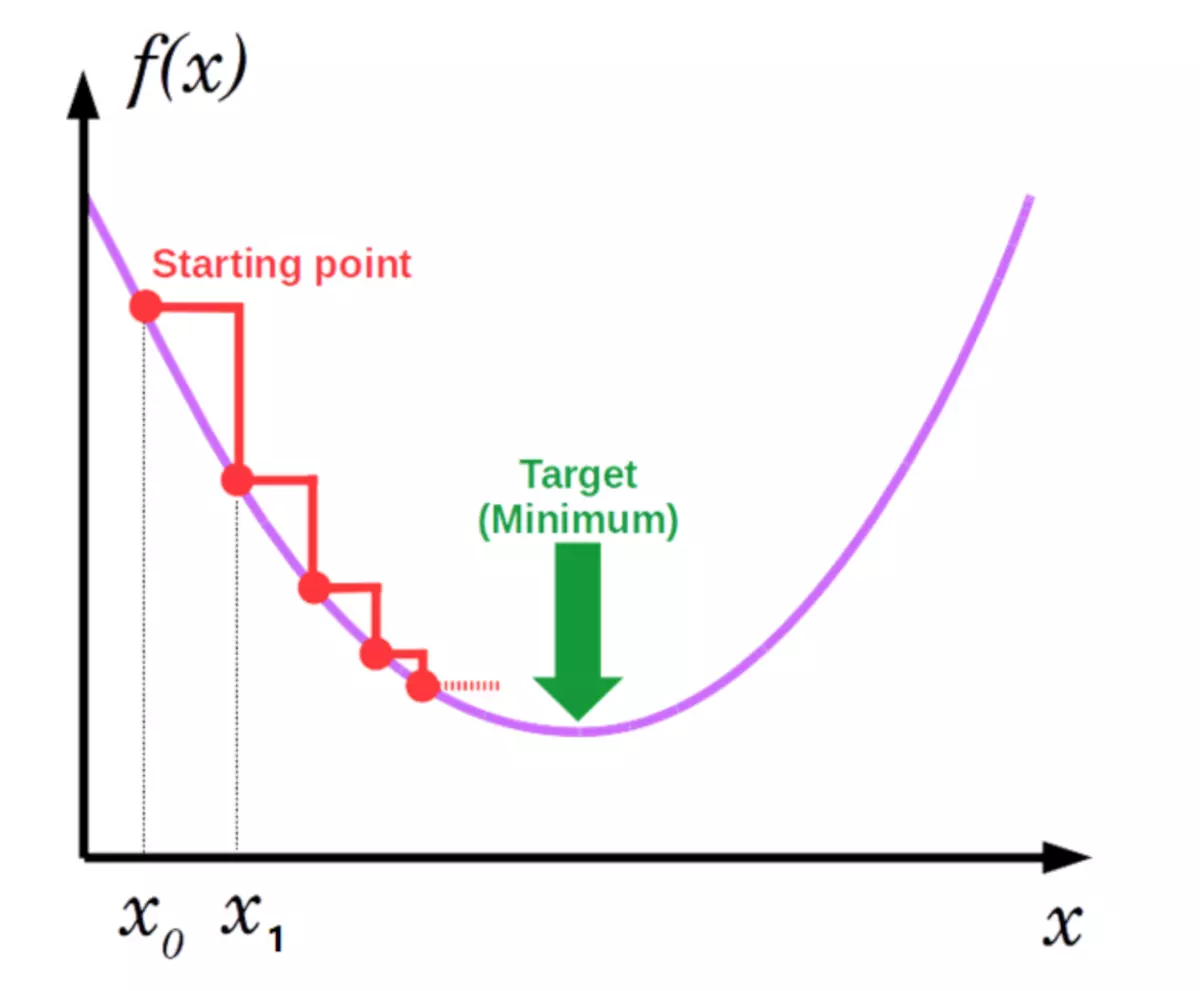
来梳理梯度下降法的原理

梯度下降的相关概念在详细了解梯度下降的算法之前，我们先看看相关的一些概念。

步长（Learning rate）：步长决定了在梯度下降迭代的过程中，每一步沿梯度负方向前进的长度。用上面下山的例子，步长就是在当前这一步所在位置沿着最陡峭最易下山的位置走的那一步的长度。

2.特征（feature）：指的是样本中输入部分，比如2个单特征的样本（x(0),y(0)）,（x(1),y(1)）,则第一个样本特征为x(0)，第一个样本输出为y(0)。

假设函数（hypothesis function）：在监督学习中，为了拟合输入样本，而使用的假设函数，记为hθ(x)。比如对于单个特征的m个样本（x(i),y(i)）(i=1,2,...m),可以采用拟合函数如下： hθ(x)=θ0+θ1x。
损失函数（loss function）：为了评估模型拟合的好坏，通常用损失函数来度量拟合的程度。损失函数极小化，意味着拟合程度最好，对应的模型参数即为最优参数。在线性回归中，损失函数通常为样本输出和假设函数的差取平方。比如对于m个样本（xi,yi）(i=1,2,...m),采用线性回归，损失函数为：
```
  J(θ0,θ1)=∑i=1m(hθ(xi)−yi)2
```

其中xi表示第i个样本特征，yi表示第i个样本对应的输出，hθ(xi)为假设函数。

解决实际问题

是为了解决最优化问题，而最优化问题其实就是我们大学中，来求极大值以及极小值的问题初中时我们就学会了求解二次函数的极值（抛物线的顶点），高中时学习了幂函数，指数函数，对数函数，三角函数，反三角函数等各种类型的函数，求函数极值的题更是频频出现。这些方法都采用了各种各样的技巧，没有一个统一的方案。大学的时候我们使用微积分，而这个就是一个通用的方案:

找到函数的导数等于0的点，因为在极值（请注意极值不一定是全局极值），导数必然为0.

机器学习中，我们一般将最优化问题统一表述为求解函数的极小值问题：

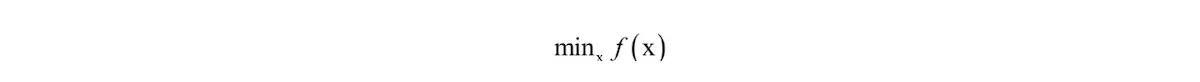
其中x称为优化变量，f称为目标函数。极大值问题可以转换成极小值问题来求解，只需要将目标函数加上负号即可：

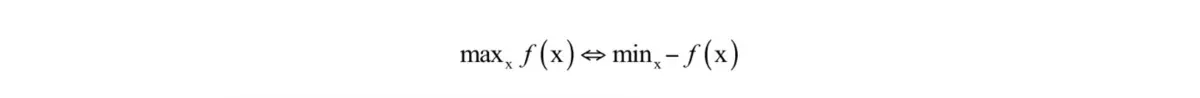
有些时候会对优化变量x有约束，包括等式约束和不等式约束，它们定义了优化变量的可行域，即满足约束条件的点构成的集合。在这里我们先不考虑带约束条件的问题。一个优化问题的全局极小值x是指对于可行域里所有的x，有：

即全局极小值点处的函数值不大于任意一点处的函数值。局部极小值x 定义为存在一个δ邻域，对于在邻域内：

并且在可行域内的所有x，有：

即局部极小值点处的函数值比一个局部返回内所有点的函数值都小。在这里，我们的目标是找到全局极小值。不幸的是，有些函数可能有多个局部极小值点，因此即使找到了导数等于0的所有点，还需要比较这些点处的函数值。

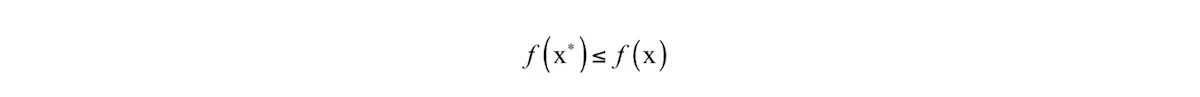
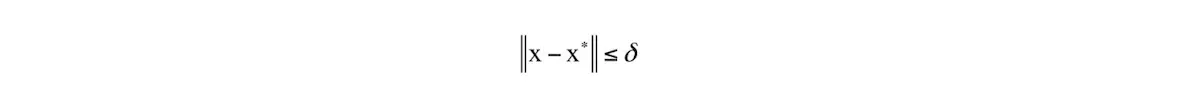
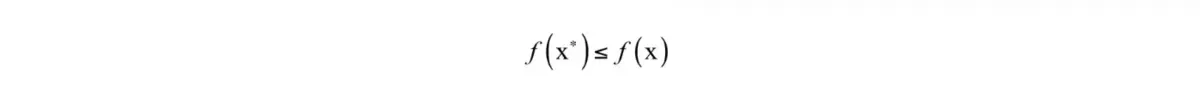
导数与梯度

由于实际应用中一般都是多元函数，因此我们跳过一元函数，直接介绍多元函数的情况。梯度是导数对多元函数的推广，它是多元函数对各个自变量偏导数形成的向量。多元函数的梯度定义为：

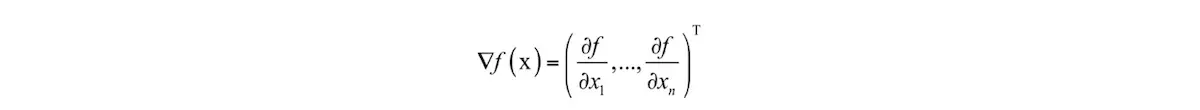
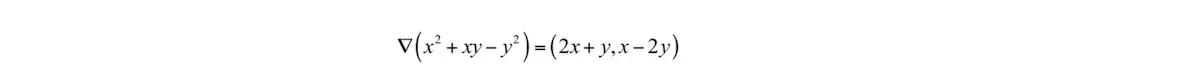
其中∇ 称为梯度算子，它作用于一个多元函数，得到一个向量。下面是计算函数梯度的一个例子：

可导函数在某一点处取得极值的必要条件是梯度为0，梯度为0的点称为函数的驻点，这是疑似极值点。需要注意的是，梯度为0只是函数取极值的必要条件而不是充分条件，即梯度为0的点可能不是极值点。

编写一个梯度下降的例子

首先先假设现在我们需要求解目标函数func(x) = x * x的极小值，由于func是一个凸函数，因此它唯一的极小值同时也是它的最小值，其一阶导函数为dfunc(x) = 2 * x。

import numpy as np

import matplotlib.pyplot as plt

# 目标函数:y=x^2

def func(x): return np.square(x)

# 目标函数一阶导数:dy/dx=2*x

def dfunc(x): return 2 * x

接下来编写梯度下降法函数：

Gradient Descentdef GD(x_start, df, epochs, lr):   
 """    梯度下降法。给定起始点与目标函数的一阶导函数，求在epochs次迭代中x  的更新值    :param x_start: x的起始点    :param df: 目标函数的一阶导函数    :param epochs: 迭代周期    :param lr: 学习率    :return: x在每次迭代后的位置（包括起始点），长度为epochs+1    """    
  xs = np.zeros(epochs+1)    
  x = x_start    
  xs[0] = x    
  for i in range(epochs):        
    dx = df(x)        
  # v表示x要改变的幅度        
  v = - dx * lr       
  x += v        
  xs[i+1] = x
  return xs

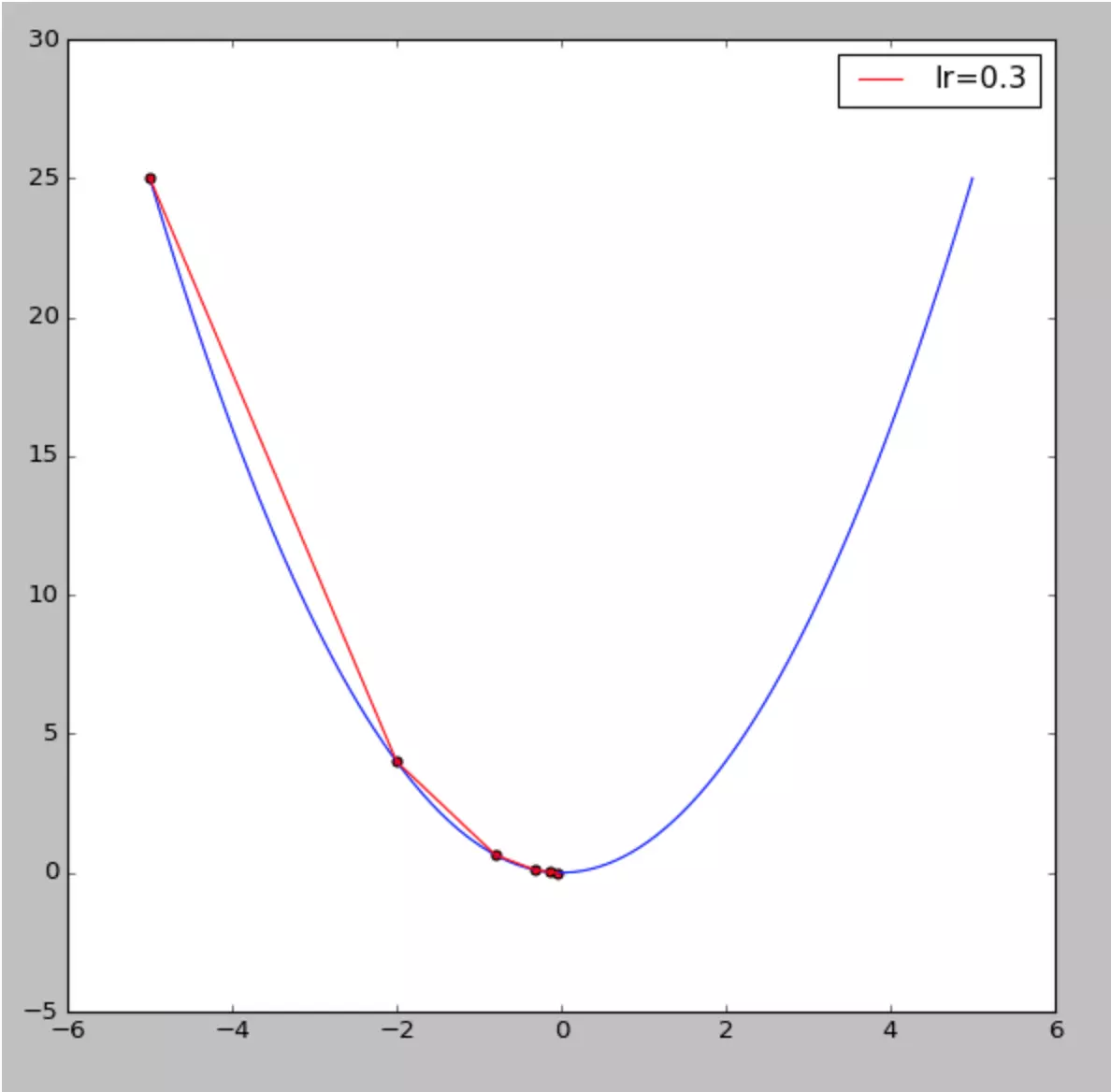
需要注意的是参数df是一个函数指针，即需要传进我们的目标函数一阶导函数。测试代码如下，假设起始搜索点为-5，迭代周期为5，学习率为0.3：

def demo0_GD():    
"""演示如何使用梯度下降法GD()"""    
  line_x = np.linspace(-5, 5, 100)   
  line_y = func(line_x)    
  x_start = -5    
  epochs = 5    
  lr = 0.3    
  x = GD(x_start, dfunc, epochs, lr=lr)    
  color = 'r'    
  plt.plot(line_x, line_y, c='b')    
  plt.plot(x, func(x), c=color, label='lr={}'.format(lr))    
  plt.scatter(x, func(x), c=color, )    
  plt.legend()

  plt.show()

学习率对梯度下降法的影响

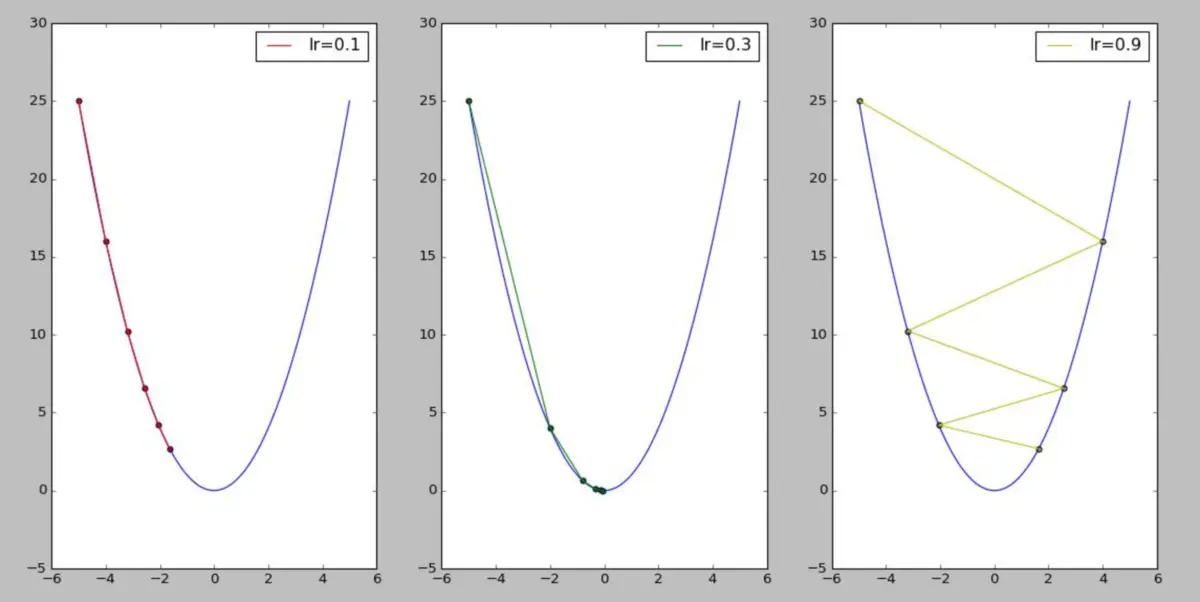
在上节代码的基础上编写新的测试代码demo1_GD_lr，设置学习率分别为0.1、0.3与0.9：

def demo1_GD_lr():    
  # 函数图像   
  line_x = np.linspace(-5, 5, 100)    
  line_y = func(line_x)    
  plt.figure('Gradient Desent: Learning Rate')    
  x_start = -5    
  epochs = 5    
  lr = [0.1, 0.3, 0.9]    
  color = ['r', 'g', 'y']    
  size = np.ones(epochs+1) * 10    
  size[-1] = 70    
  for i in range(len(lr)):        
  x = GD(x_start, dfunc, epochs, lr=lr[i])        
  plt.subplot(1, 3, i+1)        

  plt.plot(line_x, line_y, c='b')        
  plt.plot(x, func(x), c=color[i], label='lr={}'.format(lr[i]))        
  plt.scatter(x, func(x), c=color[i])        
  plt.legend()

  plt.show()

从下图输出结果可以看出两点，在迭代周期不变的情况下：

学习率较小时，收敛到正确结果的速度较慢。学习率较大时，容易在搜索过程中发生震荡。

决策边界

logistic回归虽然带着回归两字却和线性回归有很大的区别，线性回归主要用于预测问题，其输出值为连续变量，而logistic回归主要用于分类问题，其输出值为离散值。logistic回归可以用于多元分类问题，也可以用于二元分类问题，但二元分类更为常用。因此本文只介绍二元分类的应用。

先来看一些logistic回归的基本东西，logistic回归的假设函数为：

，因为

.因此

。

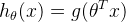
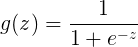
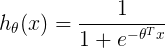
其中

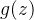
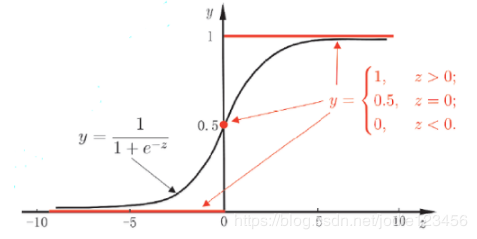
称为S型函数（sigmoid function)或者逻辑函数(logistic function)，其函数图像如图所示：

从函数图像中很容易观察出

，即

。

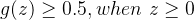
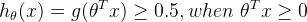
举个例子:对于肿瘤数据集，假设其中一个特征为肿瘤的尺寸，结果为{恶性，良性}。假设

即肿瘤为恶性的概率为0.7，因此

,即在给定

的条件下y=1的概率。对于二元分类问题，

。

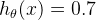
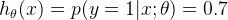
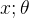
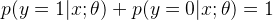
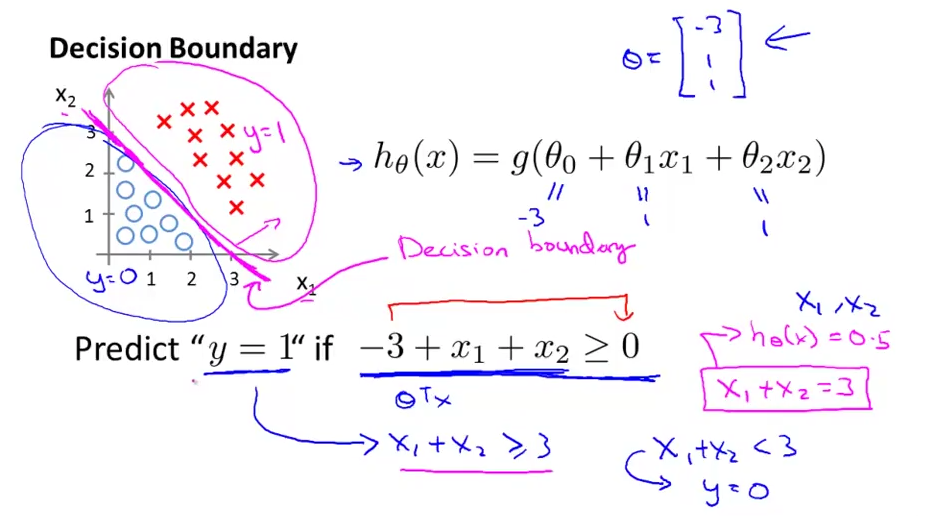
下面来说一下决策边界问题，下面介绍决策边界(decision boundary)，所谓决策边界就是能够把样本正确分类的一条边界，主要有线性决策边界(linear decision boundaries)和非线性决策边界(non-linear decision boundaries)。注意：决策边界是假设函数的属性，由参数决定，而不是由数据集的特征决定。下面主要举一些例子，形象化的来说明线性决策边界和非线性决策边界。先看一个线性决策边界的例子；下面是在机器学习课上的一个例子

下面来看一下非线性的决策边界的例子：

机器学习-逻辑回归