背景
面试中被问到如何检测链表中是否有环的问题,刷过 Leetcode 或者看过剑指 offer 的同学都知道,这道题是属于快慢指针的应用,这道题的引申问题是通常设置快指针的速度是慢指针2倍,那如果是3倍呢、4倍...N倍呢,是否仍能满足检测有环?或者问是否快慢指针在任一条件下都能够用来检测链表的环呢?带着这样的问题,就有了本文的内容
快慢指针检测是否有环的数学原理
假设链表有环,快指针比慢指针走得快,链表总长度为 a,环长度为 b,快指针每次走 x步,慢指针每次走 y步,又假设链表头距离环入口位置距离为 L1,当慢指针走到环入口位置时,快指针在链表中的位置距离环入口的长度为 L2:
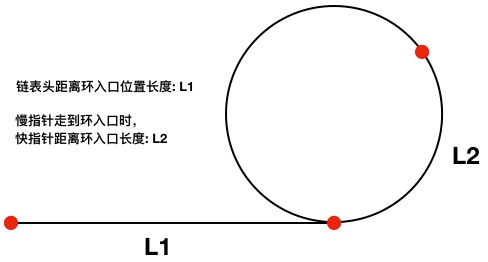
dF = L1 + L2 + N * b,N为快指针在环内可能走过的圈数
dS = L1
之后,假设经过了 i 步,快慢指针在环中相遇:
dF - L1 + x * i ≡ (dS - L1 + y * i) mod b
=> L2 + N * b + x * i ≡ (y * i) mod b
=>
L2 + (x - y)* i ≡ 0 mod b=>(x-y)* i ≡ L2 mod b ----(1)
之所以用取模运算是以为快慢指针在环内的运动是追及问题,随着时间的增长,二者在环内多次相遇是一定的,从上面红色推导等式中也可以得出此结论,因为L2 为正整数, x - y 也为正整数,所以一定存在 L2 +(x -y)*i 满足整除环长b的情况。
同时若存在这样的 i,上述问题就转变为线性同余方程①的求解问题。
线性同余方程
形如ax≡c mod b 的方程称为线性同余方程,其有解的的情况是 当且仅当 c 能够被 a和 b的最大公约数整除,求解线性同余方程通常会用到**裴蜀定理, 即给定两个整数 a, b,必存在整数 x,y使得 ax+by = gcd(a, b),即 a和 b的最大公约数。**裴蜀定理有解时必然有无穷多个整数解,要证明这个定理又涉及到了辗转相除法(欧几里得算法)下面举例说明裴蜀定理,已知12 和 42的最大公约数是 6,则方程 12x+42y=6有解,可以找到
-3 * 12 + 1 * 42 = 6
4 * 12 + (-1) * 42 = 6
对于线性同余方程 ax≡c mod b, 若 d = gcd(a, b)能够被 c整除,由裴蜀定理,存在整数对(r, s),使得
a * r + b * s = d,因此有
x = r * b / d 是线性同余方程 ax≡c mod b的一个特解,其通项可以表示为
x = { r * c / d + k * b / d | k属于整数}
那如何求这个特解 r 呢?
由上面结论我们知道线性同余方程的等价方程:
a * x + b * y = gcd(a, b)-------(2)
假设 x1 和 y1 是在x的系数为 b % a,y的系数为 a 情况一下的一个解,于是有:
(b%a) * x1 + a * y1 = gcd(a, b) -------(3)
根据除法原理,余数 = 被除数 - 商 * 除数,于是我们知道 b % a = b - ⌊b / a⌋ * a,⌊b/a⌋代表 b 除以 a的向下取整,带入方程(3)得到:
(b - ⌊b/a⌋ * a) * x1 + a * y1 = gcd(a, b)
=> b * x1 + a * (y1 - (⌊b/a⌋) * x1) = gcd(a, b) -----(4)
解方程(2)和方程(4)的二元一次方程组得到:
x = y1 - ⌊b / a⌋ * x1
y = x1
以上就特解的求解方法,也是欧几里得扩展算法应用。
快慢指针的速度差在什么条件下能够用于检测环?
由方程(1)我们知道快慢指针检测环的问题实质是求线性同余方程(x-y)* i ≡ L2 mod b解的问题,即当gcd(x-y, b) 能够被L2整除时,线性同余方程有解。进而推导出一定有解的条件是 x- y 与 b互质,即二者的最大公约数为 1,一定可以被 L2 整除。所以也就有了快慢指针速度差和环长互质的结论,但互质是充分条件,而非必要条件,下面举例说明:
当 x = 2, y = 1, b = 4, L2 = 2 => gcd(2 - 1, 4) = 1,能够被 L2整除,满足条件
当 x = 3, y = 1, b = 4, L2 = 2 => gcd(3 - 1, 4) = 2,能够被 L2整除,虽满足条件,但不是互质
当 x = 4, y = 1, b = 4, L2 = 2 => gcd(4 - 1, 4) = 1,能够被 L2整除,满足条件
当 x = 5, y = 1, b = 4, L2 = 2 => gcd(5 - 1, 4) = 4, 不能够被 L2整除,不满足条件
当 x = 6, y = 1, b = 4, L2 = 2 => gcd(6 - 1, 4) = 1,能够被 L2整除,满足条件
....
由此可以看出,快慢指针的速度比并非任意倍数都满足,仅在快慢指针速度差和环长互质的情况下一定可以用于检测是否有环,非互质的条件下,只有特殊情况才满足。
代码实现
一般检测链表中是否有环直接用快慢指针迭代就可以了,winter老师给了一道这种题的变体,如果链表很长,达到数十亿的规模,还是上述已知条件,链表长度为 a,环长度为 b,快指针速度为 x,慢指针速度为 y,什么时候能够相遇?不能用迭代
如果不能用迭代,那可以考虑利用通项来求解。通过上面的数学推论我们知道,相遇位置假设 d = gcd(x - y, b),则通项 i = r * L2 / d + k * b / d
k 为任意整数,取值范围从 0...d -1,所以最终也就转化为求限定条件下 i 的序列的问题
let gcd = function(l, r) {
if (!r) { //0与任何其他整数取最大公约数都是那个数本身
return l
}
return gcd(r, l % r)
}
//欧几里得扩展算法
let gcd_special = function(a, b) {
if (!a) {
return [0, 1]
} else {
let [x1, y1] = gcd_special(b, a % b)
let x = y1 - Math.floor(b/a) * x1
let y = x1
return [x, y]
}
}
//(x-y)*i=L2(mod b)
let position = function(k, circleLen, fastSpeed, slowSpeed, L2) {
let [r, s] = gcd_special(fastSpeed-slowSpeed, circleLen)
let d = gcd(fastSpeed-slowSpeed, circleLen)
if (L2 % d !== 0) return null;
return r * L2 / d + k * circleLen / d
}