算法对于程序员的要求是相当的严格,下面咱们就来聊聊面试最常见的算法吧!!!
1.线性查找算法
此算法为一般查找算法,时间复杂度为n,后期可以通过二分法查找算法优化
示例代码:
package com.yueqian.shujujiegou;
import javax.swing.plaf.FontUIResource;
/**
* 数据结构------------线性查找算法
* @author LinChi
*
*/
public class Select_SuanFa {
public static void main(String[] args) {
//目标数组
int[] arr = new int[] {1,2,3,4,5,6,7,8,9};
//目标元素
int target = 7;
//元素下标
int index = -1;
//循环遍历
for(int i = 0;i<arr.length;i++) {
if(arr[i] == target) {
index = i;
break;
}
}
System.out.println("查找到"+target+"元素的下标:"+index);
}
}
2、二分法查找算法
最坏情况时间复杂度为 O(log2n)
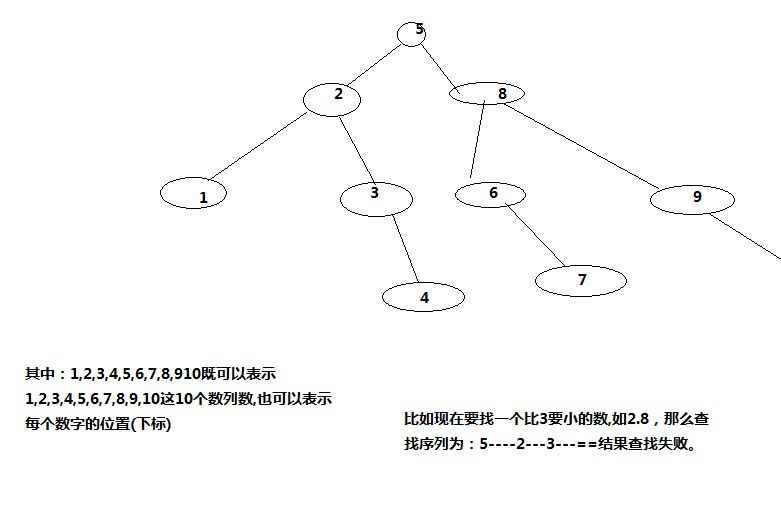
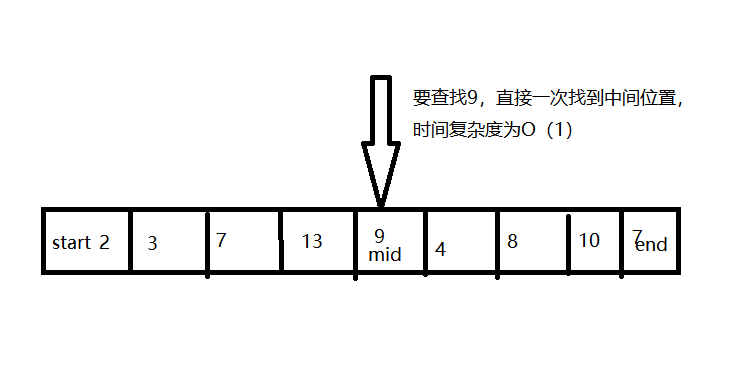
设置开始位置start,结束位置end,以及中间位置 mid=(end+start)/2,
如果arr[index]=mid,返回mid
如果arr[index]>mid,从后半段查找,将start设置为mid+1
如果arr[index]<mid,从后半段查找,将end设置为mid-1
如果start>end,返回-1,说明所查元素不存在
完整代码:
package com.yueqian.shujujiegou;
import java.util.Arrays;
/**
* 数据结构---------二分法查找
* @author LinChi
*
*/
public class Select1_SuanFa2 {
public static void main(String[] args) {
System.out.println(select(44));
}
public static int select(int target) {
//定义数组
int[] arr = {21,32,36,44,45,36,47,38,29};
//定义初始位置
int start = 0;
//定义结束位置
int end = arr.length-1;
//定义中间位置
int mid = (start+end)/2;
while(true) {
//如果没有这个元素,则start>=end,返回-1
if(start>end) {
return -1;
}
//判断是否和中间位置元素值相等
if(arr[mid] == target) {
//将中间位置的索引赋值给目标位置
return mid;
}else {
if(arr[mid] > target) {
//将end位置设置为中间位置减一
end = mid-1;
}else {
//将start位置设置为中间位置加1
start = mid+1;
}
//取出新的中间位置(别忘记了)
mid = (start+end)/2;
}
}
}
}
3、递归算法
斐波那契数列 :0 1 1 2 3 5 8 13 21 ... n
递归实现
//递归实现 (时间复杂度为 2的n次方) n比较大时耗时太长
public static int diGui(int n) {
//先判断是否为0或1
if(n <= 2) {
return 1;
}else {
return diGui(n-2)+diGui(n-1);
}
}
for循环优化实现
//使用for循环优化这个递归 (时间复杂度为n) 此算法性能比递归算法性能高很多
public static int xunHuan(int n) {
//定义第一个数
int first = 0;
//定义第二个数
int second = 1;
for(int i = 0;i<n-1;i++) {
//替换操作
int sum = first+second;
first = second;
second = sum;
}
return second;
}
面试题: 有一对兔子,从出生后第三个月起,每个月都生一对兔子,小兔子长到3个月后,又生一对兔子,假如兔子都不死,问第7个月总共有多少对兔子?
1月 2月 3月 4月 5月 6月 7月
1对 1对 2对 3对 5对 8对 13对(斐波那契数列)
递归实现(时间复杂度为2的N次方)
//生兔子问题
public int birthRabbit(int month){
if(month == 1 || month == 2) {
return 1;
} else {
return birthRabbit(month - 1) + birthRabbit(month - 2);
}
}
for循环优化(时间复杂度为N)
//使用for循环遍历
public static int add1(int n) {
//定义第一个数
int first = 1;
int second = 1;
for(int i = 1;i<n-1;i++) {
int sum = first+second;
first = second;
second = sum;
}
return second;
}
面试题: 在你面前有一个n阶的楼梯,你一步只能上1阶或2阶。请问,当N=11时,你可以采用多少种不同的方式爬完这个楼梯

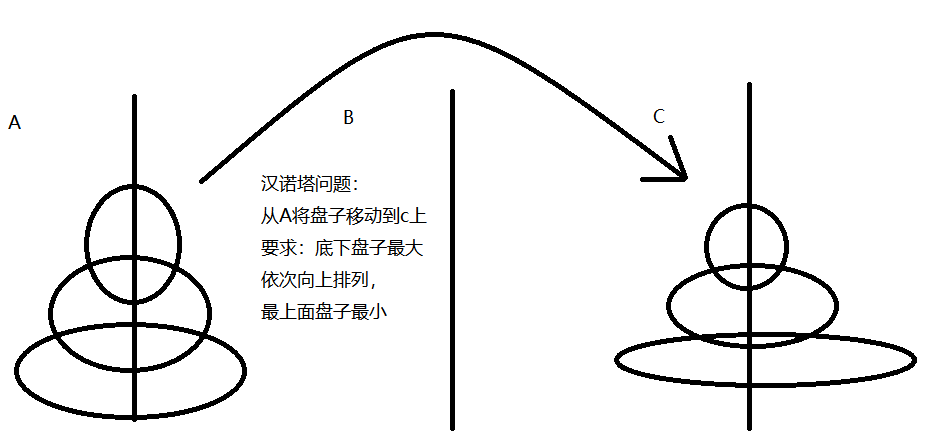
package com.yueqian.shujujiegou;
/**
* 数据结构------递归算法----汉诺塔问题
* @author LinChi
*
*/
public class DiGui_HanNuoTa {
public static void main(String[] args) {
hanNuoTa(3, 'A', 'B', 'C');
}
/**
*
* @param n 总共的盘子数
* @param from 开始移动的柱子
* @param in 中间的柱子
* @param to 目标的柱子
* 无论多少个盘子,都认为只有两个,上面的所有盘子,和下面最大的一个盘子
*/
public static void hanNuoTa(int n,char from,char in,char to) {
if(n==1) {
System.out.println("第1个盘子从"+from+"移动到"+to);
}else {
//移动上面所有的盘子到中间位置
hanNuoTa(n-1,from,to,in);
//移动下面最大的盘子
System.out.println("第"+n+"个盘子从"+from+"移动到"+to);
//将上面所有的盘子从中间位置移动到目标位置
hanNuoTa(n-1,in,from,to);
}
}
}
敲黑板
面对以上的几种数据结构算法问题,小伙伴们考虑下这些算法实现的思想,将复杂问题简单化,寻找规律,拓宽思维,方能解出思路。
推荐自己的github地址:github.com/Lmobject
小可爱们,java实现查找算法,递归算法到此就介绍完了,对二叉树感兴趣的可以加关注哦!!!,后期持续更新中。。。。