冒泡
无序数组经过冒泡排序后,可变成由小到大的有序数组
这里,我的实现思路是先把数组中最小的数字冒到最前面,然后第二小的冒到前面第二个位置。

function bubble(arr) {
var l = arr.length;
for (var i = 0; i < l; i++) {
for (var j = l - 1; j > i; j--) { // 从最后一个数字开始
if (arr[j] < arr[j - 1]) { // 如果当前数字比前面的小,那就把当前数字排在前面
var temp = arr[j];
arr[j] = arr[j - 1];
arr[j - 1] = temp;
}
}
}
return arr;
}
console.log(bubble([100,3,44,1,5,2,50,9,6])) // [1, 2, 3, 5, 6, 9, 44, 50, 100]另外,常见的算法是像下面这样实现的,这种实现更像是沉底,而不像冒泡。

function bubbleSort(arr) {
var len = arr.length;
for (var i = 0; i < len - 1; i++) {
for (var j = 0; j < len - 1 - i; j++) {
if (arr[j] > arr[j+1]) { // 相邻元素两两对比
var temp = arr[j+1]; // 元素交换
arr[j+1] = arr[j];
arr[j] = temp;
}
}
}
return arr;
}快速排序
1.在数组中选择一个元素作为基准点;
2.所有比基准值小的元素摆放在左边,而大于基准值的摆放在右边;
3.最后利用递归,将摆放在左边的数组和右边的数组重复进行上述的1和2操作。
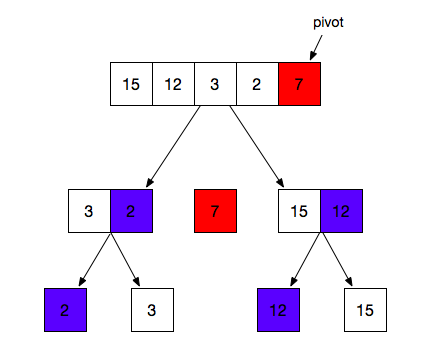
function quickSort(arr) {
if (arr.length <= 1) {
return arr;
}
var pivotIndex = Math.floor(arr.length / 2);
var pivot = arr.splice(pivotIndex, 1)[0];
var left = [];
var right = [];
for (var i = 0; i < arr.length; i++) {
if (arr[i] < pivot) {
left.push(arr[i]);
} else {
right.push(arr[i]);
}
}
return quickSort(left).concat([pivot], quickSort(right))
}
quickSort([12,3,7,4,5,1,89]) // [1, 3, 4, 5, 7, 12, 89]
二分查找
在一个无序数组中,找到一个值的位置索引,采用二分查找,每次可缩小一半的查找范围
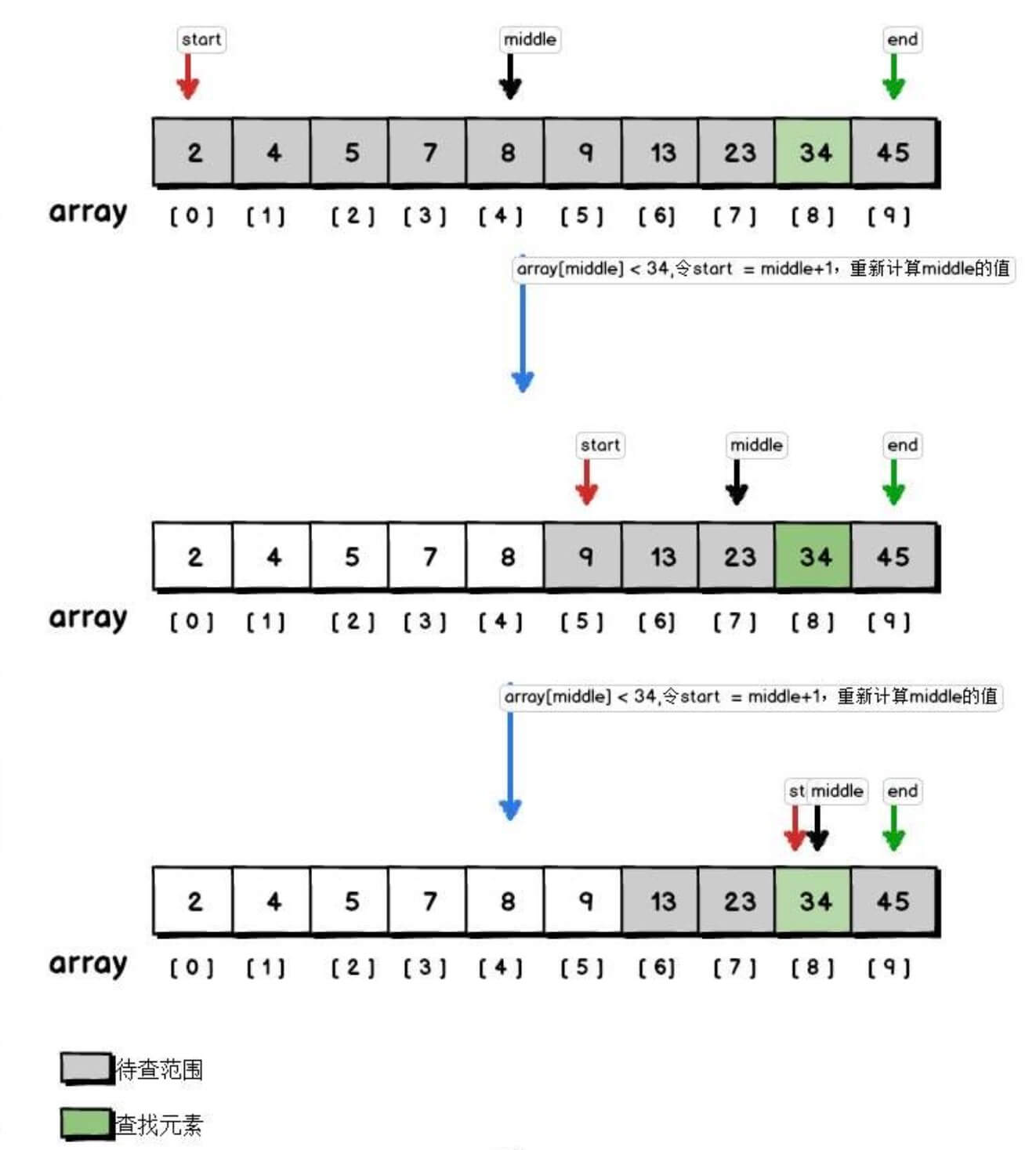
function binarySearch(arr, target) {
var start = 0;
var end = arr.length - 1;
var mid;
while (start <= end) {
mid = Math.floor((start + end) / 2);
if (target === arr[mid]) {
return mid;
} else if (target < arr[mid]) {
end = mid - 1;
} else {
start = mid + 1;
}
}
}
var arr = [2,4,5,7,8,9,13,23,34,45]
binarySearch(arr, 34) // 8以上是通过while循环+start和end缩减范围实现的,还有一种递归的实现方式, 如下
function binarySearch(arr, target, start, end) {
var start = start || 0;
var end = end || arr.length - 1;
var mid = Math.floor((start + end) / 2);
if (target === arr[mid]) {
return mid;
} else if (target > arr[mid]) {
return binarySearch(arr, target, mid + 1, end);
} else {
return binarySearch(arr, target, start, mid - 1);
}
return -1;
}
var arr = [2,4,5,7,8,9,13,23,34,45]
binarySearch(arr, 34) // 8二叉搜索树
构建二叉树及常见方法
最上面的节点成为根节点。每个节点最多有两个子节点。没有子节点的叫做叶子节点。
如图:1所在位置是根节点,2所在位置是1的子节点,是4的父节点。4所在位置是叶子节点。

第一个数作为根节点。
接下来的数如果小于根节点的数值,则放在左边;如果大于根节点的数值,则放在右边。
依次反复,形成二叉树。
定义节点:
function Node(data, left, right) {
this.data = data;
this.left = left;
this.right = right;
}定义节点原型
Node.prototype = {
root: null, // 根节点(属性值)
insert: insert, // 插入节点(方法)
find: find, // 找到某个值对应的节点(方法)
getMix: getMix, // 找到二叉树中的最小值(方法)
getMax: getMax // 找到二叉树中的最大值(方法)
}定义原型方法:将任意节点插入二叉树
// 将任意节点插入二叉树
function insert(data) {
var node = new Node(data, null, null);
if (this.root == null) {
this.root = node;
} else {
var current = this.root;
while(true) {
if (data < current.data) {
if (!current.left) {
current.left = node;
break;
} else {
current = current.left;
}
} else if (data === current.data) {
current = node;
} else {
if (!current.right) {
current.right = node;
break;
} else {
current = current.right;
}
}
}
}
}定义原型方法:根据数值,找到对应节点
function find(data) {
var current = this.root;
while(current != null) {
if (data === current.data) {
return current;
} else if (data < current.data) {
current = current.left;
} else {
current = current.right;
}
}
return null;
}定义原型方法:查找二叉树中的最小值
function getMix() {
var current = this.root;
while(current.left !== null) {
current = current.left
}
return current.data;
}定义原型方法: 查找二叉树中的最大值
function getMax() {
var current = this.root;
while(current.right !== null) {
current = current.right;
}
return current.data;
}二叉树遍历

(1)前序遍历
从二叉树的根结点出发,按照先向左在向右的方向访问,当第一次到达结点时就输出结点数据。
从根结点出发,则第一次到达结点A,故输出A;
继续向左访问,第一次访问结点B,故输出B;
按照同样规则,输出D,输出H;
当到达叶子结点H,返回到D,此时已经是第二次到达D,故不在输出D,进而向D右子树访问,D右子树不为空,则访问至I,第一次到达I,则输出I;
I为叶子结点,则返回到D,D左右子树已经访问完毕,则返回到B,进而到B右子树,第一次到达E,故输出E;
向E左子树,故输出J;
按照同样的访问规则,继续输出C、F、G;
上图前序遍历 输出为ABDHIEJCFG继续向左访问,第一次访问结点B,故输出B;
按照同样规则,输出D,输出H;
当到达叶子结点H,返回到D,此时已经是第二次到达D,故不在输出D,进而向D右子树访问,D右子树不为空,则访问至I,第一次到达I,则输出I;
I为叶子结点,则返回到D,D左右子树已经访问完毕,则返回到B,进而到B右子树,第一次到达E,故输出E;
向E左子树,故输出J;
按照同样的访问规则,继续输出C、F、G;
function frontOrder(node) {
if (node != null) {
console.log(node.data);
frontOrder(node.left);
frontOrder(node.right);
}
}(2)中序遍历
从二叉树的根结点出发,按照先向左在向右的方向访问,当第二次到达结点时就输出结点数据。
从根结点出发,则第一次到达结点A,不输出A,继续向左访问,第一次访问结点B,不输出B;继续到达D,H;
到达H,H左子树为空,则返回到H,此时第二次访问H,故输出H;
H右子树为空,则返回至D,此时第二次到达D,故输出D;
由D返回至B,第二次到达B,故输出B;
按照同样规则继续访问,输出J、E、A、F、C、G;
到达H,H左子树为空,则返回到H,此时第二次访问H,故输出H;
H右子树为空,则返回至D,此时第二次到达D,故输出D;
由D返回至B,第二次到达B,故输出B;
按照同样规则继续访问,输出J、E、A、F、C、G;
function centerOrder(node) {
if (node != null) {
centerOrder(node.left);
console.log(node.data);
centerOrder(node.right);
}
}(3)后序遍历
从二叉树的根结点出发,按照先向左在向右的方向访问,当第三次到达结点时就输出结点数据。
从根结点出发,则第一次到达结点A,不输出A,继续向左访问,第一次访问结点B,不输出B;继续到达D,H;
到达H,H左子树为空,则返回到H,此时第二次访问H,不输出H;
H右子树为空,则返回至H,此时第三次到达H,故输出H;
由H返回至D,第二次到达D,不输出D;
继续访问至I,I左右子树均为空,故第三次访问I时,输出I;
返回至D,此时第三次到达D,故输出D;
按照同样规则继续访问,输出J、E、B、F、G、C,A;
到达H,H左子树为空,则返回到H,此时第二次访问H,不输出H;
H右子树为空,则返回至H,此时第三次到达H,故输出H;
由H返回至D,第二次到达D,不输出D;
继续访问至I,I左右子树均为空,故第三次访问I时,输出I;
返回至D,此时第三次到达D,故输出D;
按照同样规则继续访问,输出J、E、B、F、G、C,A;
function endOrder(node) {
if (node !== null) {
endOrder(node.left);
endOrder(node.right);
console.log(node.data);
}
}二叉树的重建(未完待续)