介绍
二叉搜索树(英语:Binary Search Tree),也称为 二叉查找树、有序二叉树(Ordered Binary Tree)或排序二叉树(Sorted Binary Tree),是指一棵空树或者具有下列性质的二叉树:
- 若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
- 若任意节点的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
- 任意节点的左、右子树也分别为二叉查找树;
- 没有键值相等的节点。
二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低。为O(logn)。二叉查找树是基础性数据结构,用于构建更为抽象的数据结构,如集合、多重集、关联数组等。
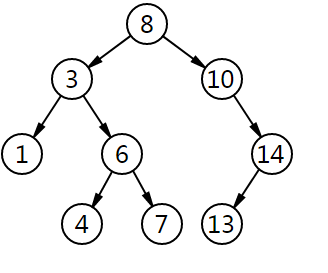
二叉查找树的查找过程和次优二叉树类似,通常采取二叉链表作为二叉查找树的存储结构。中序遍历二叉查找树可得到一个关键字的有序序列,一个无序序列可以通过构造一棵二叉查找树变成一个有序序列,构造树的过程即为对无序序列进行查找的过程。每次插入的新的结点都是二叉查找树上新的叶子结点,在进行插入操作时,不必移动其它结点,只需改动某个结点的指针,由空变为非空即可。搜索、插入、删除的复杂度等于树高,期望O(logn),最坏 O(n)(数列有序,树退化成线性表)。
定义
对于二叉树,我们还是习惯的选择采用链式存储结构实现。它最大的特点,就是他的元素是可以比较大小的。这一点是需要注意的地方
public class BST<E extends Comparable<E>> { //节点可排序比较
private Node root; //根节点
private int size;
public BST(){
root = null;
size = 0;
}
public int size(){
return size;
}
public boolean isEmpty(){
return size == 0;
}
private class Node {
public E e; //节点元素
public Node left; //左子树
public Node right; //右子树
public Node(E e) {
this.e = e;
left = null;
right = null;
}
}
}
插入节点
有了根节点,我们就可以根据二叉树的性质,从根节点出发,构建出一颗二叉树。
// 向二分搜索树中添加新的元素e
public void add(E e){
root = add(root, e);
}
// 向以node为根的二分搜索树中插入元素e,递归算法
// 返回插入新节点后二分搜索树的根
private Node add(Node node, E e){
if(node == null) {
size ++;
return new Node(e);
}
if (e.compareTo(node.e) < 0) { //插入元素如果小于父节点
node.left = add(node.left, e); //父节点左指针 关联上
} else if(e.compareTo(node.e) > 0){ //插入元素如果大于父节点
node.right = add(node.right, e); //父节点右指针 关联上
}
return node;
}
总的来说,就是每次插入一个结点,从根节点出发作比较,小的就往左子树插,大的就往右子树插 一直到叶子节点结束。这和二叉搜索树的定义时完全一致的。
查找元素
查询就比较简单了,就是循环所有节点,看看是否有相同的值,如果有就返回true,否则false
// 在二分搜索树中查找是否包含元素e
public boolean contains(E e) {
return contains(root, e);
}
// 看以node为根的二分搜索树中是否包含元素e, 递归算法
private boolean contains(Node node, E e){
if (node == null) { //找到最低层 没找到返回false
return false;
}
if (e.compareTo(node.e) == 0) { //递归下去的中途找到了返回true
return true;
} else if (e.compareTo(node.e) < 0) { //递归左子树
return contains(node.left, e);
} else {
return contains(node.right, e); //递归右子树
}
}
遍历
/////////////////
// 5 //
// / \ //
// 3 6 //
// / \ \ //
// 2 4 8 //
/////////////////
前序遍历
前序遍历(Preorder Traversal):先访问当前节点,再依次递归访问左右子树
// 二分搜索树的前序遍历
public void preOrder(){
preOrder(root);
}
// 前序遍历以node为根的二分搜索树, 递归算法
private void preOrder(Node node){
if(node == null)
return;
System.out.println(node.e); //先遍历当前节点
preOrder(node.left);
preOrder(node.right);
}
//上图结果:5 3 2 4 6 8
中序遍历
中序遍历(Inorder Traversal):先递归访问左子树,再访问自身,再递归访问右子树
// 二分搜索树的中序遍历
public void inOrder(){
inOrder(root);
}
// 中序遍历以node为根的二分搜索树, 递归算法 中序遍历的顺序就是排序结果
private void inOrder(Node node){
if(node == null)
return;
inOrder(node.left);
System.out.println(node.e); //当前节点输出在中间
inOrder(node.right);
}
//上图结果:2 3 4 5 6 8
二叉搜索树的中序遍历即是一个节点元素升序的结果,相反反向的中序遍历是一个降序的结果
后序遍历
后序遍历(Postorder Traversal):先递归访问左右子树,最后再访问当前节点。
// 二分搜索树的后序遍历
public void postOrder(){
postOrder(root);
}
// 后序遍历以node为根的二分搜索树, 递归算法
private void postOrder(Node node){
if(node == null)
return;
postOrder(node.left);
postOrder(node.right);
System.out.println(node.e);
}
//上图结果:2 4 3 8 6 5
层序遍历(广度优先遍历)
先遍历根节点这一层,再遍历第二层,依次这样从上到下,从左到右。此处实现的思想:利用队列的先入先出的特性
// 层序遍历 也称为广度优先遍历(用队列)
public void levelOrder() {
if (root == null) {
return;
}
Queue<Node> queue = new LinkedList<>();
queue.add(root);
while(!queue.isEmpty()) {
Node node = queue.remove();
System.out.println(node.e);
if (node.left != null) {
queue.add(node.left);
}
if (node.right != null) {
queue.add(node.right);
}
}
}
//上图结果:5 3 6 2 4 8
查询最大、最小值
在二叉树中,最小值肯定在最左侧,最大值肯定在最右侧。所以查询最小最大值,只要循环树左右侧的节点,直到节点没了。
// 寻找二分搜索树的最小元素
public E minimum(){
if(size == 0)
throw new IllegalArgumentException("BST is empty!");
return minimum(root).e;
}
// 返回以node为根的二分搜索树的最小值所在的节点 左子树找到底就是最小值
private Node minimum(Node node){
if(node.left == null)
return node;
return minimum(node.left);
}
// 寻找二分搜索树的最大元素
public E maximum(){
if(size == 0)
throw new IllegalArgumentException("BST is empty");
return maximum(root).e;
}
// 返回以node为根的二分搜索树的最大值所在的节点 右子树找到底 就是最大值
private Node maximum(Node node){
if(node.right == null)
return node;
return maximum(node.right);
}
删除最大、最小值
// 从二分搜索树中删除最小值所在节点, 返回最小值
public E removeMin(){
E ret = minimum();
root = removeMin(root);
return ret;
}
// 删除掉以node为根的二分搜索树中的最小节点
// 返回删除节点后新的二分搜索树的根
private Node removeMin(Node node){
if(node.left == null){ //此时node为最小节点
//把node的右子树挂在node的父亲节点的左子树上
Node rightNode = node.right;
node.right = null;
size --;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
// 从二分搜索树中删除最大值所在节点
public E removeMax(){
E ret = maximum();
root = removeMax(root);
return ret;
}
// 删除掉以node为根的二分搜索树中的最大节点
// 返回删除节点后新的二分搜索树的根
private Node removeMax(Node node){
if(node.right == null){ //此时node为最大节点
//把node的左子树挂在node的父亲节点的右子树上
Node leftNode = node.left;
node.left = null;
size --;
return leftNode;
}
node.right = removeMax(node.right);
return node;
}
删除指定元素的节点
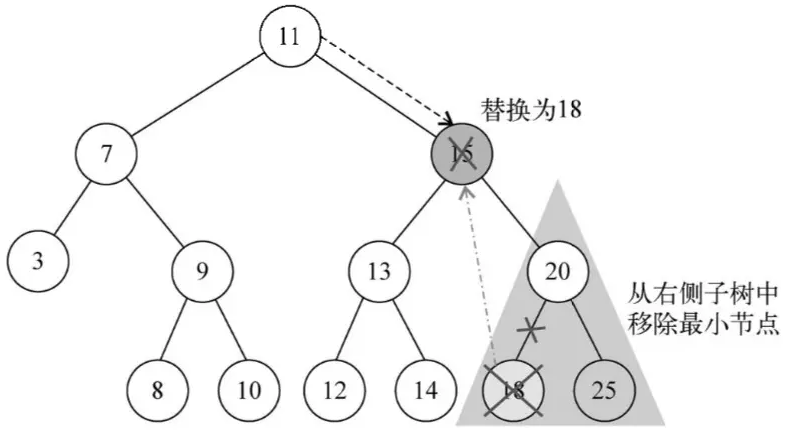
删除节点稍微比较复杂。 其中最重要的是移除含有2个子节点的节点比较复杂,如图所示,如果要删除15这个元素,需要在他的右子树寻找最小的节点18,用这个最小的节点替换15。(或者在15的左子树找最大的元素14来替换15)。这样才能满足二叉搜索树的条件。
要被删除节点的右子树的最小值都大于它左子树的值,且都小于它右子树的值。
// 从二分搜索树中删除元素为e的节点
public void remove(E e){
root = remove(root, e);
}
// 删除掉以node为根的二分搜索树中值为e的节点, 递归算法
// 返回删除节点后新的二分搜索树的根
private Node remove(Node node, E e){
if( node == null )
return null;
if( e.compareTo(node.e) < 0 ){
node.left = remove(node.left , e);
return node;
}
else if(e.compareTo(node.e) > 0 ){
node.right = remove(node.right, e);
return node;
}
else{ // e.compareTo(node.e) == 0
// 待删除节点左子树为空的情况
if(node.left == null){
Node rightNode = node.right;
node.right = null;
size --;
return rightNode;
}
// 待删除节点右子树为空的情况
if(node.right == null){
Node leftNode = node.left;
node.left = null;
size --;
return leftNode;
}
// 待删除节点左右子树均不为空的情况
// 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
// 用这个节点顶替待删除节点的位置
Node successor = minimum(node.right);
successor.right = removeMin(node.right);
successor.left = node.left;
node.left = null;
node.right = null;
return successor;
}
}
总结
二叉搜索树虽然简单但在最坏情况下表现得并不好(退化为链表),最坏效率是 O(n)。不过它是其他树类型的数据结构的基础,支持动态查询,且有很多改进版的二叉查找树可以使树高为 O(logn),从而将最坏效率降至 O(logn),如 AVL树、红黑树等。完整代码移步到Github