强连通
在有向图中,如果v-w存在一条路径,w-v也存在一条路径,那么称v和w是强连通的。
strong components
在有向图中,存在一个最大的子集,其中每一个节点都与其他节点是强连通的,这样的子集叫做 strong connected components,简称strong components。
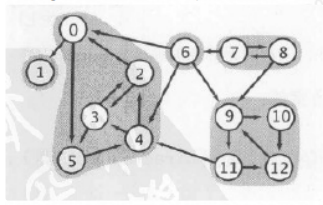
例如,这张图中: strong components有:
1
0,2,3,4,5
6
7,8
9,10,11,12
环在这里有很大影响:
一个强连通图有一个strong component。
一个节点为V的有向无环图有V个strong components。
kosaraju算法
1.先将图反转,计算反转图的逆后序排列
2.按照1中的排列对图进行深度优先搜索
3.在同一个递归中的深度优先搜索的节点在一个strong component中
类:
DirectGraph:有向图
DFSOrder:计算逆后序排列
Kosaraju:Kosaraju算法
具体代码见git。
Kosaraju算法过程
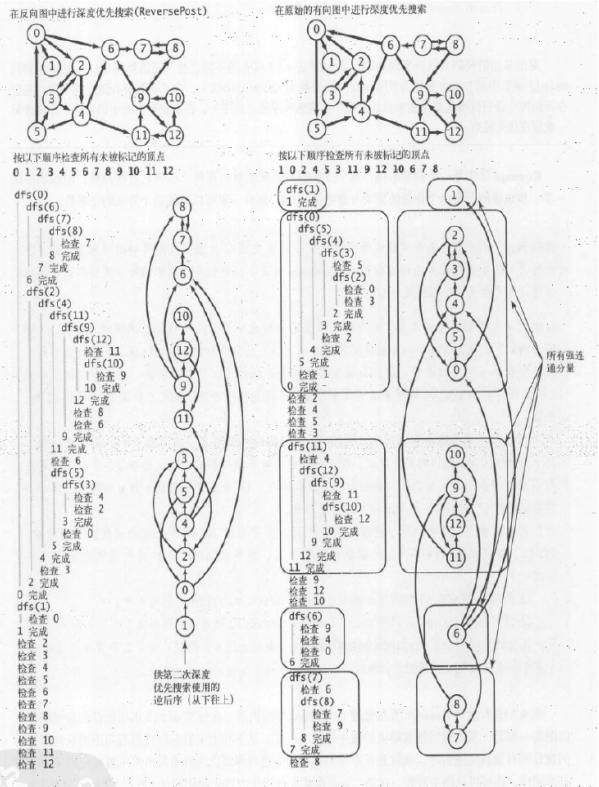
Kosaraju算法推导
1.首先证明:如果v与s强连通,那么v一定在s的dfs递归中。
假设节点v不在s的dfs递归中,那么v一定是在以前就被dfs处理过了,但是由于v-s,那么s会在v存在的递归中也被处理过了,那么s不会被构造函数调用。
得证。
2.其次证明:对s进行dfs到达的节点v,一定与s强连通。
整理条件:G中s-v,在GR(G的反向图,下图)中v在s的后面
》》:GR中v-s,在GR中v在s的后面
》》:GR中v-s,在GR中v的dfs比s的dfs先结束。
》》:GR中v-s,
a.dfs(v)比dfs(s)先调用,先结束。
b.或者dfs(v)比dfs(s)晚调用,先结束。
》》:GR中v-s,
a.不可能,因为存在v-s,那么dfs(v)不会比dfs(s)先结束
b.可能,此时s-v
》》:GR中v-s,s-v
》》:G中s-v,v-s
得证。
我的理解发散: MyCustomKosaraju算法
由Kosaraju算法推导可知,只是要制造一种情况,就是v-s,且dfs(v)比dfs(s)先结束。那么相对于原先的GR中的v-s,dfs(v)比dfs(s)先结束,我们只要在G中s-v,且dfs(s)比dfs(v)先结束就好了。
由于dfs的结束顺序是由DFSOrder计算出的逆后序排列,也就是在这个排列中,靠右的比靠左的先结束。我们可以很简单的把G的后逆序排列反转,那么靠左的dfs比靠右的dfs先结束了。
kosaraju算法
1.先将图反转,计算反转图的逆后序排列
2.按照1中的排列对图进行深度优先搜索
3.在同一个递归中的深度优先搜索的节点在一个strong component中
MyCustomKosaraju算法
1.计算图的逆后序排列,反转逆后续排列
2.按照1中的排列对图进行深度优先搜索
3.在同一个递归中的深度优先搜索的节点在一个strong component中
两者区别在于,反转图的逆后序排列 vs 图的逆后序排列的反转
MyCustomKosaraju优势:
1.节省空间
2.理解方便
类:
MyCustomKosaraju
具体代码见git。
MyCustomKosaraju算法推导
1.首先证明:如果v与s强连通,那么v一定在s的dfs递归中。
假设节点v不在s的dfs递归中,那么v一定是在以前就被dfs处理过了,但是由于v-s,那么s会在v存在的递归中也被处理过了,那么s不会被构造函数调用。
得证。
2.其次证明:对s进行dfs到达的节点v,一定与s强连通。
整理条件:G中s-v,在GR(G的反向图,下图)中v在s的后面
》》:GR中v-s,在GR中v在s的后面
》》:GR中v-s,在GR中v的dfs比s的dfs先结束。
》》:GR中v-s,
a.dfs(v)比dfs(s)先调用,先结束。
b.或者dfs(v)比dfs(s)晚调用,先结束。
》》:GR中v-s,
a.不可能,因为存在v-s,那么dfs(v)不会比dfs(s)先结束
b.可能,此时s-v
》》:GR中v-s,s-v
》》:G中s-v,v-s
得证。
整理条件:G中s-v,在G的后逆序排列的反转中v在s的后面
》》:G中s-v,dfs(s)比dfs(v)先结束
》》:G中s-v,
a.dfs(s)比dfs(v)先调用,先结束。
b.dfs(s)比dfs(v)晚调用,先结束。
》》:G中s-v,
a.不可能,因为存在s-v,那么dfs(s)不会比dfs(v)先结束
b.可能,此时v-s
》》:G中s-v,v-s
得证。
结果演示
