题目链接 leetcode-cn.com/problems/fa… 历时一个月想出的题解,自认为是最佳题解了,仅仅用单链表就解决了题目。 文字部分会比较啰嗦,也可以直接看代码。
首先看题目。 题目的大概意思就是,从0开始的数轴上会源源不断的掉下方块,这些方块会叠起来。然后问的是每次掉下方块后的最高高度。
在leetcode做题很有意思的是题目的提示。 1 <= 方块个数 <= 1000. 1 <= 方块左下角的x坐标 <= 10^8. 1 <= 方块的宽高 <= 10^6. 那么初步的印象,这方块掉落大概是这样子的,后面掉落的方块叠在前面掉落的方块上。
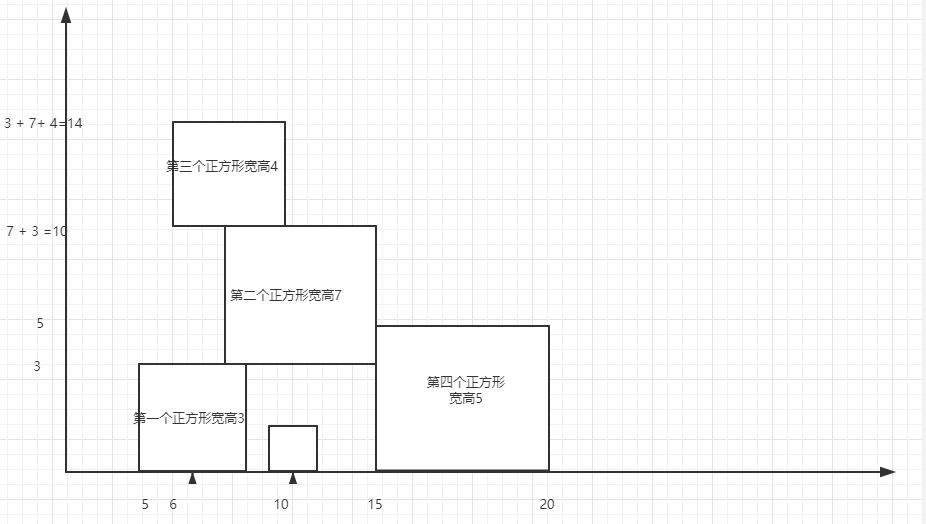
(图画的差一点将就看看)
那么问题来了,图里是一个二维坐标系,难道是用二维数组去解决吗? 但是这不可能的,因为方块的宽高上限都很高,任何一道算法题都不可能给这么大的空间(10^8 * 10^6的二维数组) 而且这道题问的只是最高高度,所以只用一个一维数组就可以了,这数组装当前状态下,每两个坐标之间的当前高度。 比如上图 [5, 6]的高度为第一个正方形的高度 [6, 10]的高度为第一个正方形 + 第二个正方形 + 第三个正方形的高度 [10, 15]的高度为第一个正方形 + 第二个正方形 最后[10, 15]就是最后一个正方形自己的高度,而那个没有名字的正方形……不重要
所以变成数组大概就是 [0, 0, 0, 0, 0, 3, 14, 14, 14, 14, 10, 10, 10, 10, 10, 10, 5, 5, 5, 5, 5]
所以我们要做的事情大概就是,每落下一个方块,遍历方块(position[0], position[0] + position[1])这区间,取最高的高度,加上现在这方块的高度,更新这区间的高度,然后更新最高高度即可。
然而还是不行,正方形的左下方x坐标最大值是10^8, 而算法题不会给到10^8这么大的空间 假如第一个掉下来的是在10^8次方的位置掉了一个宽高为1的正方形,那么数组就会是[0, ..., 0, 1] 这样子,前面的那好多好多个0,其实可以用更好的方法去表达。
那就是链表 Class Link(){ next, // 下一个节点 start, // 这一段开始的下标 end, // 这一段结束的下标 height // 这一段的高度 } 这样前面的那些0,就可以变成start = 1, end = 10 ^ 8 - 1, height = 1的一个节点,省下了好多空间
如果这时候开始写代码,会发现操蛋的很…… 链表虽然能省空间,但是却不省事……
比如上面第二个正方形砸下去的时候,要把第一个正方形切成两部分,一部分被盖住了,更新高度;另一部分露了出来,高度不变。 然后第三个正方形来了,他砸了下来,又盖住了第一个正方形的一部分,并且盖住第二个正方形的一部分
真的写起来会发现节点的拆分/添加/减少(一个很大的正方形砸下来,可能之间把几个节点之间合成一个) 麻烦死了!
为了处理方便,每次落下我都把链表分成三部分[head, front], (front, back), [back, tail] 我遍历链表,找到front,也就是在落下正方形左边的第一个节点 back,落下正方形右边的第一个节点,且这两个节点都跟落下的正方形没有瓜葛,也就是不会被落下的正方形盖住
然后以front为前驱节点, back为后驱节点,只是替换(front, back)这一段,这样我只要看看front.next是否有露出一部分, back的前一个节点是否有露出一部分,然后加上落下的正方形,这样我最多只需要操作三个节点,简化了代码
下面是自认为通俗易懂的代码 /* 核心思路是: 因为这题只考虑高度,所以我们只要考虑每段坐标上的高度就可以了,但是因为数值比较大 直接用数组的话会空间不够,所以用链表 每次落下方块时,把链表分成三部分[head, front], (front, back), [back, tail] front以及front之前的节点,是不会收到本次落下的影响的 同理,back以及back之后的节点,也不会受到本次落下的影响
这道题棘手的地方在于很难处理落下后产生的影响,因为可能这次落下的方块覆盖了很多个节点, 也可能只是创建一个新的节点,还可能把一个已有的节点分成两部分 为了处理起来能简单一些,每次落下的时候,不管情况如何,直接替换(front, back)这一段 为了情况能统一处理,因此加了head和tail,确保每一次落下都能找到front和back */
function Link(start, end, height, next){
this.next = next; // 下一段的节点
this.start = start; // 这一段的开始坐标
this.end = end; // 这一段的结束坐标
this.height = height; // 这一段的高度
}
var fallingSquares = function(positions) {
let head = null;
let tail = null;
let res = [];
let maxHeight = 0;
tail = new Link(Number.MAX_VALUE, Number.MAX_VALUE, 0, null);
head = new Link(-1, -1, 0, tail);
for (let i = 0; i < positions.length; ++i){
let start = positions[i][0];
let end = start + positions[i][1];
let height = positions[i][1];
let front = head;
let back = head;
let tmp = head;
// 找front和back
while (tmp){
if (tmp.end <= start)
front = tmp;
if (end <= tmp.start){
back = tmp;
break;
}
tmp = tmp.next;
}
// 保存back的前一个,不然后面修改链表的时候会丢失
let backfront = head;
while (backfront.next !== back){
backfront = backfront.next;
}
// 找到(front, back)中最高的高度,这次的方块会叠在这高度之上
let newHeight = 0;
// 从这里开始遍历高度
tmp = front.next;
while (tmp !== back){
if (tmp.height > newHeight)
newHeight = tmp.height;
tmp = tmp.next;
}
// 看看front.next是否被分成两段, front.next.start 到 start这一段还是原来的高度,但是start之后就会被刷新高度
if (front.next && front.next.start < start){
let link = new Link(front.next.start, start, front.next.height, null);
front.next = link;
front = front.next;
}
// 本次落下的方块加入链表
let link = new Link(start, end, height + newHeight, back);
if (link.height > maxHeight)
maxHeight = link.height;
front.next = link;
front = front.next;
// 把back前一个看看,end 到 backfront.end之间还是原来的高度
if (end < backfront.end){
let link = new Link(end, backfront.end, backfront.height, back);
front.next = link;
}
res.push(maxHeight);
// print(head);
}
return res;
};