最近在学习算法,决定读完的书,都用脑图记录一下。方便回顾知识。
介绍
本书以 iOS 和 Android 平台上的应用程序“算法动画图解”为基础,以图配文,详细讲解 了各种算法和数据结构的基本原理。是一本不错的入门书籍。
前言
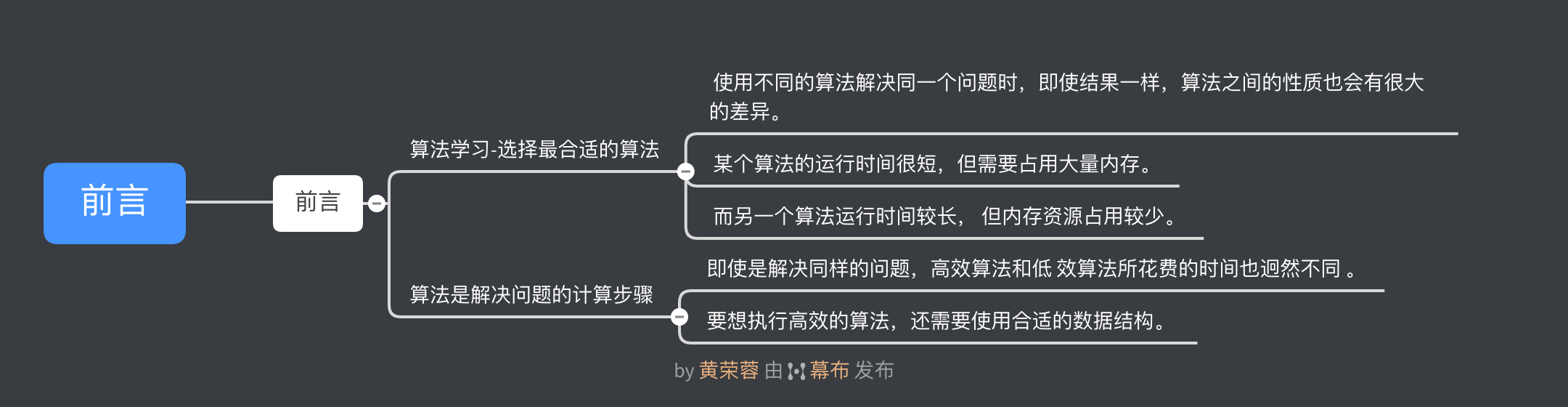
算法和程序有些相似,区别在于程序是以计算机能够理解的编程语言编写而成的,可以在 计算机上运行,而算法是以人类能够理解的方式描述的,用于编写程序之前。不过,在这个过 程中到哪里为止是算法、从哪里开始是程序,并没有明确的界限。
序章
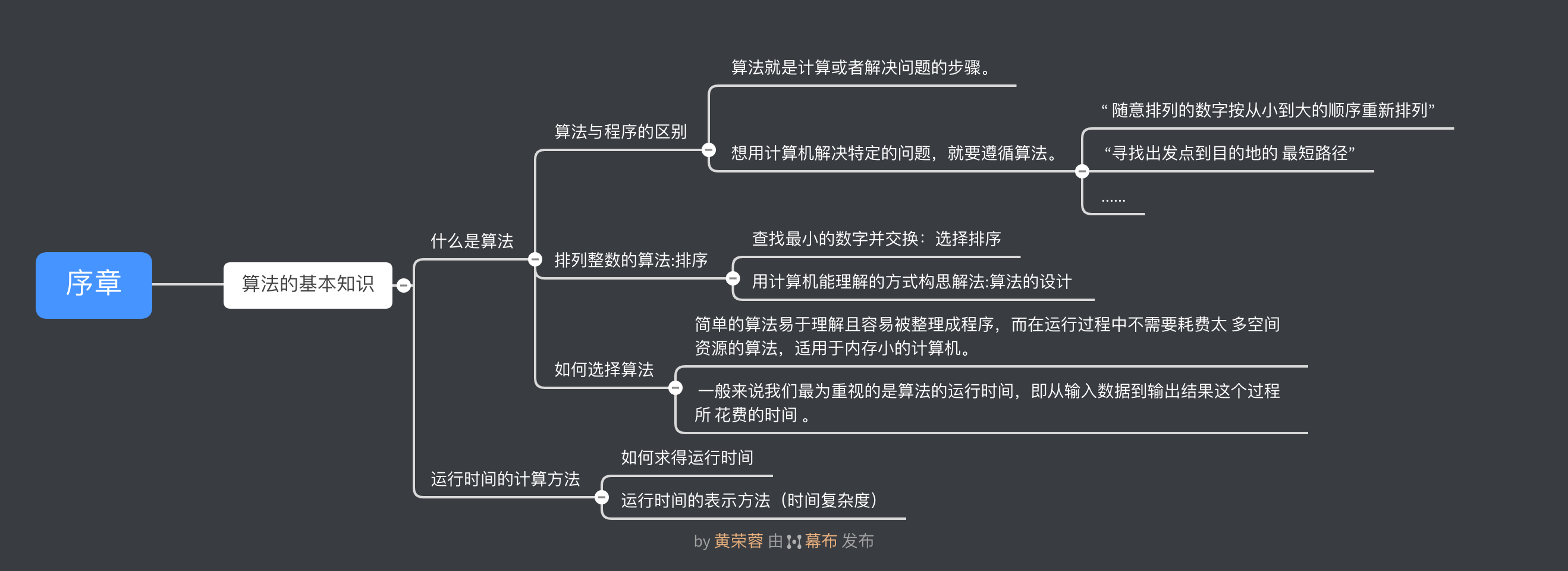
排列问题算法示例
这是一个以随意 排列的整数为输入,把它们按从小到大的顺序重新排 列的问题。虽然在这个示例中输入的整数个数 n 为 8, 然而不管 n 多大,算法都必须将问题解决。
思路(选择排序):先从输入的数字中找出最小的数字,再将它和最左边的数字交换位置。在这个示例中就是找到最小数字 1,然后将它和最左边的 7 交换位置。
1 的位置固定下来后不再移动。接下来,在剩下的数字里继续寻找最小数,再将它和左边第 2 个数字交换位置。于是,4 和 13 也交换了位置。
我们将这样的一次交换称为“1 轮”。到了第 k 轮的时候,就把剩下的数字中最小的一个, 与左边开始第 k 个数字进行交换。于是在结束第 k 轮后,从左数的 k 个数字便都按从小到大的 顺序排列了。只要将这个步骤重复 n 次,那么所有的数字都将按从小到大的顺序排列。

算法的设计
计算机擅长高速执行一些基本命令,但无法执行复杂的命令。此处的“基本命令”指的是 “做加法”或者“在指定的内存地址上保存数据”等。
计算机是以这些基本命令的组合为基础运行的,面对复杂的操作,也是通过搭配组合这些基本命令来应对的。
如何选择算法
① 生成一个由 n 个数字构成的数列(不和前面生成的数列重复)
②如果1中生成的数列按从小到大的顺序排列就将其输出,否则回到步骤①
解决思路一:“全排列算法” (低效率算法)
全排列算法列出了所有的排列方法,所以不管输入如何,都可以得到正确的结果。
需要多久能出结果?若运气好,很快就能出现正确排列。
然而,最差情况是直到最后才出现正确排列,计算机就得确认所有可能的排列。
n 个数字有 n! 种不同的排列方法(n! = n(n - 1)(n - 2)...3·2·1)。
现在,我们来看看 n = 50时的运行情况。
① 50! = 50·49·48...3·2·1
② 50·49·48...3·2·1 > 50·49·48...13·12·11
③ 50·49·48...13·12·11 > 10^40
公式①中,50! 即为数字1到数字50的乘积。为了便于计算,通过公式②③将结果近似转换为10的n次方的形式。
公式②右边部分去掉了10以下的数字,因此小于50!。公式③左右都是40个数字的乘积,且左边数字都大于10,
因此大于右边的10^40。接下来我们就用10^40近似代表50个数字的所有排列情况来进行计算。
假设1台高性能计算机1秒能检查 1万亿(= 10^12)个数列,那么检查 10^40个数列将花费的时间为
10^40÷10^12 = 10^28 秒。1年为31536000秒不到10^8秒。因此,10^28秒>10^20年。
从大爆炸开始宇宙已经经历了约 137 亿年,即便如此也少于 10^11 年。
也就是说,仅仅是对50个数字进行排序,若使用全排列算法,就算花费宇宙年龄的 10^9 倍时间也得不出答案。
解决思路二:“选择排列算法”
首先,为了在第 1 轮找到最小的数字,需要从左往右确认数列中的数字,只要查询n个数字即可。
在接下来的第 2 轮中,需要从n-1 个数字中寻找最小值,所以需要查询n-1个数字。
将这个步骤进行到第 n 轮的时候,需要查询的次数如下。
n+(n-1)+(n-2)+...3+2+1= n(n+1)/2 ≤ n^2 / 2
n=50的时候n^2=2500。假设1秒能确认1万亿(=10^12)个数字,那么2500÷10^12=0.000 000 002 5秒便能得出结果。
比全排列算法的效率高得多。
1 数据结构
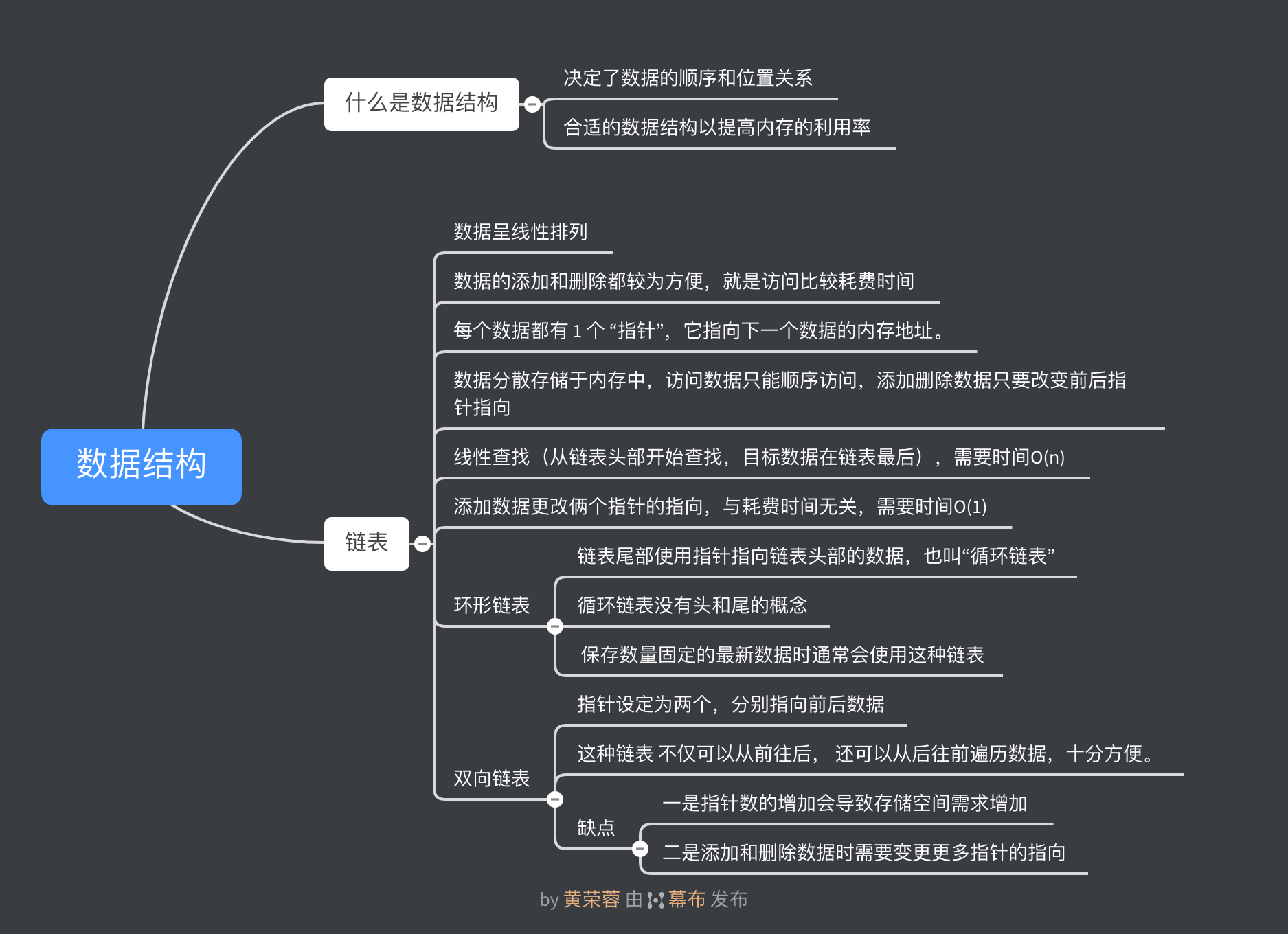
1-1 什么是数据结构
决定了数据的顺序和位置关系
数据存储于计算机的内存中。数据存储于内存时,决定了数据顺序和位置关系便是“数据结构”。
选择合适的数据结构以提高内存的利用率
数据在内存中是呈线性排列的,但是我们 也可以使用指针等道具,构造出类似“树形”的复杂结构(树形结构将在 4-2 节详细说明)。
1-2 链表
数据呈线性排列。在链表中,数据的添加和删除都较为方便,就是访问比较耗费时间。
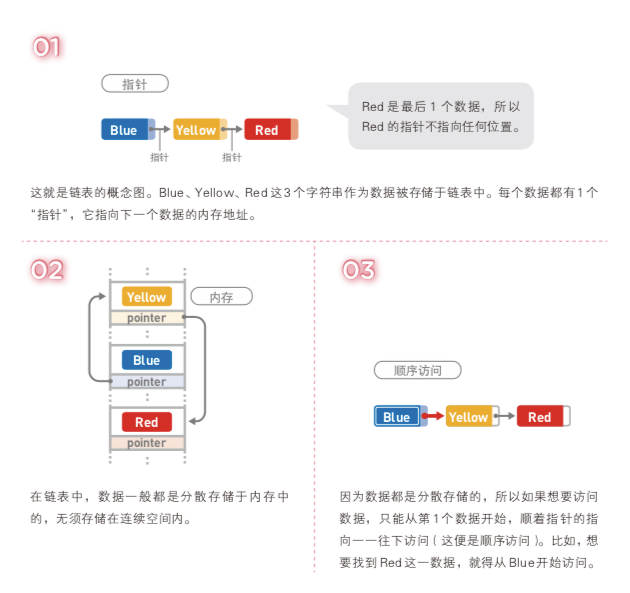
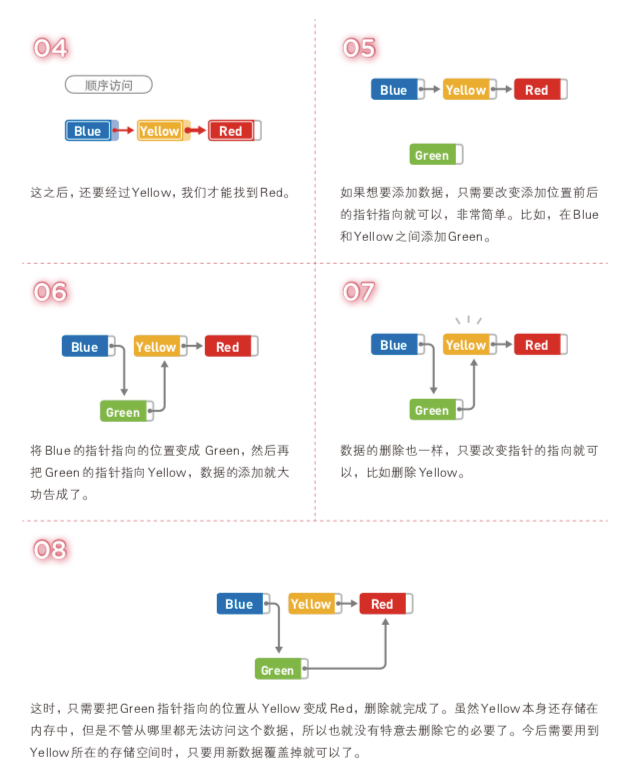
对链表的操作所需的运行时间是多少呢?
把链表中的数据量记成n。访问数据时,从链表头部开始查找(线性查找),如果目标数据在链表最后 的话,需要的时间就是 O(n)。
另外,添加数据只需要更改两个指针的指向,所以耗费的时间与 n 无关。如果已 经到达了添加数据的位置,那么添加操作只需花费 O(1) 的时间。删除数据同样也只需 O(1) 的时间。
