js算法相关

数组去重

• 利用set

function distinct(a){
    return Array.from(new set([...a]));
}

• 利用object的属性没有重复

function distinct(a){
    let result=[];
    let obj={};
    for(let i of a){
        if(!obj[i]){
            result.push(i);
            obj[i]=1;
        }
    }
}

数组排序

• sort() 方法
  接收俩个参数，返回负数则第一个数在前面，返回正数则第一个数在后面，相等就返回0

function mysort(a,b){
    return a-b;
}
arr.srot(mysort)

• 冒泡排序 （俩俩比较，大的数会一直换到最后的位置）
  第一层循环是总共要排序的次数是length-1
  第二层循环是在无序的数据里面选最大的，大的则往后排

function maopao(a){
    for(let i=0;i<a.length-1;i++){
        for(let j=0;j<a.length-1-i;j++){
            if(a[j]>a[j+1]){
                let temp=a[j];
                a[j]=a[j+1];
                a[j+1]=temp;
            }
        }
    }
}

• 快速排序 （运用递归的思想，二分法）
  1.如果数组长度为1的就直接返回该数组（递归的结束条件）
  2.取中间的值的索引，然后取中间值 () 3.定义左右数组，小的放左边，大的放右边
  4.返回左右的值，concat一下左边递归+中间值（因为已经删除了）+右边递归

function quickSort(a){
    if(a.length<=1){
        return a;
    }
    let index=Math.floor(a.length/2);
    let indexVal=a.splice(index,1);
    let left=[];
    let right=[];
    for(let i=0;i<a.length;i++){
        if(a[i]<indexVal){
            left.push(a[i]);
        }else{
            right.push(a[i]);
        }
    }
    return quickSort(left).concat(indexVal,quickSort(right));
}

• 插入排序 （第一个为有序的，让后面的全为无序的部分，无序的部分和有序的部分一个个比较后插入）
  1.循环是从1开始外循环为i（i就是第一个无序的数）
  2.内循环是从有序的部分开始，j=i；j--的，前一个数大于后一个数时候需要调换位置

function insertSort(a){
    let temp;
    for(let i=1;i<a.length;i++){
        for(let j=i;j>0 && a[j]<a[j-1];j--){
            temp=a[j];
            a[j]=a[j-1];
            a[j-1]=temp;
        }
    }
    return a;
}

数组查询

• 二分法查询一个排序好的数组

function binarySerch(arr, key, start, end) {
    if(start>end){
        return false;
    }
    let mid=Math.floor((end-start)/2);
    if(arr[mid]<key){
        return binarySerch(arr,key,mid+1,end);
    }else if(arr[mid]>key){
        return binarySerch(arr,key,start,mid-1);
    }else{
        return mid;
    }
}

二叉树

• 树的基础知识
  度：子节点个数
  满二叉树：全部子节点都是2个
  完全二叉树：非最后一层都是子节点都是2，最后一层的子节点不能只有右侧节点

• 前序遍历：访问根–>遍历左子树–>遍历右子树;（深度遍历）第一个是访问根

• 中序遍历：遍历左子树–>访问根–>遍历右子树;（深度遍历）第一个是访问最左边

• 后序遍历：遍历左子树–>遍历右子树–>访问根;（深度遍历）第一个是访问最左边

• 广度遍历：按照层次一层层遍历;第一个是根

前序遍历：- + a * b c / d e
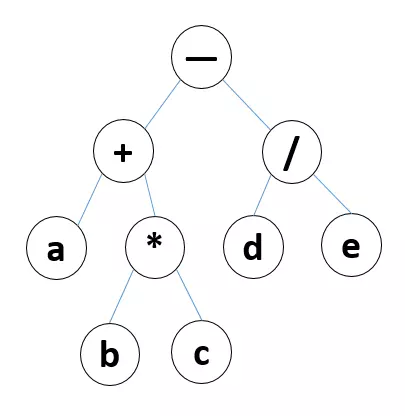
中序遍历：a + b * c - d / e
后序遍历：a b c + d e / -
广度遍历：- + / a * d e b c

• 树的结构

var tree = {
    value: "-",
    left: {
        value: '+',
        left: {
            value: 'a',
        },
        right: {
            value: '*',
            left: {
                value: 'b',
            },
            right: {
                value: 'c',
            }
        }
    },
    right: {
        value: '/',
        left: {
            value: 'd',
        },
        right: {
            value: 'e',
        }
    }
}

• 前序遍历

let result=[];
function dfs(node){
    if(node){
        result.push(node.value);
        dfs(node.left);
        dfs(node.right);
    }
}

• 中序遍历

let result=[];
function dfs(node){
    if(node){
        dfs(node.left);
        result.push(node.value);
        dfs(node.right);
    }
}

• 后序遍历

let result=[];
function dfs(node){
    if(node){
        dfs(node.left);
        dfs(node.right);
        result.push(node.value);
    }
}

• 广度遍历

let result=[];
let stack=[tree];//需要遍历的节点放入数组中，（后续会将其平铺）
let count = 0; // 用来记录执行到第几层
function bfs(){
    let node=stack[0];
    if(node){
        result.push(node.value);
        if(node.left) stack.push(node.left);
        if(node.right) stack.push(node.right);
        count++;
    }
    bfs();
}