搜索
搜索分为广度优先搜索BFS和深度优先搜索DFS。
- BFS一般用来解决路径最短问题,需要存储已经遍历过的节点,防止重复遍历,还需要用队列存储需要遍历的节点
- DFS适合用来解决所有解问题。,DFS需要回溯。
1091. 二进制矩阵中的最短路径(Medium)
在一个 N × N 的方形网格中,每个单元格有两种状态:空(0)或者阻塞(1)。
一条从左上角到右下角、长度为 k 的畅通路径,由满足下述条件的单元格 C_1, C_2, ..., C_k 组成:
相邻单元格 C_i 和 C_{i+1} 在八个方向之一上连通(此时,C_i 和 C_{i+1} 不同且共享边或角)
C_1 位于 (0, 0)(即,值为 grid[0][0])
C_k 位于 (N-1, N-1)(即,值为 grid[N-1][N-1])
如果 C_i 位于 (r, c),则 grid[r][c] 为空(即,grid[r][c] == 0)
返回这条从左上角到右下角的最短畅通路径的长度。如果不存在这样的路径,返回 -1 。
题解:题目要我们求从左上角到右下角的最短距离,可以使用BFS,首先要保证左上角和右下角的值为“0”,然后定义八个方向,用一个队列存储要走的点,当有一个到达右下角的时候就返回,走过的点值变为“1”。
class Solution {
public int shortestPathBinaryMatrix(int[][] grid){
int m = grid.length;
int n = grid[0].length;
//如果左上角和右下角为1,返回-1
if (grid[0][0] == 1 || grid[m - 1][n - 1] == 1){
return -1;
}
//左上角的点可以走,设为1
grid[0][0] = 1;
//设置8个方向
int[][] dir = {{1, 0}, {1, 1}, {1,-1}, {0, 1}, {0, -1}, {-1, 0},{-1, -1}, {-1, 1}};
//准备一个队列保存每一个格子可以走的步
Queue<int[]> queue = new LinkedList<>();
queue.add(new int[]{0, 0});
//准备一个c,用来跟队列长度做比较,知道何时走完队列长度
int len = queue.size();
int c = 0;
int path = 1;
//广度优先搜索
while (!queue.isEmpty()){
int[] data = queue.poll();
//x,y代表当前坐标
int x = data[0];
int y = data[1];
//如果走到最后一步,返回
if (x == m - 1 && y == n - 1){
return path;
}
//填充队列,将可走的步添加进队列
for (int[] d : dir){
// x1,y1代表当前坐标移动后的坐标(x1,y1)
int x1 = x + d[0];
int y1 = y + d[1];
if (x1 >= 0 && y1 >= 0 && x1 < m && y1 < n && grid[x1][y1] == 0){
queue.add(new int[]{x1, y1});
grid[x1][y1] = 1;
}
}
c++;
//走完队列长度,重新赋值c和len,path++
if (c == len){
c = 0;
path++;
len = queue.size();
}
}
return -1;
}
}
279. 完全平方数(Medium)
给定正整数 n,找到若干个完全平方数(比如 1, 4, 9, 16, ...)使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。
示例 1:
输入: n = 12
输出: 3
解释: 12 = 4 + 4 + 4.
示例 2:
输入: n = 13
输出: 2
解释: 13 = 4 + 9.
本题可以使用“四平方和定理”来解答,但是这种解法不具有普遍性,略过。
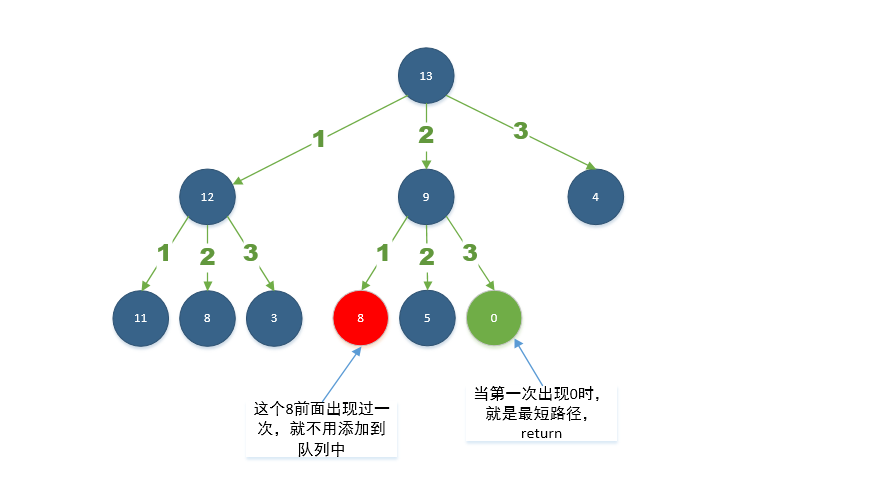
题解:一个正整数n,找到最少n个完全平方数的和等于n,可以想到使用BFS来解答。于是转换成“求n到0的最短距离”,当两个数大小相差一个数的平方时,表示可以达到,借用一张图
class Solution {
public int numSquares(int n) {
//准备一个队列,存储需要遍历的节点
Queue<Pair<Integer, Integer>> queue = new LinkedList<>();
//准备一个数组,用来标记节点是否遍历过
boolean[] record = new boolean[n + 1];
queue.add(new Pair(n, 0));
//开始广度优先遍历
while (!queue.isEmpty()){
int val = queue.peek().getKey();
int step = queue.peek().getValue();
queue.remove();
//每一层的广度优先遍历
for (int i = 1; ; i++) {
int nextVal = val - i * i;
//说明已经达到最大平方数
if (nextVal < 0){
break;
}
//找到了最短路径
if (nextVal == 0){
return step + 1;
}
// 当再次出现时没有必要加入,因为在该节点的路径长度肯定不小于第一次出现的路径长
if (!record[nextVal]){
queue.add(new Pair<>(nextVal, step + 1));
record[nextVal] = true;
}
}
}
return -1;
}
}
127. 单词接龙(Medium)
给定两个单词(beginWord 和 endWord)和一个字典,找到从 beginWord 到 endWord 的最短转换序列的长度。转换需遵循如下规则:
每次转换只能改变一个字母。 转换过程中的中间单词必须是字典中的单词。
说明:
如果不存在这样的转换序列,返回 0。
所有单词具有相同的长度。
所有单词只由小写字母组成。
字典中不存在重复的单词。
你可以假设 beginWord 和 endWord 是非空的,且二者不相同。
示例 1:
输入:
beginWord = "hit",
endWord = "cog",
wordList = ["hot","dot","dog","lot","log","cog"]
输出: 5
解释: 一个最短转换序列是 "hit" -> "hot" -> "dot" -> "dog" -> "cog",返回它的长度 5。
示例 2:
输入:
beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]
输出: 0
解释: endWord "cog" 不在字典中,所以无法进行转换。
题解:由题意可得,我们要将beginWord变为endWord,一次只能变一个字符,且变换后的单词需要在字典里。那么首先需要判断endWord是否在字典里,如果不在直接返回0。
- 最开始想到可以根据startWord与endWord的区别,每次替换一个字符,然后看字典是否存在,但是这个方法容易找不到中间状态;
- 可以每个字符都用‘a’~‘z’来替换,然后判断是否存在于字典,存在的话就添加进队列,然后进行下一轮遍历,这时候就变成了广度优先遍历。
class Solution {
public static int ladderLength(String beginWord, String endWord, List<String> wordList) {
//如果wordList不包含endWord,直接返回0
if (!wordList.contains(endWord)){
return 0;
}
//将wordList里的元素存储进set
HashSet<String> set = new HashSet<>(wordList);
//准备一个queue
Queue<String> queue = new LinkedList<>();
queue.add(beginWord);
int res = 1;
while (!queue.isEmpty()){
//BFS
for (int i = 0; i < queue.size(); i++) {
String word = queue.poll();
if (word.equals(endWord)){
return res + 1;
}
for (int j = 0; j < word.length(); j++) {
//将单词的每个字符都从'a'-'z'替换一遍
String newWord = word;
for (char ch = 'a'; ch <= 'z'; ch++) {
newWord = replaceChar(newWord, j, ch);
//如果newWord没有遍历过且不等于word
if (set.contains(newWord) && !newWord.equals(word)) {
queue.add(newWord.toString());
set.remove(newWord.toString());
}
}
}
}
++res;
}
return 0;
}
//替换字符串指定位置的字符
private static String replaceChar(String str, int index, char ch){
char[] chars = str.toCharArray();
chars[index] = ch;
return String.valueOf(chars);
}
}