Given n non-negative integers a1, a2, ..., an , where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.
Note: You may not slant the container and n is at least 2.
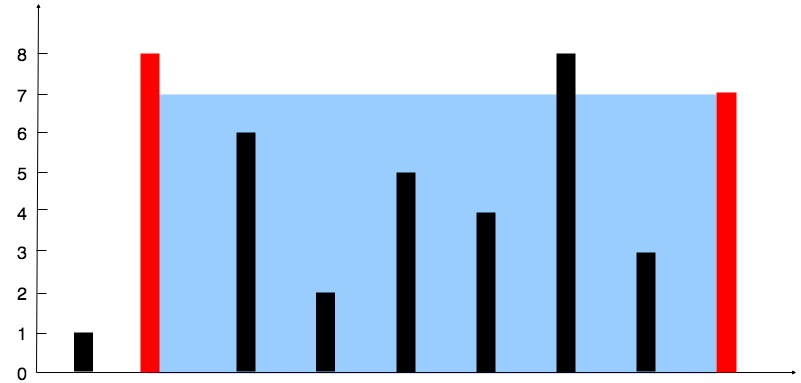
The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.
Example:
Input: [1,8,6,2,5,4,8,3,7]
Output: 49
首先想到的是暴力解决方案:
class Solution {
public:
int maxArea(vector<int>& height) {
int max_area = 0;
for (int begin = 0; begin < height.size() - 1; begin ++) {
for (int end = begin + 1; end < height.size(); end ++) { int length = end - begin;
int area = length * min(height[begin], height[end]);
max_area = max(max_area, area);
}
}
return max_area;
}
};
但是超时了
同时还想到了两个指针的做法,但是没有想的特别明白。所以后来是看了solution之后才确认这种方法可以做。
class Solution {
public:
int maxArea(vector<int>& height) {
int max_area = 0;
int begin = 0;
int end = height.size() -1;
while (begin < end) {
int area = (end - begin) * min(height[begin], height[end]);
max_area = max(max_area, area);
if (height[begin] < height[end]) {
begin ++;
}
else {
end --;
}
}
return max_area;
}
};
这是官方的解释,使用两个指针来做。因为这个容器最终取决于短一点"挡板"的高度,所以,每次都移动指向的"挡板"较低的指针,以期寻找到更高的挡板,从而使容器能容纳更多的水。
The intuition behind this approach is that the area formed between the lines will always be limited by the height of the shorter line. Further, the farther the lines, the more will be the area obtained.
We take two pointers, one at the beginning and one at the end of the array constituting the length of the lines. Futher, we maintain a variable \text{maxarea}maxarea to store the maximum area obtained till now. At every step, we find out the area formed between them, update \text{maxarea}maxarea and move the pointer pointing to the shorter line towards the other end by one step.