从斐波那契数列中解析优化递归与循环
每当我们谈到递归和循环的例子,斐波那契数列总会被第一个提出来,其次可能也是斐波那契数列的变种,所以斐波那契数列是一个非常经典的例子。
首先我们知道斐波那契数列其实就是前两项为1,从第三项开始每一项都为都为前两项之和,所以我们根据常规的递归方式来写出解决方法:
常规解法
function Fibonacci (n) {
return n < 2 ? n : Fibonacci(n-1) + Fibonacci(n-2);
}
此时我们写出的代码简洁美观,但同时也暴露出很大的弊端:函数调用自身,存在很大的性能损耗。每一次函数调用都要在内存栈中分配空间保存参数、返回地址和临时变量,而且往往往栈里压入数据和弹出数据都需要时间。并且,递归组严重的问题就是调用栈溢出,因为每个进程中的栈容量有限,当递归次数过多时会超过最大栈容量。
此时我们在控制台执行
console.time()
Fibonacci(40)
console.timeEnd()
得到执行时间为1195ms(具体时间根据不同情况有所不同,根据自己执行的数据判断即可,下同),Oh My God 这也太久了,虽然我们解决了问题,但是我想如果数据量大你也绝对不会用这种低效的算法。
此时我们画出斐波那契求第十个数前面的几次调用
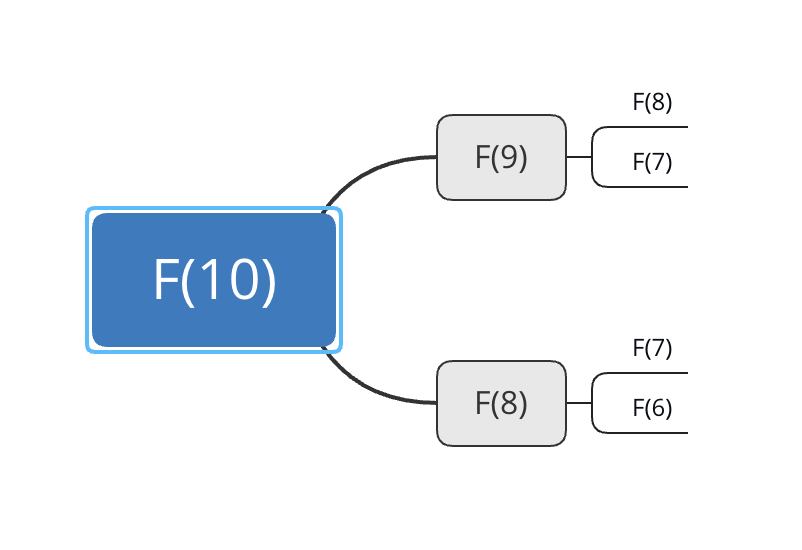
我们不难发现,内部存在一些重复的计算比如在F(9)中也计算的F(7),在F(8)中也计算了F(7),如果继续向下写也会存在更多的重复计算,所以计算量会根据n的变大而急剧变大,此时这种递归的时间复杂度是以n的指数呗递增的,如果你想试试,你可以把刚上例中的40改为100之后你就可以给自己一个放松的时间,喝一杯:coffee:,之后再来看是否执行完毕吧。
通过缓存数组来减少重复计算
function FibonacciWithMemory(n, memory) {
if (!memory) {
memory = []
}
if (n < 2) {
return n
}
if (!memory[n]) {
memory[n] = FibonacciWithMemory(n - 1, memory) + FibonacciWithMemory(n - 2, memory)
}
return memory[n]
}
此时我们通过一个缓存数组来缓存一些我们已经计算过的数据来减少重复计算,此时我们在控制台执行下面的代码:
console.time()
FibonacciWithMemory(40)
console.timeEnd()
得到时间只为0.014ms了,这减少的程度真的是有够多,此时我们“得寸进尺”地尝试我们上面不敢执行的100来试试
console.time()
FibonacciWithMemory(100)
console.timeEnd()
得到时间也只有0.028ms,此时我们想,还能不能继续优化呢?我们想到了,虽然我们优化了执行时间,但是递归带来的空间损耗并没有得到减少,例如我们如果把100改成10000,会直接栈溢出,所以我们思索一番后,我们决定使用动态规划的循环来试着减少空间消耗。
使用动态规划的解法
function FibonacciIterative(n) {
if (n < 2) {
return n
}
// 记录索引值
let i = 2
// 记录前一个值
let pre = 1
// 记录当前值
let current = 1
// 记录结果
let result = 0
// 从下往上计算 类推得到第n项的值
while(i++ < n) {
result = pre + current
pre = current
current = result
}
return result
}
此时我们没有使用递归,而是直接在一次调用中在函数内部的循环来计算结果,我们在控制台中执行
console.time()
console.log(FibonacciIterative(100))
console.timeEnd()
得到执行时间为0.14ms此时我们发现相比较缓存的递归我们执行时间加倍了,但是相比较于第一种递归还是我们能够接受的,此时我们来执行
console.time()
console.log(FibonacciIterative(10000))
console.timeEnd()
此时我们发现并没有报栈溢出的错误,但因为过大,控制台会输出Infinity,得到的执行时间为0.4ms,这依然在我们的可接受范围内!
总结
递归和循环的不同解法的时间效率会大相径庭。第一种递归的解法虽然简洁美观,但是时间消耗和空间消耗都过于高了,所以我们在实际的开发中也不会使用。第二种递归算法通过对计算结果进行缓存,大大减少了重复计算量,使时间消耗降低了很多,但还是存在空间方面的限制,存在栈溢出问题。第三种使用动态规划用循环实现,极大地降低了空间消耗,同时时间消耗相比于第二种虽然有所增加但是比起第一种递归还是有大幅度的减少。因此在实际的开发中我们更倾向于使用动态规划来解决。
在写递归时我们要记住几条准则:
- 只要有可能,就要使用记忆化「缓存」。
- 调用次数有可能过大,改用动态规划使用循环实现。
- 当存在栈溢出问题时,也可以尝试使用尾递归方法来进行优化。
更多内容: