决策树的损失函数

按照ID3或C4.5算法生成的决策树，可能对训练数据集有比较好的准确度，但是对未知数据的预测能力却不一定比较好，因为在训练过程中为了拟合训练数据而构造了很复杂的决策树的话，就会产生过拟合。解决这一问题的方法就是对决策树进行剪枝。

剪枝的目的是为了同时兼顾模型对训练集的拟合程度以及减少模型的复杂度来提高预测能力，那就不能仅仅使用信息增益来判别，还要加入带有模型复杂度的项对过于复杂的模型进行惩罚。

在这里定义决策树的损失函数(代价函数)：

设数的叶节点个数为|T|,t是T的叶节点，该叶节点有个样本，其中k类的样本有个，k=1,2,3,…K,Ht(T)为叶节点上t的经验熵，α>=0为参数,则决策树学习的损失函数可以定义为：

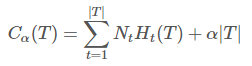
其中经验熵为：

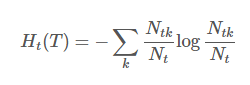
解释

损失函数计算的是每个叶节点的样本数和每个叶节点的经验熵的乘积的累加和最终加上以叶节点个数为基础的惩罚项，经验熵就是之前介绍计算数据集D的经验熵的公式。

为什么每个叶节点可以计算经验熵呢，叶节点不是都属于同一类吗？其实每个叶节点并不一定都属于同一个类，因为在树的生成过程中，生成叶子节点的条件并不仅仅是划分到子数据集只剩下一个类，如果小于某个信息增益(ID3)或信息增益比(C4.5)的话，也会直接生成叶节点，这个时候按照子数据集中占比最大的类作为叶子节点的类别

对于来说，左半边表示的训练数据的误差，也就是训练数据的拟合程度，而|T|表示模型复杂度，α来控制两者之间的关系，相当于一个惩罚系数。当α确定以后，剪枝的策略就是使得损失函数最小化。可以看出，决策树生成学习局部的模型，而决策树剪枝学习整体的模型。

决策树的损失函数最小化相当于正则化的极大似然估计 决策树的剪枝算法： 输入：生成算法产生的整个树T，参数α： 输出：修建后的子树Tα （1） 计算每个结点的经验熵 （2） 递归地从树的叶结点向上回缩

设一组叶结点回缩到其父结点之前与之后的整体树分别为TB与TA，其对应的损失函数值分别为与，如果

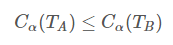
则进行剪枝，即将父结点变为新的叶结点。(3)返回(2)，直至不能继续为止，得到损失函数最小的子树。