定义
计数排序是一种非基于比较的排序算法,其空间复杂度和时间复杂度均为O(n+k),其中k是整数的范围。基于比较的排序算法时间复杂度最小是O(nlogn)的。该算法于1954年由 Harold H. Seward 提出。
算法步骤
- 找出待排序的数组中最大和最小的元素
- 统计数组中每个值为i的元素出现的次数,存入数组C的第i项
- 对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加)
- 反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1
排序示例
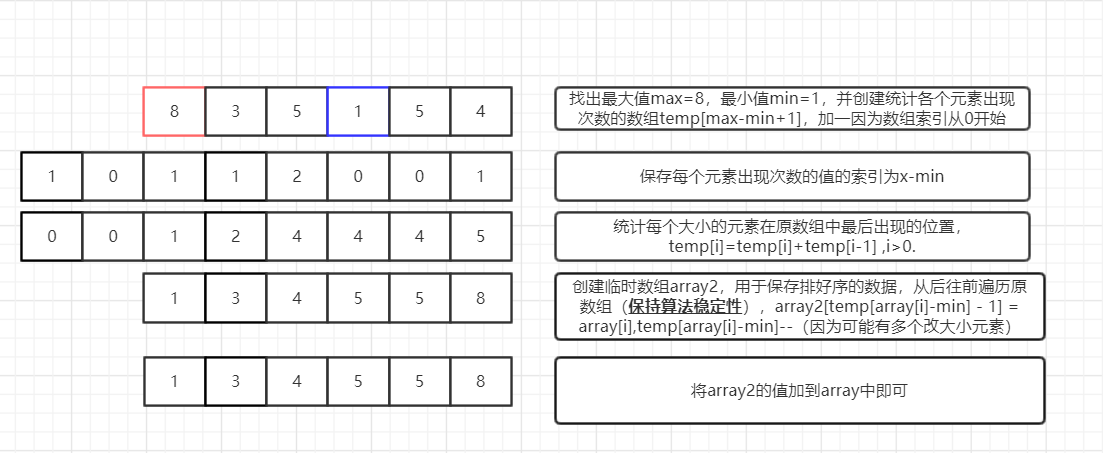
- 算法稳定性是指排序前A在B前,排序后A还在B前,而从后往前排序,就是为了保证算法的稳定性。
- 此算法不适合不知道大概范围的数据,否则会占用大量内存。
时间复杂度
首先需要遍历一次Array,找最大最小数,然后需要统计各个元素的出现次数,还要统计各个相同元素最后出席那的我位置(主要是用到临时数组temp),最后排序,所以时间复杂度为3O(n) + O(n+k),n+k为遍历临时数组temp的时间.
稳定性
该算法是稳定算法
代码实现
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace Algorithm.DataStructure.Sort
{
class CountingSort:SortData
{
public CountingSort():base()
{
name = name = "-======================计数排序法";
}
public override void Sort(int[] array)
{
base.Sort(array);
int min = GetMin(array);
int max = GetMax(array);
int[] temp = new int[max - min + 1];
for(int i = 0;i<array.Length;i++) //统计每个元素出现次数
{
temp[array[i] - min]++;
}
for(int i= 1;i< temp.Length;i++) //统计每个大小的元素最后应该出现的位置,应为从后往前排
{
temp[i] += temp[i - 1];
}
int[] array2 = new int[array.Length];
for(int i= array.Length - 1;i>= 0;i--) //排序
{
array2[temp[array[i] - min] - 1] = array[i];
temp[array[i] - min]--;
}
for (int i = 0; i < array.Length; i++)//将排序好的数据加到array中
{
array[i] = array2[i];
}
}
public int GetMax(int[] array)
{
int max = int.MinValue;
for(int i = 0;i < array.Length;i++)
{
if(array[i]>max)
{
max = array[i];
}
}
return max;
}
public int GetMin(int[] array)
{
int min = int.MaxValue;
for (int i = 0; i < array.Length; i++)
{
if (array[i] < min)
{
min = array[i];
}
}
return min;
}
}
}