
开篇
又是一个愉快的周五晚上,突然想到近期学过的计算组成原理中对浮点数的讲解,于是趁着心情好,抓紧撸知识点,翻了一遍JavaScript程序设计、犀牛书和计算机的组成相关书籍,略有小成,分享一下,如有问题,大家可以相互交流,本文章重点讲述Javascript语言遵循的IEEE754规范,其他使用此规范的语言都与此一样,例如Python等
简介
我们知道在日常开发中,都会或多或少的用到小数进行运算,在进行小数运算时候,经常会发现页面中突然出现1.2000000000000002这种奇怪的结果,有丰富前端经验的同学都知道,哦,这个简单是因为精度问题,可以通过Number.prototype.toFixed来转换小数点后面的位数,例如
let n1 = 0.1, n2 = 0.2
let n3 = n1 + n2 //0.30000000000000004
n3.toFixed(2) // 注意,toFixed为四舍五入到此,问题解决了,皆大欢喜,那我们为什么不深入一下原理,为什么会出现这个问题呢,下面带大家来看一下我梳理的结果
定点数
先以Float32单精度为例,32位中,我们用 4 个比特来表示 0~9 的整数,32 个比特就可以表
示 8 个这样的整数,然后我们把最右边的 2 个 0~9 的整数,当成小数部分;把左边 6 个
0~9 的整数,当成整数部分。这样,我们就可以用 32 个比特,来表示从 0 到 999999.99
这样 1 亿个实数了。 这种编码就是BCD编码(Binary-Coded Decimal),应用场景就是超市、银行,基本满足了小数部分的运算,缺点是32位的空间能够表示的40亿数字,现在被缩短到了1亿
浮点数
上面的定点数的小数部分,能够表示的范围还是很小的,有没有一种可以表示很大或者很小的浮点数呢,答案肯定是有的,就是我们刚才上面提到的IEEE754,我们还是以Float32为例
我们先来看一下十进制的小数如何转换成二进制的小数,和整数的二进制表示采用“除以 2,然后看余数”的方式相比,小数部分转换成二进制是用 一个相似的反方向操作,就是乘以 2,然后看看是否超过 1。如果超过 1,我们就记下 1, 并把结果减去 1,进一步循环操作,截一张《深入浅出计算机原理》中的图
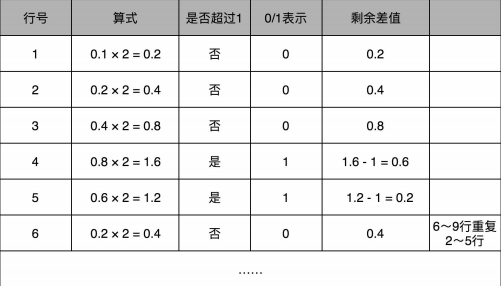
const n = 0.1
n.toString(2) // "0.0001100110011001100110011001100110011001100110011001101"由此可以看出,十进制0.1在转换二进制小数的过程中出现了死循环,后面的0011基本上是一个循环过程
我们再把它转成十进制,转换规则如下
let n = 0.1
let n1 = n.toString(2) //我们先取"0.0001"四位小数
let n2 = (0 * Math.pow(2, -1)) + (0 * Math.pow(2, -2)) + (0 * Math.pow(2, -3)) + (1 * Math.pow(2, -4))
console.log(n2) //0.0625,四位小数,精度已经丢失得到的值是一个近似值,搞清楚了这个,我们接下来继续看,IEFFF754规范下,如何进行小数运算,原则就是先对 齐、再计算
具体大家可以去详细了解IEFFF754,里面会有符号位、指数位、有效位的讲解
总结
文章写的有点仓乱,对一些重点可能没涉及,以后会继续完善,这里强调一下,JavaScript数字小数精度为17位,如果转换为字符串,可以发现,最大为55位,也就是Float64双精度表示
let n = 0.1
n.toString(2) // 0.0001100110011001100110011001100110011001100110011001101 55位
Number(n.toString(2)) //0.00011001100110011001 17位文章内容参考《JavaScript高级程序设计》《JavaScript权威指南》《深入浅出计算机原理》以及网上大量博客。