多项式回归

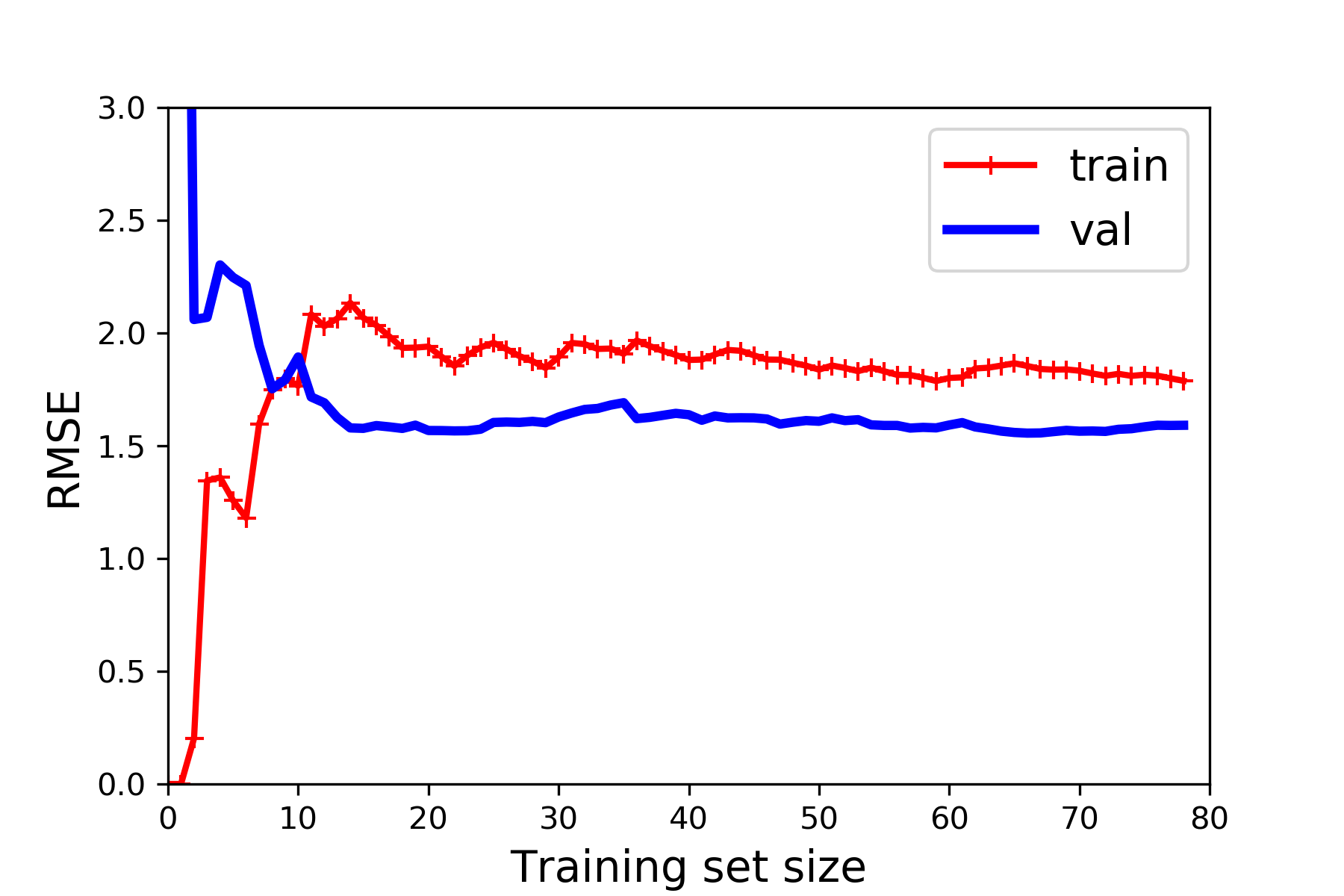
认识学习曲线 (learning curve)

假设我们有10000行数据,我们依次学习更多行的数据

方法:数据集大小为横轴,训练误差为纵轴,绘制训练集曲线和验证集曲线

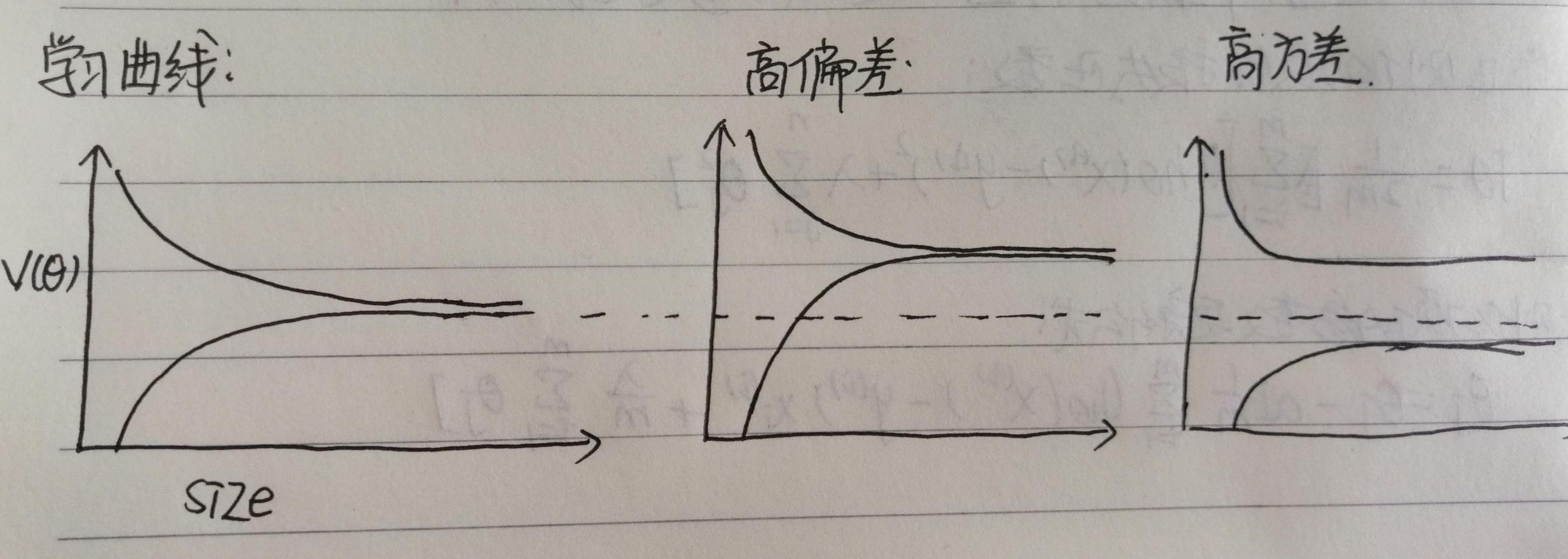
如图所示:

图1 为正常的学习曲线

图2 为高偏差的学习曲线(欠拟合)

图1 为高方差的学习曲线(过拟合)

偏差：是指一个模型的在不同训练集上的平均性能和最优模型的差异。偏差可以用来衡量一个模型的拟合能力。偏差越大，预测值平均性能越偏离最优模型。偏差衡量模型的预测能力，对象是一个在不同训练集上模型，形容这个模型平均性能对最优模型的预测能力。

方差：（ variance）描述的是一个模型在不同训练集上的差异，描述的是一个模型在不同训练集之间的差异，表示模型的泛化能力，方差越小，模型的泛化能力越强。可以用来衡量一个模型是否容易过拟合。 预测值的变化范围，离散程度，也就是离其期望值的距离。方差越大，预测结果数据的分布越散。方差用于衡量一个模型在不同训练集之间的关系，和最优模型无关。对象是不同训练集上的一个模型，表示选取不同的训练集，得出的模型之间的差异性。

记住：方差和偏差都是衡量模型的，方差表示选取不同的训练集，训练出模型的差异有多大，而偏差是指一个模型在不同训练集上的平均性能和最优模型的差异。

下面来实际看一看

首先准备工作 导入需要的包 给定一个图片的存储位置

import numpy as np
# 操作系统
import os
%matplotlib inline
# import matplotlib as mpl
import matplotlib.pyplot as plt
# 随机种子
np.random.seed(42)

# 保存图像

PROJECT_ROOT_DIR = "."
MODEL_ID = "linear_models"

def save_fig(fig_id,tight_layout = True): #定义一个保存图像的函数
    path = os.path.join(PROJECT_ROOT_DIR,"images",MODEL_ID,fig_id + ".png")
    print("Saving figure", fig_id)
    plt.savefig(path,format="png",dpi = 300)
# 把讨厌的警告过滤掉
import warnings
warnings.filterwarnings(action='ignore',message="^internal gelsd")

创建数据集

m = 100 
x = 6 * np.random.rand(m,1)-3  # 创建数据集的特征部分
y = 0.5 * x**2 + x + 2 + np.random.randn(m,1) # 创建数据集的标签部分

展示创建好的集合图像

plt.plot(x,y,"b.") # 把数据点画出来
plt.xlabel("$x_1$",fontsize =18)
plt.ylabel("$y$",fontsize =18,rotation = 0)
plt.axis([-3,3,0,10])
save_fig("quadratic_data_plot") # 保存图像
plt.show()

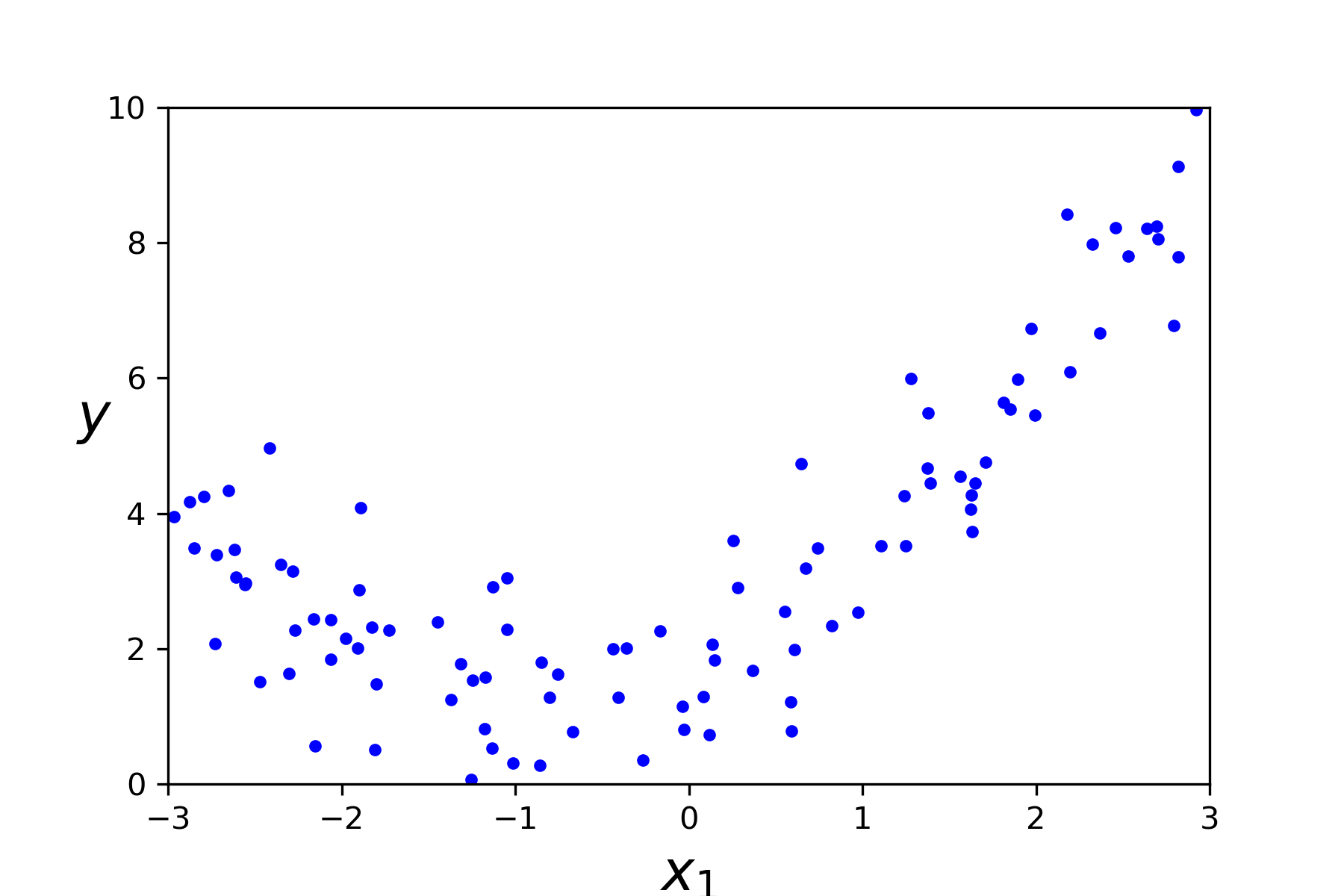
- 用多项式函数拟合测试数据集

from sklearn.linear_model import LinearRegression # 从线性模型里导入线性分类器
from sklearn.preprocessing import PolynomialFeatures # 从预处理包中导入多项式特征处理模块
poly_features = PolynomialFeatures(degree = 2,include_bias=False) # 初始化多项式特征对象
x_poly = poly_features.fit_transform(x) # 转化原始特征为多项式特征
lin_reg = LinearRegression() # 初始化一个线性分类器
lin_reg.fit(x_poly,y) # 分类器拟合多项特征
lin_reg.intercept_,lin_reg.coef_  # 获取参数

画出拟合函数图像

x_new = np.linspace(-3,3,100).reshape(100,1)
x_new_poly = poly_features.transform(x_new)
y_new = lin_reg.predict(x_new_poly)

plt.plot(x,y,"b.") # 把数据点画出来
plt.plot(x_new,y_new,"r-",linewidth = 2,label = "Predictions")
plt.xlabel("$x_1$",fontsize =18)
plt.ylabel("$y$",fontsize =18,rotation = 0)
plt.legend(loc="upper left",fontsize = 14)
plt.axis([-3,3,0,10])
save_fig("quadratic_predictions_plot") # 保存图像
plt.show()

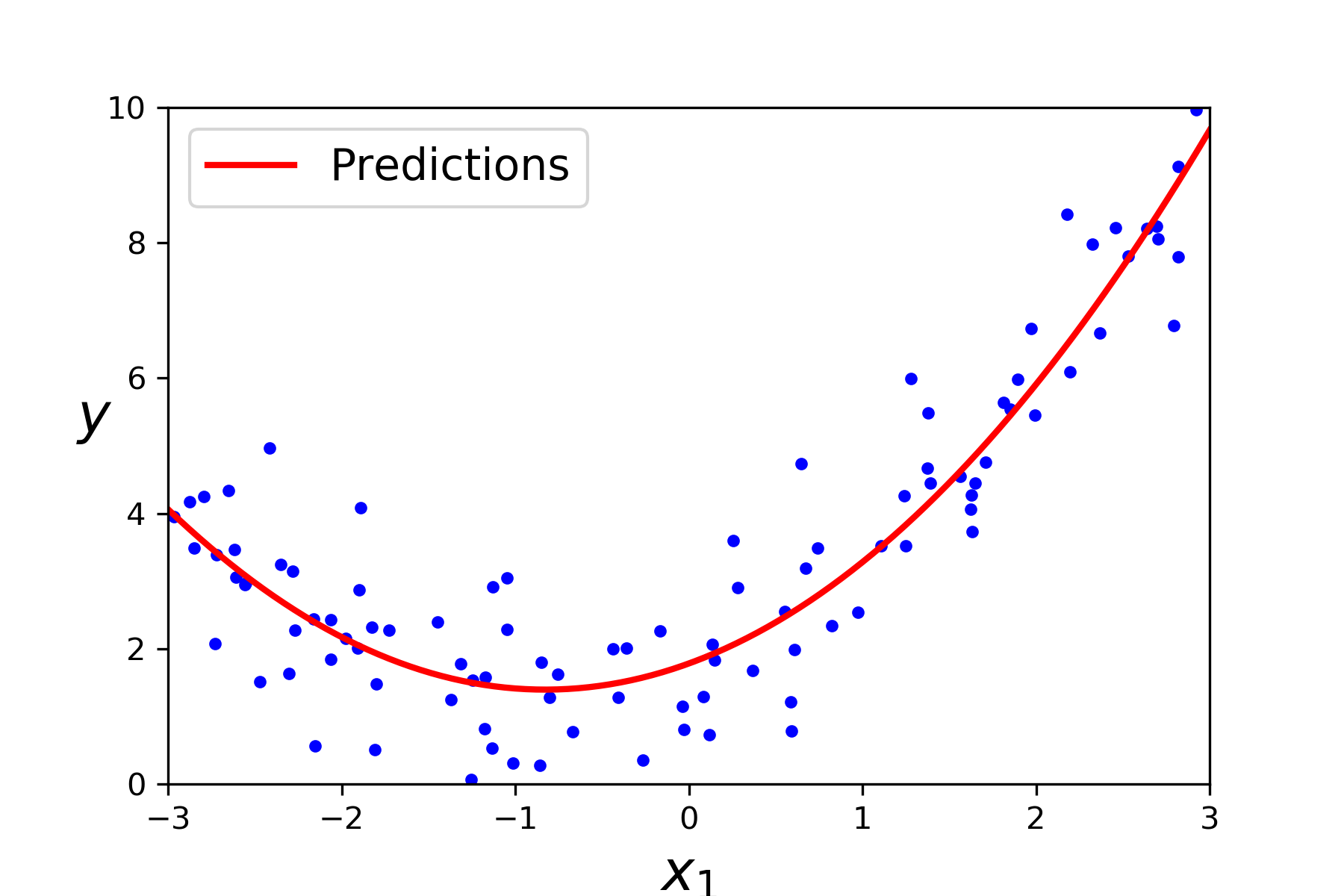
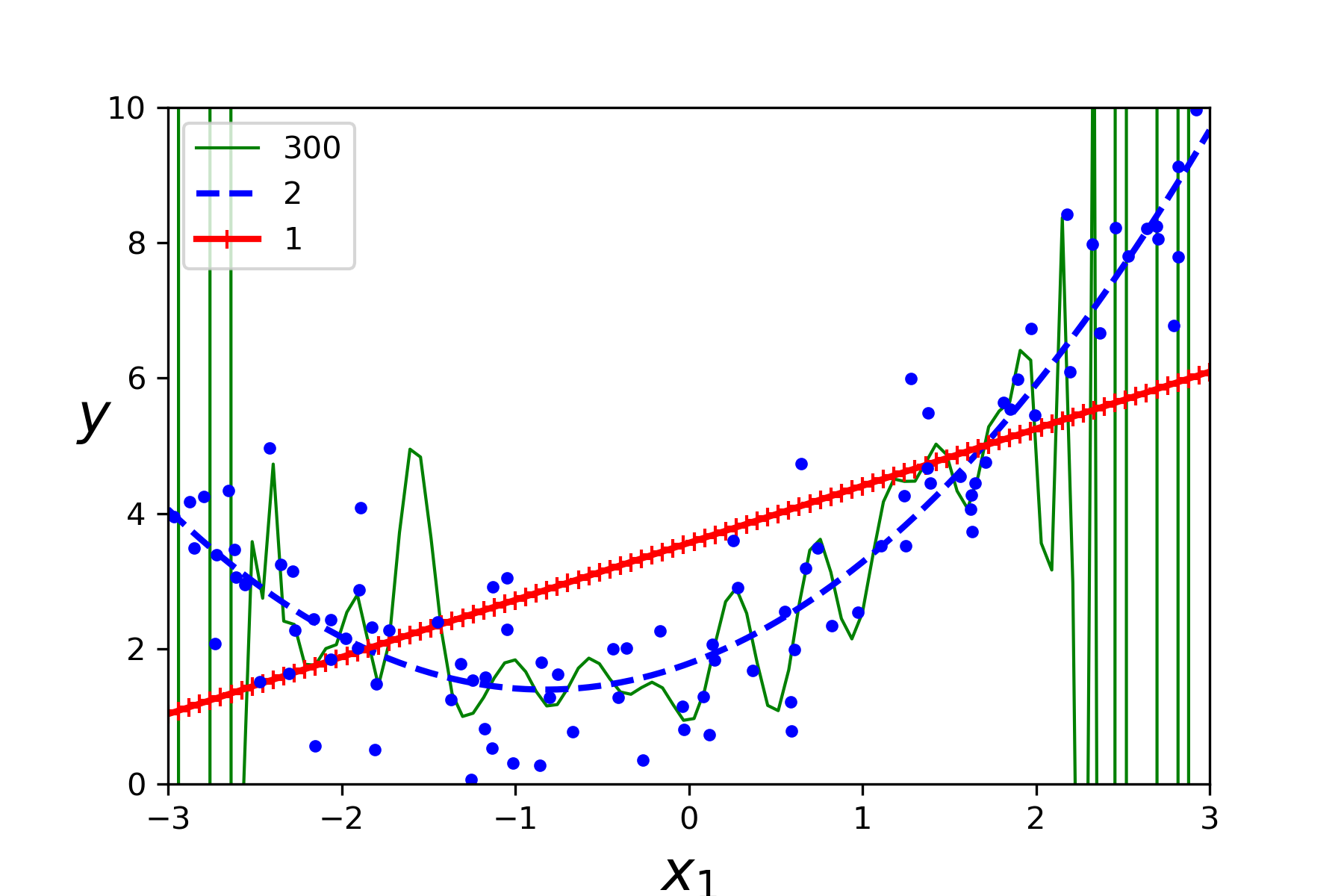
- 分别用1次方,2次方,300次方来拟合数据集曲线

from sklearn.preprocessing import MinMaxScaler # 从预处理包中导入归一化处理模块
from sklearn.pipeline import Pipeline # 导入流水线处理模块
from sklearn.preprocessing import StandardScaler  # 从预处理包中导入标准化处理模块


from sklearn.preprocessing import StandardScaler
# 导入流水线处理模块
from sklearn.pipeline import Pipeline

# 遍历三种画图方式
for style, width, degree in (("g-", 1, 300),("b--", 2, 2),("r-+", 2, 1)) :
    # 初始化多项式特征对象
    polybig_features = PolynomialFeatures(degree=degree, include_bias=False)
    std_scaler = StandardScaler() #数据标准化
    mm_scaler = MinMaxScaler()
    lin_reg = LinearRegression() #初始化线性分类器
    polynomial_regression = Pipeline([
        ("polybig_features", polybig_features), #pipeline 第一步 处理特征
        ("std_scaler", std_scaler), #标准化数据
        ("lin_reg", lin_reg), #初始化线性回归器
        
    ])
    polynomial_regression.fit(x,y) # 训练模型
    y_newbig = polynomial_regression.predict(x_new) # 预测数据
    # 画拟合好的3曲线中的一个
    plt.plot(x_new, y_newbig, style, label=str(degree), linewidth = width)


plt.plot(x,y,"b.", linewidth=3) #画原始数据点
plt.legend(loc = "upper left")
plt.xlabel("$x_1$",fontsize = 18)
plt.ylabel("$y$",rotation =0,fontsize = 18)
plt.axis([-3,3,0,10])
save_fig("high_degree_polynomials_polt")
plt.show()

- 画学习曲线图像

# 从度量包里导入均方误差
from sklearn.metrics import mean_squared_error 
# 从模型选择包里导入数据集切分模块
from sklearn.model_selection import train_test_split

定义学习曲线函数

def plot_learning_curves(model, x, y):
    # 切分数据集, 训练集80%, 验证集20%, 指定随机种子
    x_tarin,x_val,y_tarin,y_val = train_test_split(x, y, test_size = 0.2, random_state = 42)
    train_errors = [] #收集训练误差
    val_errors = [] #收集验证误差
    for m in range(1, len(x_tarin)): #遍历训练数据集
        model.fit(x_tarin[:m],y_tarin[:m]) #拟合数据
        y_tarin_predict = model.predict(x_tarin[:m]) # 预测测试集的值
        y_val_predict = model.predict(x_val)# 预测验证集的值
        # 计算真实值和训练集预测值之间的均方误差并收集
        train_errors.append(mean_squared_error(y_tarin[:m],y_tarin_predict))
        # 计算真实值和验证集预测值之间的均方误差并收集
        val_errors.append(mean_squared_error(y_val,y_val_predict))
        
        
    plt.plot(np.sqrt(train_errors), "r-+", linewidth=2, label="train")
    plt.plot(np.sqrt(val_errors), "b-", linewidth=3, label="val")
    plt.legend(loc = "upper right", fontsize=14)
    plt.xlabel("Training set size", fontsize=14)
    plt.ylabel("RMSE", fontsize = 14)

做图

lin_reg = LinearRegression() #初始化线性回归器
plot_learning_curves(lin_reg, x, y) #调用函数
plt.axis([0, 80, 0, 3])
save_fig("underfitting_learning_curves_plot")
plt.show()