Number数据类型
ECMAScript的Number类型的数值都是双精度数值。准确来说,是用IEEE754格式来存储数值的。
单精度数据存储方式
无论是单精度还是双精度在内存存储中都分为三个部分:
- 符号位(Sign) : 0代表正,1代表为负
- 指数位(Exponent):用于存储科学计数法中的指数数据,并且采用移位存储(移动的位数是基于二进制来移动的)
- 尾数部分(Mantissa):尾数部分,默认前面有一个1。如1.00101000100111....
对于单精度而言,数据使用32位进行存储。方式是1位符号位,8位指数位,23位尾数位。
对于双精度而言,数据使用64位进行存储。方式是1位符号位,11位指数位,52位尾数位。
其中单精度存储的方式大概如下

因为需要存储小数,所以指数位需要能表示出负数。8位指数位表示出负数有两种方法。
- 第一位用作符号位,8位表示范围是-127~127
- 没有符号位,8位表示的范围是0-255,然后默认真正表示的数为减去127(对半),最后的范围是-127~128。
可以看出来2比1要多一位显示,所以选2。
举一个例子:

符号位0,代表正数 指数位00000010,2^1=2,2-127=-125代表需要将二进制中的小数点向左移动125位。 小数位10000000....,代表二进制小数1.10000000000....
所以最后表示的是1.100000....向左移动125位,即0.000....00(小数点后有124个0)110000...,即2^-125+2^-126 约等于3.526483E-38
而双精度浮点数也是一样的道理。
精度
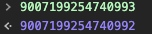
双精度的有效位是16位。也有说法是15~16。
因为双精度的尾数位有52位,我们假设尾数位都为1,先忽略指数位,得到的是1.111111...(52个1,此处是二进制)。算上指数位,不断往右移,我们不难发现小于11111...(53个1)的数都能准确的表达。但是如果继续往右移动1位,即11111....(53个1)0,这个0,我们无法控制它变为1,因为已经超出了尾数位能表示的范围,所以之后就失真了。所以1111...(53个1)是双精度能达到的最高精度,即2^53 - 1= 9007199254740991(十进制)。大于这个数的,可以尝试一下,输出的结果会失真。