和你一起终身学习,我是小学生。
今天和你一起看一道Leetcode题目:Maximum Profit in Job Scheduling
We have n jobs, where every job is scheduled to be done from startTime[i] to endTime[i], obtaining a profit of profit[i].
You are given the startTime , endTime and profit arrays, you need to output the maximum profit you can take such that there are no 2 jobs in the subset with overlapping time range.
If you choose a job that ends at time X you will be able to start another job that starts at time X.
Example 1:
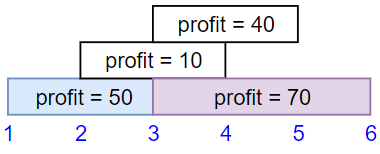
Input: startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70]
Output: 120
Explanation: The subset chosen is the first and fourth job.
Time range [1-3]+[3-6] , we get profit of 120 = 50 + 70.
Example 2:
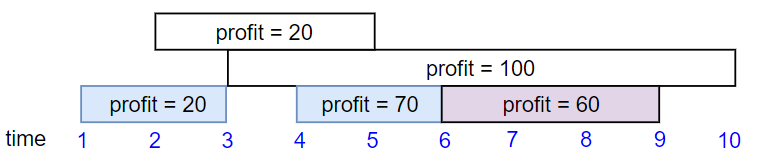
Input: startTime = [1,2,3,4,6], endTime = [3,5,10,6,9], profit = [20,20,100,70,60]
Output: 150
Explanation: The subset chosen is the first, fourth and fifth job.
Profit obtained 150 = 20 + 70 + 60.
Example 3:

Input: startTime = [1,1,1], endTime = [2,3,4], profit = [5,6,4]
Output: 6
Constraints:
1 <= startTime.length == endTime.length == profit.length <= 5 * 10^4
1 <= startTime[i] < endTime[i] <= 10^9
1 <= profit[i] <= 10^4
大致意思是让我们找在没有Job时间重合的情况下,最多能赚多少钱💰。
对于一个好久没有刷题的人来说,刚看到还是有些懵逼。下面是我解题的心路历程。希望对那些和我一样的菜鸟能有所帮助。
破题
我首先想到的是,一个Job对于最优解来说,只有两种情况:
- 最优解包括这个Job
- 最优解不包括这个Job
如果最优解包括这个Job,那么它就不能包括和这个Job时间有重叠的其他Job。如果最优解不包括这个Job,那么它就对于这道题无关轻重。
进一步来说,如果我们想知道前n个jobs最多能赚多少钱(maxProfit(n)),那么只可能有两种情况:
- 最优解包括最后那个Job n:profit[n] + maxProfit(n之前和n不重叠的jobs)
- 最优解不包括最后那个Job n:maxProfit(n - 1)
对于前n - 1个jobs来说,想要找到最多赚多少也是一样的。只需要继续往前看就好了。通过这个,一个简单的recursion 方法大致就出现了。
解题
在能顺利写出第一个没有优化的recursion算法之前,还有一个问题没有解决:
怎么样找到离 job n 最近的没有时间重叠的 job,来继续递归?
想要解决这个问题,我们需要解决两个小问题:
- 离 job n 最近
- 没有时间重叠
离 job n 最近:需要对结束时间(endTime)由小到大排序
没有时间重叠:需要针对 job list 从最晚到最早,找到第一个job,它的endTime是小于等于 job n 的startTime
因为题目给的三个array,很难在对endTime array排序之后,相对应的对startTime和profit arrays排序,所以我想构建一个新的数据结构:
private static class Job {
int startTime;
int endTime;
int profit;
public Job(int startTime, int endTime, int profit) {
this.startTime = startTime;
this.endTime = endTime;
this.profit = profit;
}
}
之后就可以排序了(高手们不要介意我笨拙的语法水平,下面代码只针对解决目前所遇到的问题)
Arrays.sort(jobs, (job1, job2) -> {
if (job1.endTime < job2.endTime) {
return -1;
} else if(job1.endTime > job2.endTime) {
return 1;
} else {
return 0;
}
});
有了排好序的array,我们就可以找到离n最近的没有时间重叠的那个job了
private int findNearestJobWithoutOverlap(Job[] jobs, Job j) {
for (int i = jobs.length - 1; i >= 0; i--) {
if (j.startTime >= jobs[i].endTime) {
return i;
}
}
return -1;
}
解决了这些问题,递归方法就能写出来了
public int jobScheduling(int[] startTime, int[] endTime, int[] profit) {
Job[] jobs = new Job[startTime.length];
for (int i = 0; i < startTime.length; i++) {
jobs[i] = new Job(startTime[i], endTime[i], profit[i]);
}
Arrays.sort(jobs, (job1, job2) -> {
if (job1.endTime < job2.endTime) {
return -1;
} else if(job1.endTime > job2.endTime) {
return 1;
} else {
return 0;
}
});
return maxProfit(jobs, startTime.length - 1);
}
private int maxProfit(Job[] jobs, int i) {
if (i == 0) {
return jobs[0].profit;
}
if (i < 0) {
return 0;
}
return Math.max(maxProfit(jobs, i - 1), maxProfit(jobs, findNearestJobWithoutOverlap(jobs, jobs[i])) + jobs[i].profit);
}
总体来说,这个方法的runtime complexity是2的n次方,n是array的长度。
出于好奇,我尝试submit我的答案到leetcode,结果过了15个test case,然后就超时了。
优化
看起来和高手们差距还不小(捂脸)。
当算maxProfit时,很多时候我们传入的i的值是重复的。这样就重复的递归一些本来就知道答案的方法。于是最简单的方法是用一个HashMap来存放我们已经知道的maxProfit。
聪明的小伙伴早就看出来这是一道动态规划题。谢谢你迁就我到现在。
简单修改过后,这个是动态规划的方法:
class Solution {
private Map<Integer, Integer> profitMap = new HashMap<>();
public int jobScheduling(int[] startTime, int[] endTime, int[] profit) {
Job[] jobs = new Job[startTime.length];
for (int i = 0; i < startTime.length; i++) {
jobs[i] = new Job(startTime[i], endTime[i], profit[i]);
}
Arrays.sort(jobs, (job1, job2) -> {
if (job1.endTime < job2.endTime) {
return -1;
} else if(job1.endTime > job2.endTime) {
return 1;
} else {
return 0;
}
});
return maxProfit(jobs, startTime.length - 1);
}
private int maxProfit(Job[] jobs, int i) {
if (i == 0) {
return jobs[0].profit;
}
if (i < 0) {
return 0;
}
if (!profitMap.containsKey(i)) {
profitMap.put(i, Math.max(maxProfit(jobs, i - 1), maxProfit(jobs, findJobIndexByStartTime(jobs, jobs[i])) + jobs[i].profit));
}
return profitMap.get(i);
}
private int findJobIndexByStartTime(Job[] jobs, Job j) {
for (int i = jobs.length - 1; i >= 0; i--) {
if (j.startTime >= jobs[i].endTime) {
return i;
}
}
return -1;
}
private static class Job {
int startTime;
int endTime;
int profit;
public Job(int startTime, int endTime, int profit) {
this.startTime = startTime;
this.endTime = endTime;
this.profit = profit;
}
}
}
相交于之前,runtime complexity下降到了O(n)。不过因为是用space来代偿速度,space cost是O(n)。
之后我又点了submit,答案被接受了。只是
Runtime: 1405 ms, faster than 5.04% of Java online submissions for Maximum Profit in Job Scheduling.
在寻找离n最近的没有时间重叠的那个job时候用的是for loop,如果换binary search,结果可能会更快一些。剩下的就留给小伙伴来做啦。(懒)
希望这篇散文能对你有所帮助。也希望高手们能留言告诉我还有哪些地方可以改进。感激。