带你入门排序算法冒泡排序其实就是遍历一个数组，比较当前元素和下一个元素，如果当前元素比下一个大，向上冒泡。下次循环继续上

冒泡排序

原理

冒泡排序其实就是遍历一个数组，比较当前元素和下一个元素，如果当前元素比下一个大，向上冒泡。下次循环继续上面的操作，不循环已经排好序的数。其实你可以理解成每次比较两个数，把大的放后面，这样一趟就可以把最大的数放在最后面了。

举个例子，未排序数组：[7, 5, 3, 1, 9, 4, 6, 8, 2]

第1趟数组： (9) [5, 3, 1, 7, 4, 6, 8, 2, 9]

第2趟数组： (9) [3, 1, 5, 4, 6, 7, 2, 8, 9]

第3趟数组： (9) [1, 3, 4, 5, 6, 2, 7, 8, 9]

第4趟数组： (9) [1, 3, 4, 5, 2, 6, 7, 8, 9]

第5趟数组： (9) [1, 3, 4, 2, 5, 6, 7, 8, 9]

第6趟数组： (9) [1, 3, 2, 4, 5, 6, 7, 8, 9]

第7趟数组： (9) [1, 2, 3, 4, 5, 6, 7, 8, 9]

第8趟数组： (9) [1, 2, 3, 4, 5, 6, 7, 8, 9]

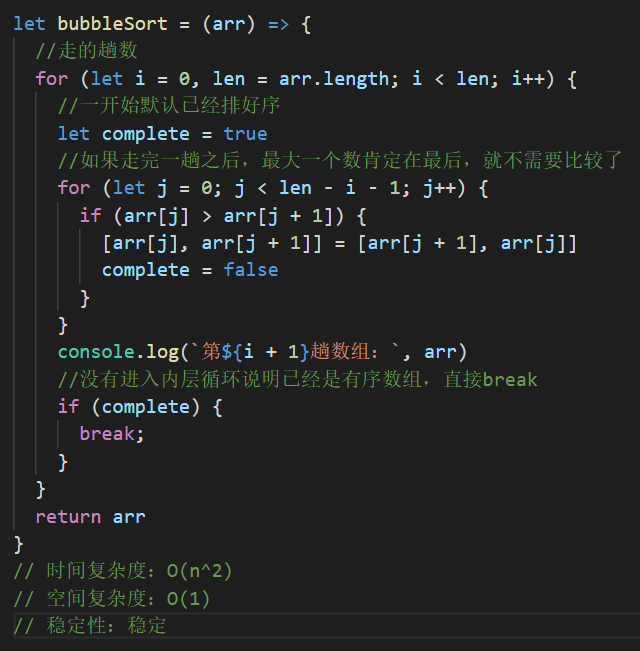
代码

首先第一步，你要思考清楚冒泡原理；第二步在大脑里面构建思路，第三步构建代码。第三部往往都是代码功底比较差的小伙伴（像我QAQ），很难去实现的。没有捷径，多写多思考。

小优化：当一次循环没有发生冒泡，说明已经排序完成，停止循环。

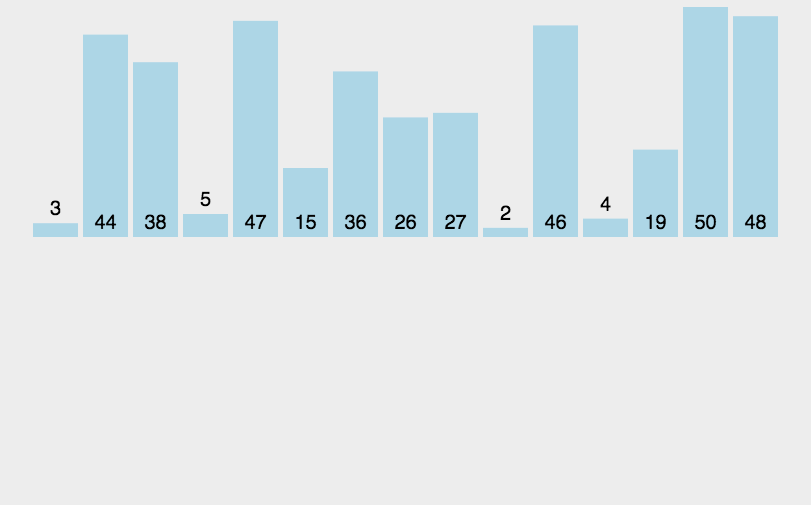
插入排序

原理

将左侧序列看成一个有序序列，每次将一个数字插入该有序序列。

插入时，从有序序列最右侧开始比较，若比较的数较大，后移一位。

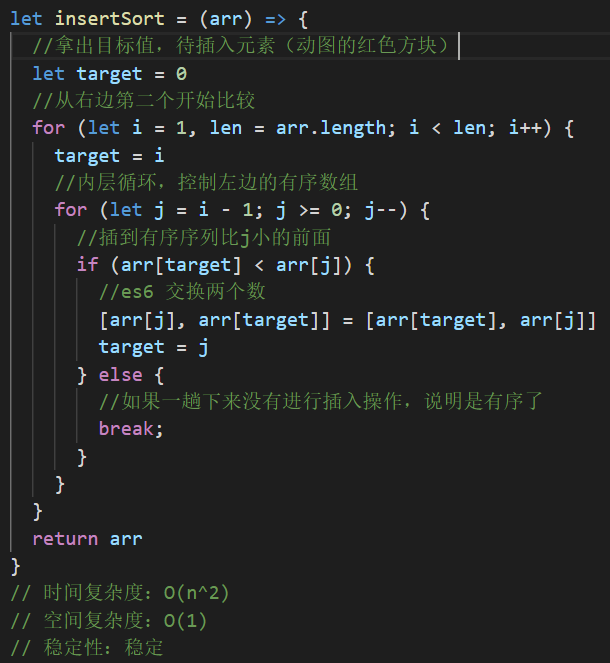
代码

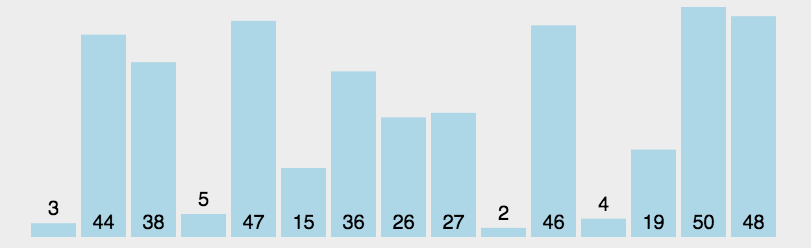
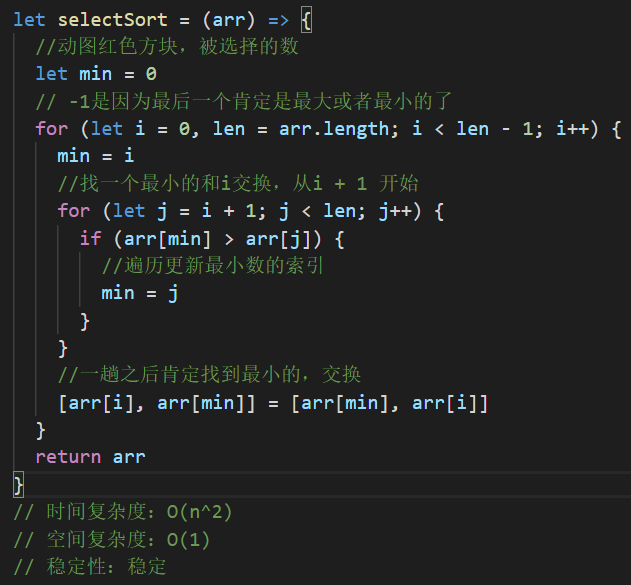
选择排序

原理

每次循环选取一个最小的数字放到前面的有序序列中。（这和冒泡很像）

代码

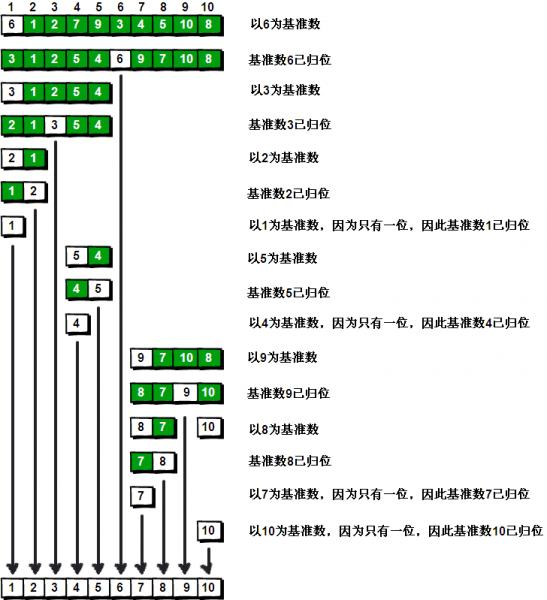
快速排序

原理

快速排序，利用了分治的思想（将问题分解成一些小问题递归求解）

通过选取一个基准值，小的放左边，大的放右边，然后递归求解；

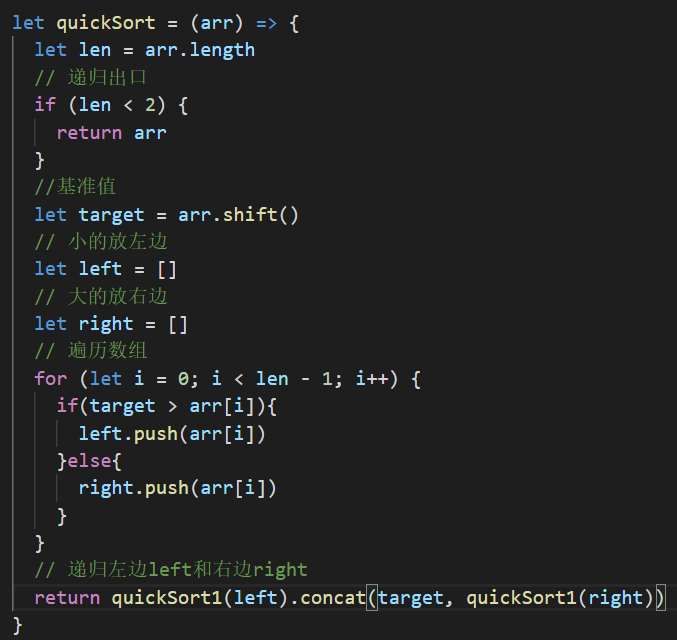
代码

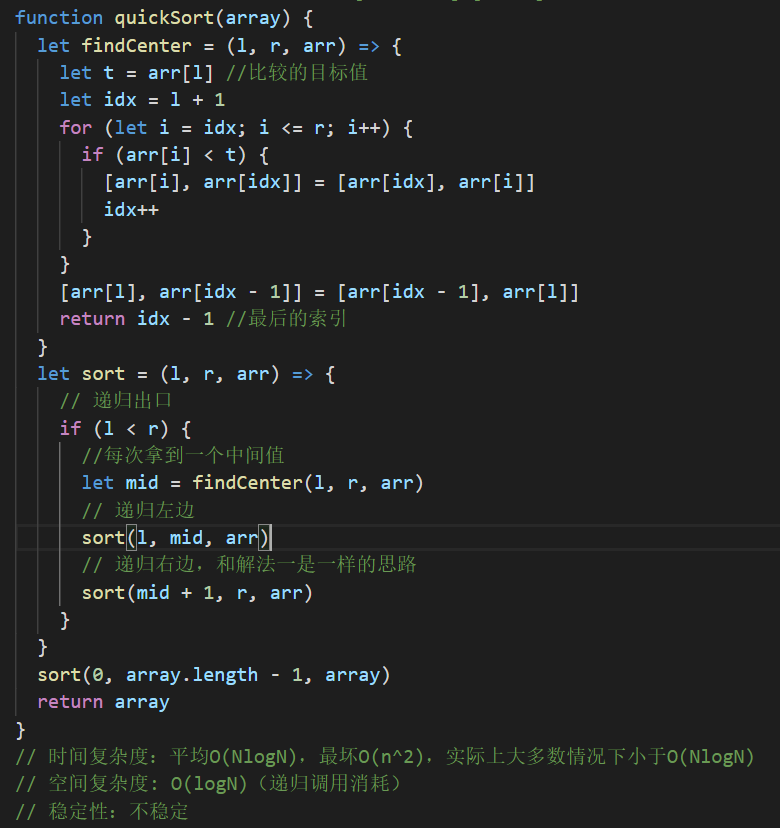
有能力的同学可以尝试第二种解法（推荐）

利用两个指针，一个指针指向起始目标值，另一个指针idx指向要交换的值

满足条件条件 idx < t, 则把小的放到左边，idx右移一位；

最后一趟之后 t [小于t] [idx, 大于t]

要把 t 和 idx - 1 互换，变成 [小于t, t] [大于t], 并且返回 t 的索引进行下一轮递归

归并排序

原理

归并排序，利用分治的思想实现的排序方法。

一直往下分解，分到小于2，然后就反过来一直合并。

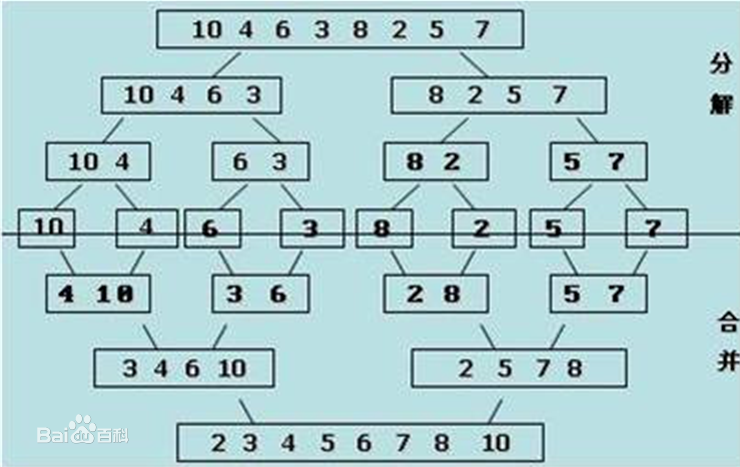
代码

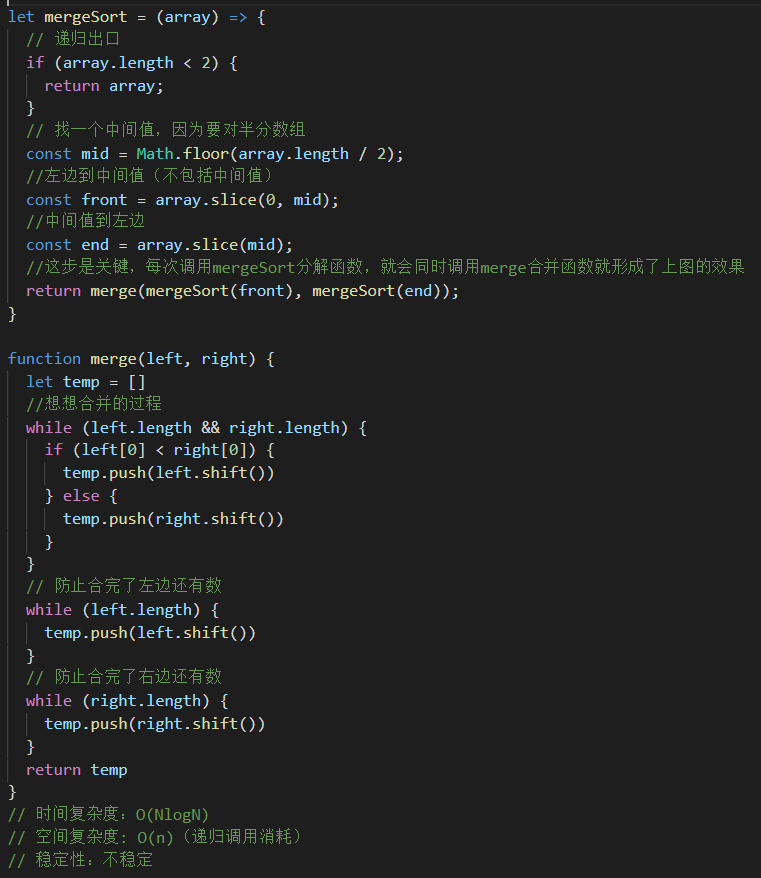
有能力的同学可以尝试不用temp临时数组的写法

堆排序

堆排序相对以上几种排序来说比较难理解，但是不要怕，把复杂问题拆分成若干小问题就可以解决了。

原理

1.创建一个大顶堆，大顶堆的堆顶一定是最大的元素。

2.交换第一个元素和最后一个元素，让剩余的元素（除了最后一个）继续调整为大顶堆。

3.从后往前以此和第一个元素交换并重新构建，排序完成。

那么我们先来完成上面的思路

关键是怎么构建一个大顶堆呢？首选你要明确以下几个概念

1.堆是一个完全二叉树（不懂完全二叉树的小伙伴一定要先百度）。

2.因为堆是完全二叉树，所有刚好可以用一个数组表示，索引代表第几个节点。

3.比如第i个节点，它的父节点是 Math.floor((i - 1) / 2)，既 (i - 1) / 2 取整，左子树是2*i+1， 右子树是2*i+2。

4.堆最重要的一个特性是在任意节点 i 中，它都比自己的左右节点都大。

到这里，其实你抓住关键点3和4；就可以构建一个大顶堆

构建大顶堆的原理

从最后一个父节点开始，依次从最后面的父节点到堆顶（树根），不断的进行比较；比较父节和两个儿子节点这三个节点的大小，把这三个节点最大节点变成父节点。就完成了大根堆的构建了

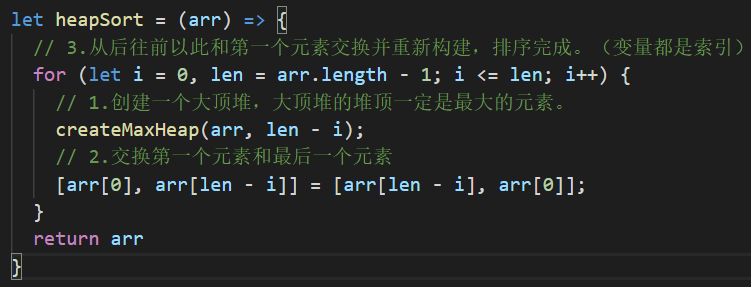
代码

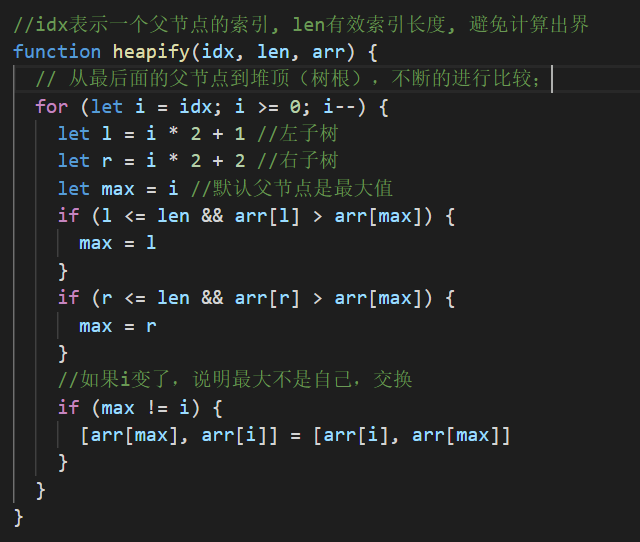
构建大顶堆

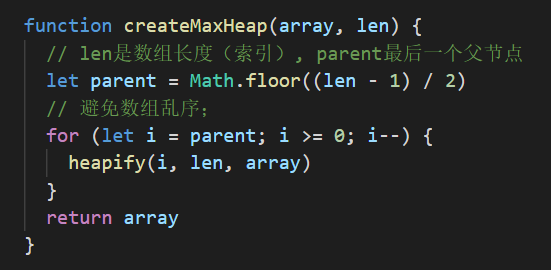
合并代码

上面是最简单粗暴的方法，但是这样子做会存在一定的效率问题，这个留个同学们思考，贴一个我最后自己思考练习的版本。

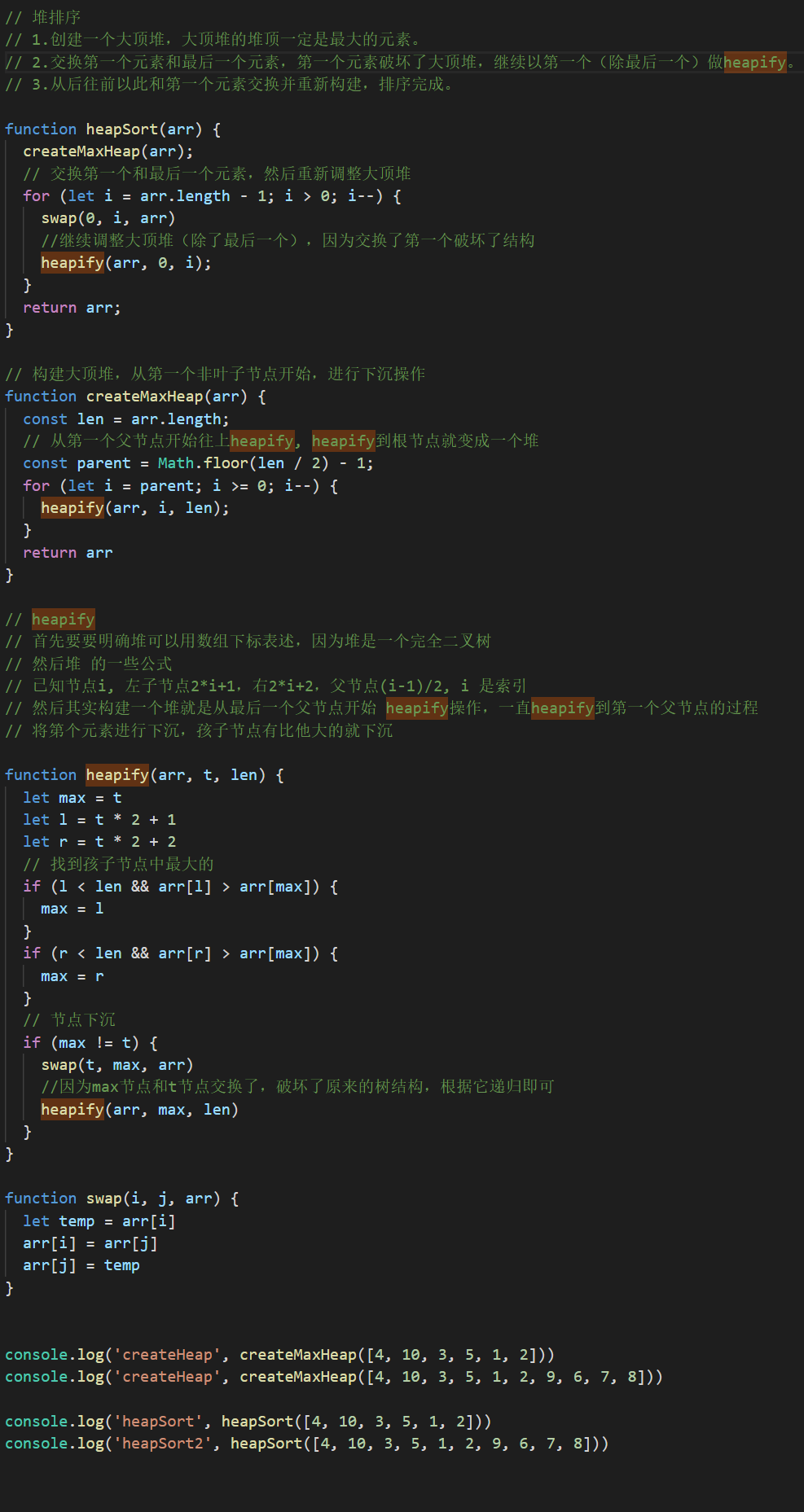
最后

自己做的一个小笔记，难免避免出现错漏，点个赞再走呗。QAQ

参考大腿文章，链接：www.conardli.top/docs/