题目描述
在一个国家仅有1分,2分,3分硬币,将钱N分兑换成硬币有很多种兑法。请你编程序计算出共有多少种兑法。
动态规划
基本思想
动态规划的基本思想与分治法类似,也是将待求解的问题分解为若干子问题,按照顺序求解子问题。与分治法不同的是,适合动态规划的求解问题,进过分解后得到的子问题往往不是相互独立的,即存在重叠子问题。由于动态规划解决的问题多数有重叠子问题的特点,为了减少重复用计算,对每一个子问题只求解一次,然后将不同阶段的不同状态都保存在一个二维数组中。
三要素
- 最优子结构:确定求解的问题具有最优子结构性质,即问题的最优解包含了其子问题的最优解。
- 状态转移方程:转态转移就是根据子问题(上一阶段)状态和决策来导出本问题(当前阶段)的状态,确定了决策方法,就可以写出转态转移方程。
- 边界条件:状态转移方程是一个递推式,需要一个递推的终止条件或边界条件来最终解出动态规划问题。
钱币兑换求解思路
如果我们令table[i][j]表示用前i种硬币构造 j 分钱的总方法数,table[i][j]的表示的总的兑换方法大致可以分成两种:
- 第 i 种硬币一个都不选,都不参与兑换
- 第 i 种硬币至少有一个参与兑换 可以明显的发现这个问题具有最优子结构的性质,同时也能写出转态转移方程:
table[i][j] = table[i-1][j] + table[i][j-val[i]]
其中val[i]表示第i种硬币的面值,这里val[0]=0,val[1]=1,val[2]=2,val[3]=3, 我们以一个n = 4的例子来讲解填表的过程,这样我们的问题就变成了一个填表的问题,这里的边界条件是table[i][0]=1, i=0~4。根据转态转移方程和边界情况将table[][]的值填完,最终便可以得到原问题的解。
这里第一列的物理意义表示用前 i 种硬币兑换0分钱的兑换方式都是1种,第一行表示利用面额为0 硬币兑换0~4分钱的方法分别是1,0, 0,0,0种方法。
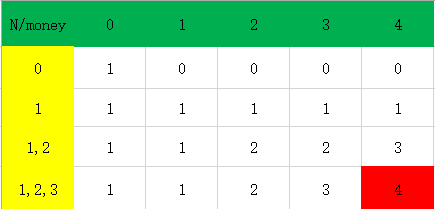
从这个表格和求解思路可以简单的发现这个方法的时间和空间的复杂度都是:
O(n*l),其中n是钱币的数目,l是硬币的种数
下面附上代码
/**
* 全量table表,这里val = {1, 2, 3}
*/
public static int fullDpTableExchange(int num, int[] val) {
int length = val.length;
int[][] table = new int[length+1][num+1];
for (int i=0; i<=length; i++) {
table[i][0] = 1;
}
for (int i=1; i<=length; i++) {
for (int j=1; j<=num; j++) {
if (j < val[i-1]) {
table[i][j] = table[i-1][j];
} else {
table[i][j] = table[i-1][j] + table[i][j-val[i-1]];
}
}
}
return table[length][num];
}
滚动数组空间压缩法1
虽然上面的解法的空间复杂度是O(n*l),但实际上,对于状态转移方程,考虑到每个table[i][j]都仅和table[i-1][j]和table[i][j-val[i]]有关,那么可以通过利用滚动数组的方式,将table[i][j]所需要空间压缩至table[2][j],从而将空间复杂度降为O(l),空间复杂度的系数为2。
举个例子,我们将table[0][j]状态存在二维表的第0行,接着推出table[1][j]对应的值,并将table[1][j]的状态存放于二维表的第1行。再接着推出table[2][j]的状态时,table[0][j]的状态已经没有保存意义了,因此直接将table[2][j]的状态保存到二维表的第0行,并以此类推,使数组空间得到循环利用。
我们以一个n = 4的例子来讲解滚动覆盖的过程
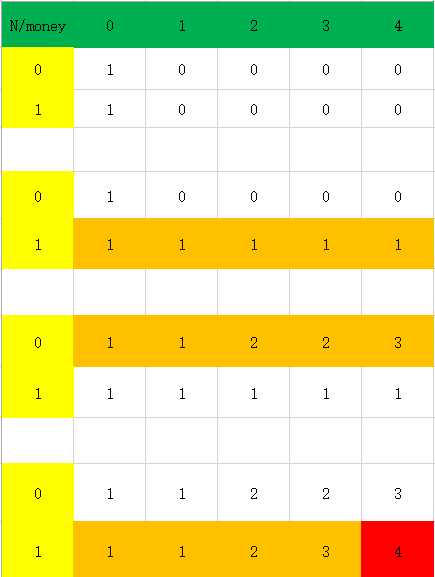
下面附上代码:
/**
* 2维table数组,这里val = {1, 2, 3}
*/
public static int twoDimDpTableExchange(int num, int[] val) {
int length = val.length;
int[][] table = new int[2][num+1];
for (int i=0; i<2; i++) {
table[i][0] = 1;
}
for (int i=1; i<=length; i++) {
int idx = (i - 1) % 2;
for (int j=1; j<=num; j++) {
if (j < val[i-1]) {
table[i%2][j] = table[idx][j];
} else {
table[i%2][j] = table[idx][j] + table[i%2][j-val[i-1]];
}
}
}
return table[1][num];
}
滚动数组空间压缩法2
进一步理解状态转移方程和滚动数组法后,可以发现这里可以进一步将二维数组压缩成一维数组。由于table[i%2][j]的计算只需要table[idx][j] 和 table[i%2][j-val[i-1]]的值。我们可以将状态转移方程改写成一维数组形式,值得注意的是由于于计算table[idx][j]的时候需要使用同迭代轮下的table[i%2][j-val[i-1]]值,所以在一维状态转移方程的计算是增序的:
table[j] = table[j] + table[j-val[i]]
从而将空间复杂度降为O(l),空间复杂度的系数为1。
下面附上代码:
public static int oneDimDpTableExchange(int num, int[] val) {
int length = val.length;
int[] table = new int[num+1];
table[0] = 1;
for (int i=1; i<=length; i++) {
for (int j=1; j<=num; j++) {
if (j < val[i-1]) {
table[j] = table[j];
} else {
table[j] = table[j] + table[j-val[i-1]];
}
}
}
return table[num];
}
各位看官,觉得总结的有点用的,点个赞呗~ 参考文献: