[数据结构]从JS数组到链表浅谈数据结构前言作为一个前端,我们习惯了用数组存储某些数据并调用数组的各种api,但是我们真

前言

作为一个前端, 我们习惯了用数组存储某些数据并调用数组的各种api, 但是我们真的懂数组么, 本文是我, 一个前端渣渣和数据结构小白, 从js数组到链表做的一些关于数据结构的探究

先看一个有趣的小实验

// 操作计数
let operationCount = 0

// 定义响应式, 劫持数组读写
function defineReactive(data, key, value) {
  Object.defineProperty(data, key, {
    enumerable: true,
    configurable: true,
     get () {
      operationCount++
      return value
    },
     set (newVal) {
      operationCount++
      value = newVal
    }
  })
}

// 观察数组的每个元素
function observe(data) {
  Object.keys(data).forEach(key => {
    defineReactive(data, key, data[key])
  })
}

// 创建一个size为100的数组并用0填充
let array = new Array(100).fill(0)
observe(array)

// 我们也可以用代理劫持数组的读写操作
// array = new Proxy(new Array(100).fill(0), {
//   get (target, key, receiver) {
//     operationCount++
//     return Reflect.get(target, key, receiver)
//   },
//   set (target, key, value, receiver) {
//     operationCount++
//     return Reflect.set(target, key, value, receiver)
//   }
// })

// 打印操作计数
function logOperationCount (caseName, fnName, ...args) {
  operationCount = 0
  array[fnName](...args)
  console.warn(caseName + ' operationCount: ', operationCount)
}

logOperationCount('首部增', 'unshift', 0)

logOperationCount('尾部增', 'push', 0)

logOperationCount('首部删', 'shift')

logOperationCount('中间删', 'splice', 50, 1)

logOperationCount('尾部删', 'pop')

operationCount = 0
array[50] = 1
console.warn('改 operationCount: ', operationCount)

operationCount = 0
array[50]
console.warn('查 operationCount: ', operationCount)

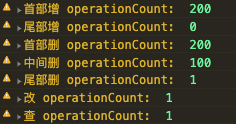
从上面的输出结果我们可以看到, 从首部做增删操作以及从中间做删除操作, 实际需要的读写操作数是跟数组的长度程线性关系的, 改和查需要的操作数是1

数据结构的分类

为什么会出现上面现象呢, 这里我们要引入一个概念,即物理数据结构与逻辑数据结构, 这个跟CSS中的物理像素与逻辑像素很类似, 物理数据结构是在计算机硬件中真实存在的, 逻辑数据结构是在物理数据结构的基础上实现的一个抽象的概念

	线性数据结构	非线性数据结构
逻辑数据结构	数组, 链表, 栈, 队列	树, 图
物理数据结构	数组	链表

物理上的线性数据结构是内存中连续的有序的存储空间, 就像排排坐的一群小朋友们一样, 一个挨着一个, 而且通过叫小朋友的名字, 马上就可以找到这个小朋友

回到上面的代码, JS的数组其实一种逻辑的线性数据结构, 在底层给我们做了一些如扩容(resize)的封装,就好像我们把一个小朋友放到某个位置时, 这个小朋友后面的小朋友都得往后挪一挪, 我们让某个小朋友从座位上出来后, 这个小朋友后面的小朋友都得往前挪一挪

物理上的非线性数据结构是内存中非连续的乱序的存储空间, 各个元素在内存中的位置是随机分配的,它可以有效的利用零散的内存空间, 它就像一个藏宝图一样, 只能从第一个线索挨个的去寻找下一个线索

链表的每个节点保存了数据, 也保存了它相邻节点的地址

实现一个简单的链表

// 链表节点
class LinkedListNode {
  data: any
  next: LinkedListNode
  constructor(data) {
    this.data = data
  }
}

// 范围检查
function checkRange (target: Object, propertyName: string, propertyDescriptor: PropertyDescriptor): PropertyDescriptor {
  const rawFunction = propertyDescriptor.value
  propertyDescriptor.value = function (...args: any[]) {
    const size = target['getSize'].apply(this)
    let index
    if (propertyName === 'insert') {
      index = args[1]
      if (index < 0 || index > size) {
        throw new RangeError(`param index: ${ index } is out of range`)
      }
    } else {
      index = args[0]
      if (index < 0 || index >= size) {
        throw new RangeError(`param index: ${ index } is out of range`)
      }
    }
    return rawFunction.apply(this, args)
  }
  return propertyDescriptor
}

// 链表
class LinkedList {

  // 头部指针
  private head: LinkedListNode
  // 尾部指针
  private tail: LinkedListNode
  // 容量
  private size: number = 0

  // 增操作
  @checkRange
  insert (data: any, index: number = this.size) {
    const insertedNode: LinkedListNode = new LinkedListNode(data)
    if (this.size === 0) {
      // 链表没有节点
      this.head = insertedNode
      this.tail = insertedNode
      this.tail.next = null
    } else if (index === 0) {
      // 从头部插入
      insertedNode.next = this.head
      this.head = insertedNode
    } else if (this.size === index) {
      // 从尾部插入
      this.tail.next = insertedNode
      this.tail = insertedNode
      this.tail.next = null
    } else {
      // 从中间插入
      const prevNode: LinkedListNode = this.get(index - 1)
      insertedNode.next = prevNode.next
      prevNode.next = insertedNode
    }
    ++this.size
  }

  // 删操作
  @checkRange
  remove (index: number): LinkedListNode {
    let removedNode: LinkedListNode = null
    if (index === 0) {
      // 从头部删除
      removedNode = this.head
      this.head = this.head.next
    } else if (index === this.size - 1) {
      // 从尾部删除
      const secondLastNode: LinkedListNode = this.get(this.size - 1)
      removedNode = secondLastNode.next
      secondLastNode.next = null
      this.tail = secondLastNode
    } else {
      // 从中间删除
      const prevNode: LinkedListNode = this.get(index - 1)
      removedNode = prevNode.next
      prevNode.next = prevNode.next.next
    }
    --this.size
    return removedNode
  }

  // 改操作
  @checkRange
  set (index: number, value: any) {
    const currentNode = this.get(index)
    currentNode.data = value
  }

  // 查操作
  @checkRange
  get (index: number): LinkedListNode{
    let res: LinkedListNode = this.head
    for (let i = 0; i < index; ++i) {
      res = res.next
    }
    return res
  }

  // 从头部到尾部打印所有的链表节点
  print () {
    let currentNode: LinkedListNode = this.head
    while(currentNode) {
      console.dir(currentNode)
      currentNode = currentNode.next
    }
  }

  getSize (): number {
    return this.size
  }

}

const myLinkedList: LinkedList = new LinkedList()

myLinkedList.insert('a')
myLinkedList.insert('b')
myLinkedList.set(1, 'c')
myLinkedList.print()

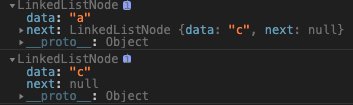
上面实现的是一个单向链表, 如果链表的每个节点有prev指针, 就能回溯它的上一个节点, 可实现双向链表, 如果尾结点的next指针指向头节点, 可实现循环链表

大O表示法

O即operation操作

大O表示法可衡量运行程序所需要的时间, 即时间复杂度, 也可表示运行程序所需要额外开辟的空间, 即空间复杂度

O(1)

在数组里查找一个元素通过索引, 即物理数据结构中数组指针的偏移量, 即可找到该元素, 需要的操作数是常数级的, 时间复杂度为O(1)
程序运行时多使用一个变量, 开辟常数空间, 空间复杂度为O(1)

O(n)

前面的数组实验中, 增删元素需要的操作数跟数组的长度是程线性关系的, 时间复杂度为O(n)
程序运行时多使用一个辅助数组, 空间复杂度为O(n)

O(n^2)

冒泡排序双重循环, 时间复杂度为O(n^2)
程序运行时多使用一个辅助二维数组, 空间复杂度为O(n^2)

O(logn)

通过二分查找法查找长度为n的有序数组中的某个元素, 需要 $\log_2^n$ 次操作, 因为如下数学公式所以可忽略底数, 时间复杂度为O(logn)

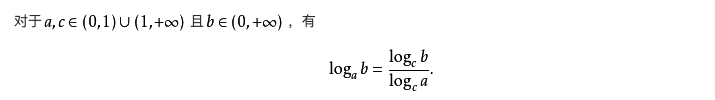
其他复杂度

其他复杂度还有O(nlogn)等

数组与链表的复杂度比较

	增	删	改	查
数组	O(n)	O(n)	O(1)	O(1)
链表	O(1)	O(1)	O(1)	O(n)

数组适合读操作多的场景
链表适合写操作多的场景