leetcode:11.container-with-most-water

题目描述

给定 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点(i,ai) 。在坐标内画 n 条垂直线，垂直线 i的两个端点分别为(i,ai) 和 (i, 0)。找出其中的两条线，使得它们与x轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器，且n的值至少为 2。

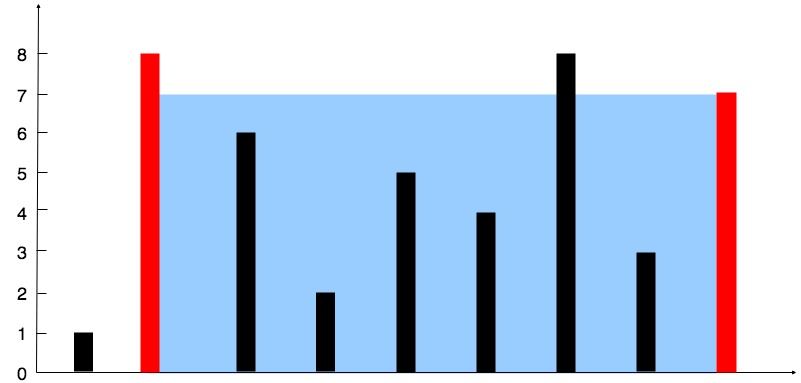
解题思路

暴力解法永远都是万能的，找到所有的容器并计算面积 双指针法：数组头尾各置一指针，并不断向内移动短板指针，过程中记录下面积最大值即为要求结果。 解释。记S(i,j)为某一过程中指针位置对应的容器面积，不放令指针i对应的高度小于指针j对应的高度，则，S(i, j-1),S(i, j-2)......S(i, i+1)，面积均小于S(i,j)。即在不断移动短板指针的过程中得到的结果一定包含最大值。证毕

代码

JS版

var maxArea = function (height) {
  let i = 0, j = height.length - 1;
  let max_area = 0;
  while(i < j){
    let area = (j - i) * Math.min(height[i], height[j]);
    max_area = Math.max(max_area, area);
    if(height[i] < height[j]){
      i++;
    }else{
      j--;
    }
  }
  return max_area;
};

PY版

class Solution(object):
    def maxArea(self, height):
        """
        :type height: List[int]
        :rtype: int
        """
        left = 0
        right = len(height) - 1
        maxArea = 0
        while left < right:
            b = right - left
            if height[left] < height[right]:
                h = height[left]
                left += 1
            else:
                h = height[right]
                right -= 1
            area = b*h
            if maxArea < area:
                maxArea = area
        return maxArea