插入排序
1.算法思想
构建有序的序列,选择一个未排序的元素,在有序的序列中从后往前的扫描比较,
找到合适的位置插入。
比如:在打牌过程中,存在扑克序列 [ 10, 3 , 6, 4 ]
首先,拿起第一张扑克,于是手上有了 [ 10 ] ,
继续拿第二张扑克 3 ,和手中牌比较之后,插入其中,得到 [ 3, 10 ]
继续拿第三张扑克 6 ,比较之后插入,得到 [ 3, 6 , 10 ]
继续拿第四张扑克 4 ,比较之后插入,得到 [ 3, 4, 6, 10 ]
2.示例
现在存在一个数组 [ 3, 44, 38, 5, 47, 15 ]

首先手里先抓起第一张牌 3
再去抓起第二张牌 44 ,要和手里的牌 3 进行比较
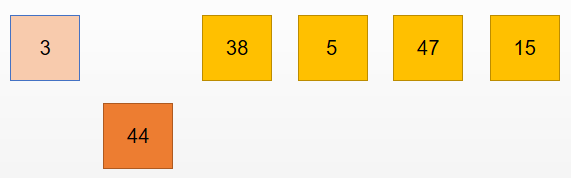
判断 3 < 44 ,所以不需要交换位置

继续抓起第三张牌 38 ,与手里的牌进行比较:
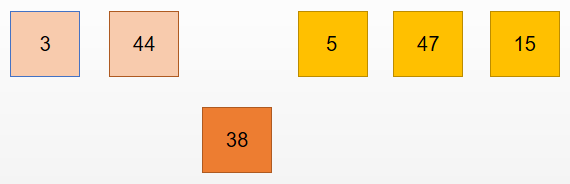
判断 44 > 38 , 交换位置:
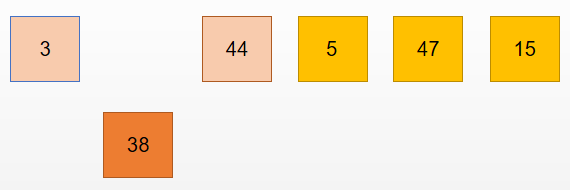
判断 3 < 38 , 所以不需要交换位置,此时就是 第三张牌 38 的位置

继续抓起第四张牌 5 并和手中牌进行比较:
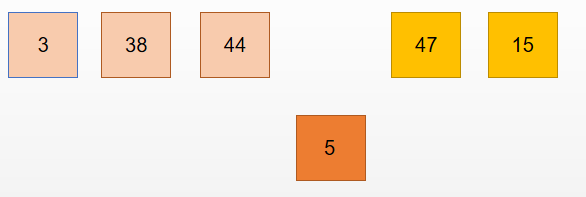
判断 44 > 5 , 交换位置:
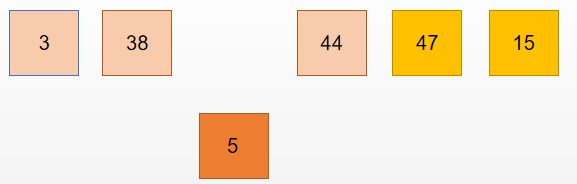
判断 38 > 5 , 交换位置:
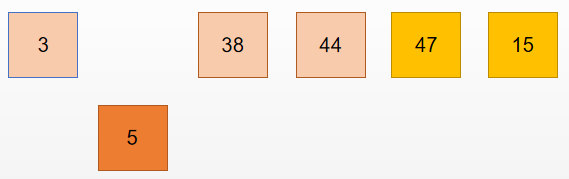
判断 3 < 5 ,所以不需要交换位置,此时就是第四张牌 5 的位置

继续抓取第五张牌 47 ,和手里的牌进行比较
判断 44 < 47 , 那么不需要再和前面的元素进行比较了,因为前面都是有序的。

继续抓起 第六张牌 15 ,继续和手里的牌进行比较
判断 47 > 15,交换元素的位置:
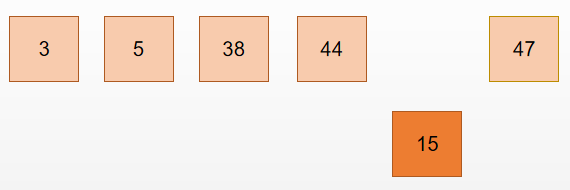
判断 44 > 15,交换位置:
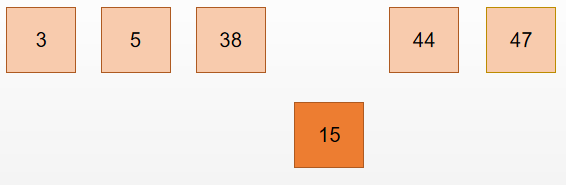
判断 38 > 15 , 交换位置:
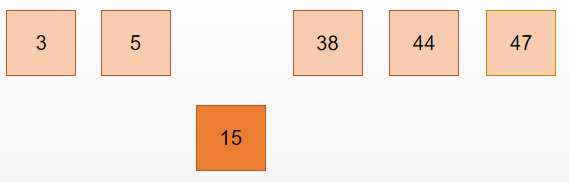
判断 5 < 15 , 不用交换位置,这样就确定了 15 的位置

此时 这个数组就通过插入排序完成了排序。
3.代码实现
现在让我们来看一看代码:
public static void main(String[] args) {
int[] arrs = new int[100];
for(int i = 0; i < 100; i++) {
arrs[i] = (int) (Math.random() * (100 + 1));
}
insertSort(arrs);
}
public static void insertSort(int[] a) {
int N = a.length;
for(int i = 1; i < N; i++ ) {
int temp = a[i];
for(int j =i - 1;j >= 0 && a[j] > temp; j-- ) {
a[j+1] = a[j];
a[j] = temp;
}
}
}
可以看到外循环从数组的第二个元素开始
而内循环则是将外循环选取的元素逐一和前面已经排序的元素进行比较
直到外循环结束
4.代码优化
这一段代码是可以优化的
可知 手中的牌是有序的,那么我们在为抓取的牌找寻合适的位置的时候,我们可以使用二分查找。
那么 让我们来看看代码:
public static void insertSort2(int[] a1) {
int N = a1.length;
for(int i = 1; i < N; i++){
int temp = a1[i];
int left = 0;
int right = i - 1; // 因为从 i -1 开始才是有序的数组
while(left <= right){
int middle = left + (right - left) / 2;
if(temp < a1[middle]){
right = middle - 1;
} else {
left = middle + 1;
}
}
// 将有序数组的元素后移
for(int j = i; j > left; j--){
a1[j] = a1[j-1];
}
a1[left] = temp;
}
}
可以看到 查找的方法用了 二分查找
让我们来看一下时间对比:
public static void main(String[] args) {
int[] arrs = new int[100000];
for(int i = 0; i < 100000; i++) {
arrs[i] = (int) (Math.random() * (100000 + 1));
}
long time= System.currentTimeMillis();
insertSort(arrs);
long time1 = System.currentTimeMillis();
System.out.println(" time : " + (time1 - time));
insertSort2(arrs);
System.out.println(" time1 : " + (System.currentTimeMillis() - time1));
}
结果:

从时间看出,优化查找方式对时间的提升还是有的。
5.时间复杂度
最坏情况:
整个数组都是逆序 那么 比较的次数 就是 1 + 2 + ... + N-1 = N(N-1) /2 ~ N^2 /2 次比较 每一次比较都要伴随着交换,所以有 N^2 /2 所以 时间复杂度就是 O( N^2 )
最好情况:
整个数组都是有序的 那么只需要 N-1比较 和 0次交换 所以时间复杂度是 O( N )
6.使用场景
首先要明白 什么是倒置 ?
比如 在 3,2,5,1 中,存在4对倒置:
有 3-2,3-1,2-1,5-1 。
存在倒置的数量较少的时候,也就是数组部分有序的情况下,插入排序的速度是要快于其他排序。