译者:王锐 转载至微信公众号:方凳雅集
译者按: 人工智能技术一直处于高速更迭中。良好的数学基础有助于你理解人工智能技术的进化,同时也能让你更深入地去理解并使用人工智能技术,而不是停留在AI技术的表面。另外,这样做也可以帮助你更好地去看待AI知识产权的问题。最后,职业规划方面,一旦你掌握了数据科学背后的数学基础,便可去从事更高端的AI和数据科学方面的工作。 本文将带你了解数据科学背后需要的数学知识,及其在机器学习算法中的应用。
文章翻译自https://www.dataquest.io/blog/math-in-data-science/

数学就像一头章鱼, 它有一只能够触及到每种学科的触手,虽然对某些学科只是轻轻拂过,但大部分学科都和数学有着不可分割的联系,数据科学属于后者。如果你想研究数据科学,你将必须先处理数学。如果你已经完成了数学学位或其他一些强调数据分析能力的学位,你可能需要知道你所学的东西是否是必要的。我知道我做到了。如果你
在这篇文章中,我们将探索研究数据科学意味着什么并讨论开始研究数据科学需要了解多少数据知识。我们从“数据科学”的实际含义开始吧!你可能会问几十个人然后获得几十个不同的答案!在Dataquest(译者注: 一个数据分析网站https://www.dataquest.io/),我们将数据科学定义为使用数据和高级统计数据进行预测的学科。这是一门专业学科,专注将杂乱无章的数据变得让人可以理解(尽管数据科学家正在解决的问题因雇主而异)。统计学是我们在该定义中提到的唯一数学学科,但数据科学也经常涉及数学中的其他领域。
学习统计数据是一个很好的开始,但数据科学也会使用算法进行预测。这些算法称为机器学习算法,总数达数百种。至于每种类型的算法需要多么高深的数学知识则不属于本文的范围,我们将讨论对于以下算法你需要掌握何种程度的数学知识。
- 朴素贝叶斯
- 线性回归
- Logistic回归
- 神经网络
- K-Means聚类
- 决策树
现在让我们来看看学习这些算法你需要掌握哪些数学知识!
朴素贝叶斯的量词
它们是什么:Naïve Bayes’ 的分类器是一系列基于共同原则的算法,即特定特征的值独立于任何其他特征的值。它们允许我们根据我们对相关事件的了解情况预测事件发生的概率。该名称来自贝叶斯定理,可以用数学方式编写如下:
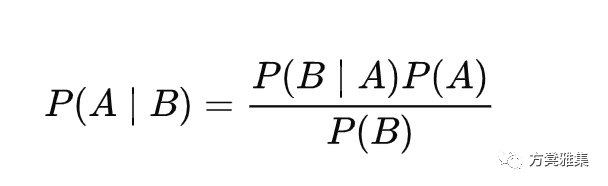
这里 A 和 B 是独立事件并且 P(A|B) 不能等于0.这看起来很复杂,但我们可以把它分解便于理解的三部分
- P(A|B)是条件概率。具体来说,是事件B发生后事件A发生的概率
- P(B|A)也是一个条件概率。具体来说,是事件A发生后事件B发生的概率
- P(A) 和 P(B)是A和B相互观察并相互独立的可能性。
我们需要的数学:如果你想要了解NaïveBayes的分类器算法的表面以及贝叶斯定理的所有用法,那么概率课程就足够了。要了解概率,您可以查看我们的概率和统计学课程。
线性回归
它是什么:线性回归是最基本的回归类型。它允许我们理解两个连续变量之间的关系。在简单线性回归的情况下,这意味着获取一组数据点并绘制可用于预测未来的趋势线。线性回归是参数化机器学习的一个例子。在参数化机器学习中,训练过程最终使机器学习算法成为一种数学函数,其最接近于它在训练集中找到的模式。然后可以使用该数学函数来预测未来的预期结果。在机器学习中,数学函数被称为模型。在线性回归的情况下,模型可以表示为:
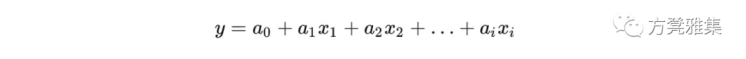
这里的a1,a2,a3...表示特定于数据集的参数值, x1, x2, ..., xñ 表示我们选择在上述模型中使用的变量, y表示目标。线性回归的目标是找到最佳描述特征列和目标列之间关系的最佳参数值。换句话说:找到最适合的数据,以便可以推倒它的趋势以预测未来结果。为了找到线性回归模型的最佳参数,我们希望最小化模型的残差平方和。残差通常被称为误差,它描述了预测值和真实值之间的差异。残差平方和的公式可表示为:
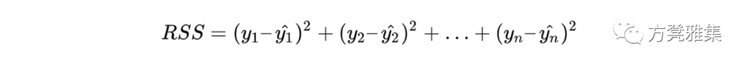
(这里 ÿ^ 是目标的预测值,y是真值。)
我们需要掌握的数学只是:如果你只想了解表面,基础统计学课程就可以了。如果你想要深入的概念理解,你可能需要知道派生的残差平方和的公式是什么,你可以在大多数高级统计课程中学到。
Logistic回归
它是什么:Logistic回归侧重于估计在因变量为二进制的情况下发生事件的概率(即,只有两个值,0和1表示结果)。与线性回归一样,逻辑回归是参数化机器学习的一个例子。因此,这些机器学习算法的训练过程的结果是最接近训练集中的模式的数学函数。但是,在线性回归模型输出实数的情况下,逻辑回归模型输出概率值。正如线性回归算法产生的线性函数模型一样,逻辑回归算法产生的逻辑函数模型。您可能还会听到它被称为sigmoid函数,它会压缩所有值以产生0到1之间的概率结果。
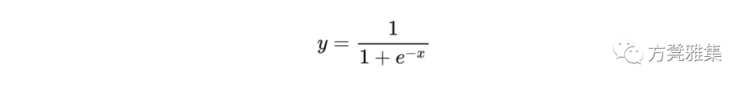
那么为什么sigmoid函数总是返回0到1之间的值?请记住,从代数中将任何数字提高到负指数与将该数字的倒数提高到相应的正指数相同。
我们需要掌握的数学知识:我们在这里讨论过指数和概率,你需要对代数和概率有充分的理解,以便对逻辑算法中发生的事情有所了解。如果你想深入了解它的概念,我建议学习概率论以及离散数学或实际分析。
神经网络
它是什么:神经网络是机器学习模型,它们受到人类大脑中神经元结构的极大启发。这些模型是通过使用一系列激活单元(称为神经元)构建的,以预测某些结果。神经元采取一些输入,应用转换函数,并返回输出。
神经网络擅长捕获数据中的非线性关系,并帮助我们完成音频和图像处理等任务。虽然存在许多不同类型的神经网络(递归神经网络,前馈神经网络,递归神经网络等),但它们都依赖于转换输入以生成输出的基本概念。
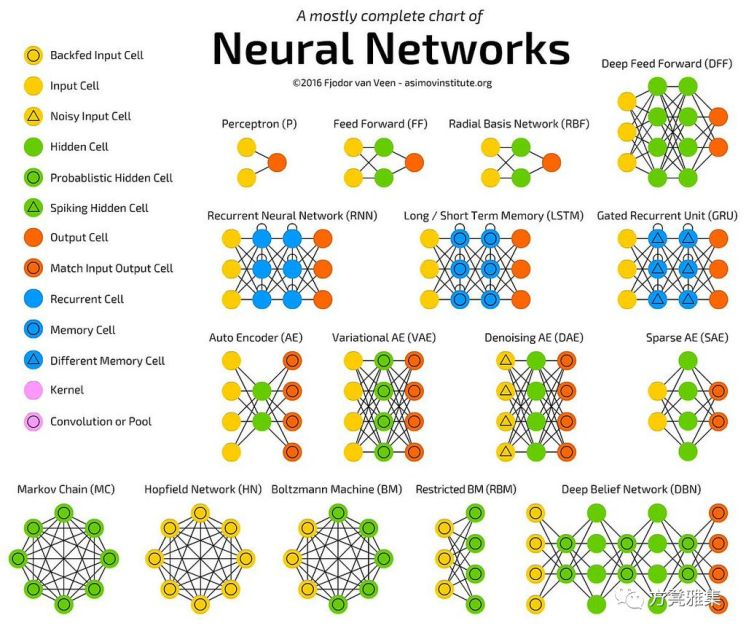
在查看任何类型的神经网络时,我们会注意到每一条线条,都将每个圆圈连接到另一个圆圈。在数学中,这就是所谓的图,一种由边缘连接的节点(表示为圆圈)组成的数据结构(表示为线条)。请记住,我们在这里引用的图与线性模型或其他方程的图不同。如果您熟悉旅行商问题,您可能熟悉图的概念。
神经网络的核心是一个系统,它接收一些数据,执行一些线性代数,然后输出一些答案。线性代数是理解神经网络中幕后发生的事情的关键。线性代数是关于线性方程的数学分支,如y=mx + b和他们通过矩阵和向量空间的表示。因为线性代数涉及通过矩阵表示线性方程,所以矩阵是你需要知道的基本思想,甚至可以开始理解神经网络的核心部分。矩阵是由数字,符号或表达式组成的矩形阵列,按行或列排列。矩阵按照行列排列,例如,以下矩阵

被称为3乘3矩阵,因为它有三行三列。
通过处理神经网络,每个特征都表示为输入神经元。要素列的每个数值都乘以表示输出神经元的权重向量。在数学上,该过程是这样写的:
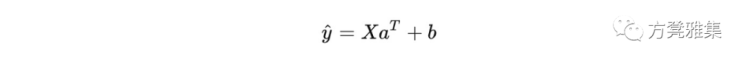
其中X是一个m*n的矩阵,m是输入神经元的数量,n是下一层神经元的数量。我们的权向量表示为a,aT是a的转置(译者注:转置矩阵),我们把偏差单位表示为b。
偏差单位是通过向左或向右移动S形函数来影响神经网络输出的单位,以便对某些数据集进行更好的预测。Transpose是一个线性代数术语,它的意思是行成为列,列成为行。我们需要取a的转置,因为第一个矩阵的列数必须等于第二个矩阵的行数。例如,如果我们有3×3 矩阵和权重向量是一个 1×3向量,我们不能直接将其相乘,因为三个不等于一个。但是,如果我们采取的转置1×3 矢量,我们得到一个 3×1 向量,我们就可以成功地将矩阵与向量相乘。
在所有特征列和权重相乘之后,调用激活函数来确定神经元是否被激活。激活函数有三种主要类型:RELU函数,sigmoid函数和双曲正切函数。我们已经熟悉了sigmoid函数。RELU函数是一个简洁的函数,它接受输入x并输出相同的数字,如果它大于0; 但是,如果输入小于0,则它等于0。双曲正切函数与sigmoid函数基本相同,只是它约束-1和1之间的任何值。

我们需要掌握的数学知识:我们在概念方面已经讨论了很多!如果你想对这里提出的数学有基本的了解,那么离散数学课程和线性代数课程是很好的起点。为了深入理解,我会推荐图论,矩阵论,多元微积分和实分析课程。如果您对学习线性代数基础知识感兴趣,可以开始使用我们的线性代数机器学习课程。
K-Means聚类
它是什么:K Means Clustering算法是一种无监督机器学习,用于对未标记数据进行分类,即没有定义类别或组的数据。该算法通过在数据中查找组来工作,其中组由变量k表示。然后,它迭代数据,根据提供的功能将每个数据点分配给k个组中的一个。K均值聚类依赖于整个算法中的距离概念,以将数据点“分配”到聚类。如果您不熟悉距离的概念,则它指的是两个给定项目之间的空间量。在数学中,任何描述集合中任意两个元素之间距离的函数称为距离函数或度量。这里有两种类型的指标:欧几里德指标和
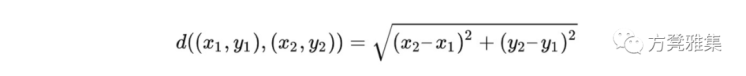
这里(x1,y1) 和 (x2,y2)是笛卡尔平面上的坐标点。虽然欧几里德度量标准已经足够,但在某些情况下它不起作用。假设你在一个大城市散步; 如果有一个巨大的建筑阻挡你的路径,说“我离目的地6.5个单位”是没有意义的。为了解决这个问题,我们可以使用
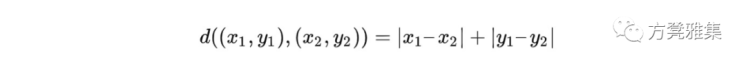
这里 (x1,y1) 和 (x2,y2) 是笛卡尔平面上的坐标点。
我们需要掌握的数学知识:这里需要的其实比较少; 实际上你只需要知道加法和减法,并理解代数的基础知识,这样你就可以掌握距离公式。但是为了深入了解每种指标存在的基本几何形状,我建议使用涵盖学习欧几里德和非欧几里德几何的几何类。为了深入理解指标和度量空间的含义,我会阅读数学分析并参加Real Analysis课程。
决策树
它是什么:决策树是一种类似流程图的树结构,它使用分支方法来说明决策的每个可能结果。树中的每个节点代表对特定变量的测试 - 每个分支都是该测试的结果。决策树依赖于一种称为信息理论的理论来确定它们是如何构建的。在信息理论中,人们对某个主题的了解越多,人们可以知道的新信息就越少。信息理论的关键措施之一被称为熵。熵是量化给定变量的不确定性量的度量。熵可以这样写:
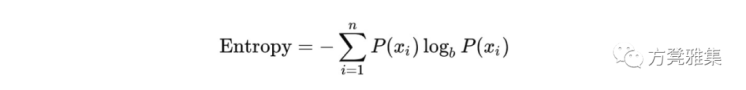
在上面的等式中, P(X)是数据集中发生特征的概率。应该注意,任何基数b都可以用于对数; 但是,常见的值是2,e(2.71)和10。您可能已经注意到看起来像“S”的花式符号。这是求和符号,它意味着可以连续添加求和之外的任何函数。添加的次数取决于求和的下限和上限。在计算熵之后,我们可以通过使用信息增益开始构造决策树,它告诉哪个分裂将最大程度地减少熵。信息获取的公式如下:
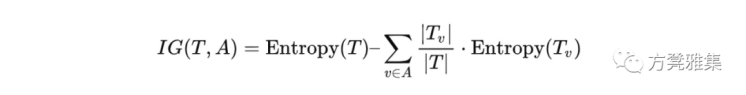
信息增益可以衡量某个人可以获得多少“信息”。在决策树的情况下,我们可以计算数据集中每个列的信息增益,以便找到哪个列将为我们提供最大的信息增益,然后在该列上进行拆分。
我们需要的数学:基本的代数和概率是你真正需要了解决策树的基础。如果你想要对概率和对数进行深入的概念性理解,我会推荐概率论和代数课程。
建议
如果你还没有参加工作,我强烈建议你学习一些纯数学和应用数学课程。你可能会畏惧他们,但是当您遇到这些算法并知道如何最好地去应用它们时,您可以学到更多有用的知识。如果您目前没有上学,我建议您前往最近的书店,阅读本文中突出显示的主题。如果您能找到涉及概率论,统计学和线性代数的书籍,我强烈建议您选择深入学习这些主题的书籍,以真正了解所描述的机器算法幕后发生的事情。