前言

昨天看到一道有意思的面试题，题目如下：

评论大致分为两种：

认为答案是 y = x + 1
认为这是一道线性回归题

仅凭直觉的话 y = x + 1 似乎符合题目要求，毕竟此函数经过其中三个点，但显然这是一个经典的使用线性回归的场景，那么我们该如何证明使用线性回归能得到比 y = x + 1 更好的结果呢？

使用库实现线性回归

我们说把大象放进冰箱只要三步，同理实现线性回归也只要三步，让我们先看看使用 scikit-learn 的线性回归模型拟合出的函数与 y = x + 1 有何不同，代码实现如下。

	
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression


def plot():
    # 重塑为 2D array 以满足模型输入要求
    x = np.array([[-1, 0, 1, 0, 1]]).reshape((-1, 1))
    y = np.array([0, 1, 1, 2, 2])

    model = LinearRegression().fit(x, y)

    plt.plot(x, model.predict(x), label=f'y = {model.coef_[0]:.3f} * x + {model.intercept_:.3f}')
    plt.plot(x, list(map(lambda a: a + 1, x)), label='y = x + 1')

    plt.scatter(x, y)
    plt.title('Simple Linear Regression')
    plt.legend()
    plt.grid()
    plt.show()


if __name__ == '__main__':
    plot()

画出来的图长下面这样，咋一看似乎很反直觉，模型给出的拟合函数距其他点的距离似乎并不比 y = x + 1 小，为啥模型会给出这个结果呢？不要着急继续往下看。

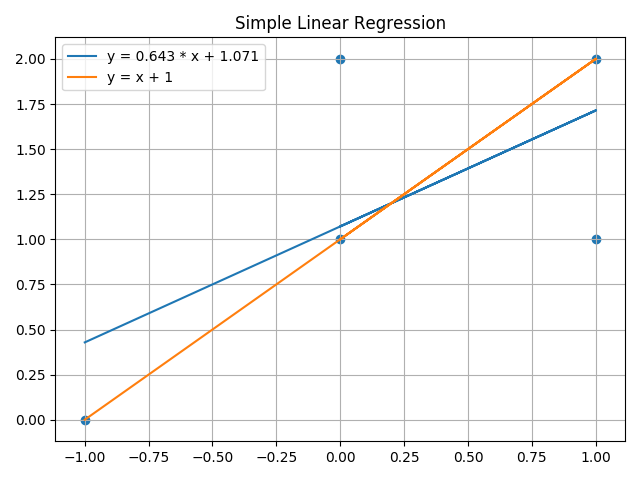
查看官方文档

对，没错，现在要做的就是了解 scikit-learn 的线性回归模型是使用何种方法实现的。打开 sklearn.linear_model.LinearRegression — scikit-learn 0.21.3 documentation 可以看到文档中赫然写着模型是用 Ordinary Least Squares 实现的（即普通最小二乘法）。

接着再往下翻一翻，可以看到模型本身提供了度量拟合优度的方法 score，使用的是决定系数（Coefficient of determination），被定义为

SS_{res} = \sum_{i=1}^n (y_i - f_i)^2
\label{eq:res}

SS_{tot} = \sum_{i=1}^n (y_i - \overline{y})^2
\label{eq:tot}

其中 $SS_{res}$ 为均方误差，与用何模型无关； $SS_{tot}$ 为模型预测结果的均方误差。因此这两个值的比例表示模型仍存在的均方误差比例， $R^2$ 表示模型消除的均方误差比例。

需要说明的是线性模型与实际值的误差是如何定义的，在此场景中无论我们使用哪个函数，其本身都可以归结为： $y = kx + b$ ，其误差为实际数据到拟合线的竖直偏移或称残差（residual），对于某点 i的残差可被计算为： $res_i = y_i - (kx + b)$ 。

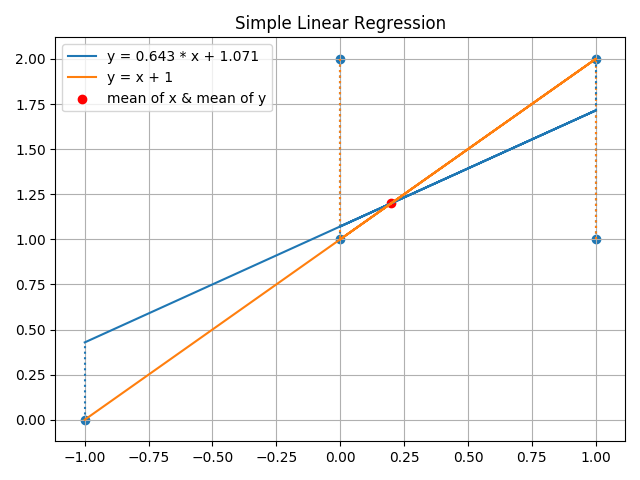
如下图所示，红点代表 x 与 y 的均值的坐标表示， $SS_{tot}$ 由数据点本身所决定。自然我们能做的是使模型预测值与实际点的残差尽可能越小越好（如图中虚线所示），我们可以使残差的绝对值最小，平方值最小，甚至立方值最小，但为什么普遍的做法是使残差平方和最小呢？主要的理由有二：

平方值和残差的正负没有关系
平方值使较大的残差具有更多的权重，但又不至于使最大的残差作用过大

故题目中求距离最短直线的方程即为求预测值与实际值残差平方和最小的方程。

仔细观察你可以发现2个函数都经过 x 与 y 的均值坐标，这一点很重要，至于为什么后文会提。

拟合优度评估

接下来我们使用决定系数评估2个函数，这里我使用 sckit-learn 自带的函数计算，当然你也可以自己实现，代码：

from sklearn.metrics import r2_score
r2_score(y_true, y_pred)

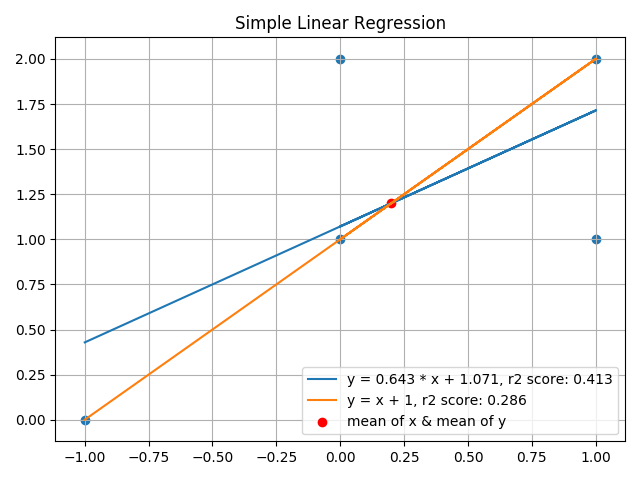
最终结果我约了3位小数，可以看到使用线性回归模型拟合的函数 $R^2$ 分数为 0.413，意味着其消除了约 41% 的误差。

OLS 推导过程

根据上文我们已经知道线性回归模型拟合的函数比 y = x + 1 更符合题意，且知道残差计算公式：

所以当线性模型的平方误差和最小时，即 $SE = \sum_{i=1}^n res_i ^ 2$ 取得最小值时，直线离其他点的距离最小。

将公式展开分析：

SE_{line} = \sum_{i=1}^n (y_i - (kx_i + b))^2 \\
= \sum_{i=1}^n(y_i^2 - 2y_i(kx_i+b) + (kx_i+b)^2) \\
= \sum_{i=1}^n(y_i^2 - 2kx_iy_i - 2by_i + k^2x_i^2 + 2kx_ib + b^2) \\
= \sum_{i=1}^n y_i^2 - 2k\sum_{i=1}^nx_iy_i - 2b\sum_{i=1}^ny_i + k^2\sum_{i=1}^nx_i^2 + 2kb\sum_{i=1}^nx_i + \sum_{i=1}^nb^2

现在上式中共有 4 个自变量，但实际上可以化简为 2 个自变量，我们知道平均数的计算为 $\overline{x} = \frac{\sum_{i=1}^n x_i}{n}$ 所以 $n\overline{x} = \sum_{i=1}^n x_i$ 。现在我们继续简化公式：

SE_{line} = \sum_{i=1}^n y_i^2 - 2k\sum_{i=1}^nx_iy_i - 2b\sum_{i=1}^ny_i + k^2\sum_{i=1}^nx_i^2 + 2kb\sum_{i=1}^nx_i + \sum_{i=1}^nb^2 \\
= n\overline{y^2} - 2nk\overline{xy} - 2nb\overline{y} + nk^2\overline{x^2} + 2nkb\overline{x} + n(b)^2

可以看到实际上线性模型的平方误差和仅取决于斜率 k 及截距 b 的取值。所以实际上是对二元函数 $SE_{line}$ 求 k , b 的一阶偏导，有：

\frac{\partial SE_{line}}{\partial k} = -2\sum_{i=1}^n x_iy_i + 2k\sum_{i=1}^nx_i^2 + 2b\sum_{i=1}^nx_i \\
= -2\sum_{i=1}^n (x_iy_i - kx_i^2 -bx_i)\\
\frac{\partial SE_{line}}{\partial b} = -2\sum_{i=1}^n y_i + 2k\sum_{i=1}^n x_i + 2\sum_{i=1}^n b \\
= -2\sum_{i=1}^n(y_i - kx_i - b)

当 $\frac{\partial SE_{line}}{\partial k} = 0$ , $\frac{\partial SE_{line}}{\partial b} = 0$ , $SE_{line}$ 取得最小值，即线性模型距此 k, b 取得最小平方误差和，有：

\begin{cases}
-2\sum_{i=1}^n(x_iy_i - kx_i^2 - bx_i) = 0\\
-2\sum_{i=1}^n(y_i - kx_i -b) = 0
\end{cases}

进而：

-2\sum_{i=1}^n(y_i - kx_i -b) = 0 \\
n\overline{y} - nk\overline{x} - nb = 0 \\
\overline{y} - k\overline{x} - b = 0

可得 $b= \overline{y} - k\overline{x}$

显然，最小二乘法得到的函数必定经过点 $(\overline{x}, \overline{y})$ ，即若要使直线距所有数据点距离最小其必定经过点 $(\overline{x}, \overline{y})$ 。

下面我们将 $\frac{\partial SE_{line}}{\partial k}$ 化简后代入 b：

-2\sum_{i=1}^n(x_iy_i - kx_i^2 - bx_i) = 0\\
\sum_{i=1}^n x_iy_i - k\sum_{i=1}^nx_i^2 - b\sum_{i=1}^n x_i = 0 \\
\sum_{i=1}^n x_iy_i - k\sum_{i=1}^nx_i^2 - (\overline{y} - k\overline{x})\sum_{i=1}^nx_i = 0 \\
\sum_{i=1}^n x_iy_i - k\sum_{i=1}^nx_i^2 - \overline{y}\sum_{i=1}^nx_i + k\overline{x}\sum_{i=1}^nx_i = 0

可得

\sum_{i=1}^nx_iy_i - \overline{y}\sum_{i=1}^nx_i = k\sum_{i=1}^n x_i^2 - k\overline{x}\sum_{i=1}^nx_i \\
k = \frac{\sum_{i=1}^n x_iy_i - \overline{y}\sum_{i=1}^n x_i}{\sum_{i=1}^n x_i^2 - \overline{x}\sum_{i=1}^n x_i} \\
k = \frac{\sum_{i=1}^n (x_i - \overline{x})(y_i - \overline{y})}{\sum_{i=1}^n (x_I - \overline{x})^2}

利用总和运算子基本性质可证 $\sum_{i=1}^n (x_i - \overline{x})(y_i - \overline{y}) = \sum_{i=1}^nx_iy_i - \overline{y}\sum_{i=1}^nx_i$

及 $\sum_{i=1}^n(x_i - \overline{x}) ^ 2 = \sum_{i=1}^nx_i^2 - \overline{x}\sum_{i=1}^nx_i$

证明如下：

\sum_{i=1}^n(x_i - \overline{x})(y_i - \overline{y}) \\
= \sum_{i=1}^n(x_iy_i - x_i\overline{y} - \overline{x}y_i + \overline{x}\overline{y}) \\
= \sum_{i=1}^nx_iy_i - n\overline{x}\overline{y} - n\overline{x}\overline{y} + n\overline{x}\overline{y} \\
= \sum_{i=1}^nx_iy_i - n\overline{x}\overline{y} \\
= \sum_{i=1}^nx_iy_i - \overline{y}\sum_{i=1}^nx_i

\sum_{i=1}^n(x_i - \overline{x}) ^ 2 \\
= \sum_{i=1}^n(x_i^2 - 2\overline{x}x_i + \overline{x}^2)\\
= \sum_{i=1}^nx_i^2 - 2n(\overline{x})^2 + n(x)^2\\
= \sum_{i=1}^nx_i^2 - n(x)^2 \\
= \sum_{i=1}^nx_i^2 - \overline{x}\sum_{i=1}^nx_i

故最后可解得普通最小二乘法公式为：

\begin{cases}
k = \frac{\sum_{i=1}^n (x_i - \overline{x})(y_i - \overline{y})}{\sum_{i=1}^n (x_I - \overline{x})^2} \\
b = \overline{y} - k\overline{x} \\
y = kx + b
\end{cases}

总结

推导出普通最小二乘法公式后我们再画出函数图线看是否与模型给出的结果一致，可见线性模型函数图线与使用普通最小二乘法得出的图线一致。

从右侧平方误差和可以看出 ols 实现的误差比 y = x + 1 要小。

代码地址点此

说说自己的心路历程吧，这题的思路就是普通最小二乘法，但一般的文章都是告诉你可以用最小二乘法实现线性回归。说实话看到给出的公式的时候我第一反应是不理解为啥，于是用一天时间一点一点找资料自己推理出公式，发现其实用到的知识就是大学高数的内容。工作忙的时候总是赶着实现，总是知其然而不知其所以然，其实静下心来了解问题背后的原理和本质反而感觉收获更多。

从一道面试题认识普通最小二乘法（Ordinary Least Squares）

前言

使用库实现线性回归

查看官方文档

拟合优度评估

OLS 推导过程

总结