十八:---删除链表的节点
18/66 题目1:在O(1)时间内出删除链表节点 给定单向链表的头指针和一个节点指针,定义一个函数在O(1)时间内删除该节点。链表节点与函数的定义如下:
struct ListNode
{
int m_nValue;
ListNode*m_pNext;
}
void DeleteNode(List**pListHead,ListNode*pToBeDelete);

在图a所示的链表中,h,i和j是三个相邻的结点。假设经过若干操作,我们已经把结点h之前的指针调整完毕,这些节点的 m_pNext 都指向前面一个节点。接下来我们把i的 m_pNext 指向h,此时的链表结构如图b所示。 (a):一个链表 (b):把i之前所有的结点的m_pNext都指向前一个结点,导致链表在结点i,j之间的断裂。 由于结点i的m_pNext指向了它的前一个结点,导致我们无法在链表中遍历到结点j。为了避免链表在结点i处断开,我们需要调整结点i的m_pNext之前,把结点j保存下来。
也就是说我们在调整结点i的m_pNext指针时,除了需要知道结点i本身之外,还需要i的前一个结点h,因为我们需要把结点i的 m_pNext指向结点h,同时,我们还事先需要保存i的一个结点j,以防止链表断开。因此相应地我们需要定义3个指针,分别指向当前遍历到的结点,它的
///
十七:---打印从1到最大的n位数
17/66 题目:输入数字n,按顺序打印从1到最大的n位十进制数。比如输入3,则打印出1,2,3一直到最大的3位数999
陷阱:当没有规定n的范围时,当输入的n很大时,定义类型位int或者long long 时都会移除,也就是我们需要考虑大数问题。
题解:把问题转化数字排列的解法,递归让代码更简洁
如果我们在数字前面补0,就会发现n位所有十进制数其实就是n个从0到9的全排列。也就是说我们把数字的每一位都从0到9排列一遍,就得到了所有的十进制数。只是在打印的时候,排在前面的0不打印出来罢了。
全排列用递归很容易表达,数字的每一位都可能是0-9中的一个数,然后设置下一位,递归结束的条件时我们已经设置了数字的最后一位。
void PrintToMaxOfNDigits(int n)
{
if(n<=0)
return;
char* number=new char[n+1];
number[n]='\0';
for(int i=0;i<10;++i)
{
number[0]=i+'0';
PrintToMaxOfNDigitsRecursively(number,n,0);
}
delete[]number;
}
void PrintToMaxOfNDigitsRecursively(char*number,int length,int index){
if(index == length-1)
{
PrintNumber(number);
return;
}
for(int i=0;i<10;++i)
{
number[index+1]=i+'0';
PrintToMaxOfNDigitsRecursively(number,length,index+1);
}
}
接下来考虑如何打印用字符串表示的数字。虽然库函数printf可以很方便的打印出一个字符串,但是在本题中调用printf并不是最合适的解决方案。我们可以这样想:当数字不够n位 的时候,在数字的前面补0,打印的时候这些补位的0不应该打印出来,比如输入3的时候,数字98用字符串表示为“098”,如果直接打印出098就不符合我们的阅读习惯。因此,我们定义了函数PrintNumber,在这个函数里,只有在碰到第一个非0的字符之后才开始打印,直至字符串的结尾。
void PrintNmuber(char* number)
{
bool isBeginning0=true;
int nLength=strlen(number);
for(int i=0;i<nlength;++i)
{
if(isBeginning0 && number[i] != '0')
is Beginnin0=false;
if(!isBeginning0)
{
printf("%c",number[i]);
}
}
printf("\t");
}
十六:---数值的整数次方
10/66 题目:给定一个double类型的浮点数base和int类型的整数exponent(实现函数double Power(double base ,int exponent))。求base的exponent次方。保证base和exponent不同时为0
题解:在C语言库中有一个pow函数可以用来求乘方,本体类似于要求实现pow的功能。 如果输入的指数exponent为32,则在函数PowerWithUnsignedExponent的循环中需要做31次乘法。换种思路来说:我们的目的是求出一个数字的32次方,如果我们已经知道了它的16次方,那么只要在16次方的基础上再平方一次就可以了。而16次方是8次方的平方,这样以此类推,我们求32次方只需要做5次乘法:先求平方,在平方的基础上再求4次方,在四次方的基础上求8次方,在8次方的基础上求16次方,最后在16次方的基础上求32次方。
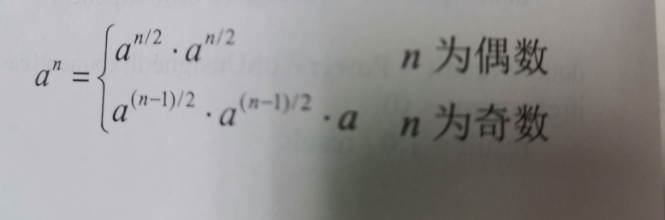
double PowerWithUnsignedExpontent(double base,unsigned int exponent)
{
if(exponent == 0)
return 1;
if(exponent == 1)
return base;
double result = PowerWithUnsignedExponent(base,exponent>>1);
result *=result;
if(exponent & 0x1 == 1)
result *= base;
return resul;
}
小细节:我们用右移运算符代替了除以2,用位与运算符代替了求余运算符(%)来判断一个数时奇数还是偶数。位运算的效率比乘数法及求余运算的效率要高很多。
对细节一定要重视:
a:判断base是否等于0
b:用位运算代替乘除法及求余运算
function Power(x,n){
if(n < 0) {
if(x <= 0) {
throw new Error("分母不能小于等于0");
}else {
if(-n % 2 == 1) {
return 1/(Power(x,-n-1) * x);
}else {
var r = 1/Power(x,-n/2);
return r * r;
}
}
}
if(n == 0) {
return 1;
}
else {
if(n % 2 == 1) {
return Power(x,n-1) * x;
}else {
var r = Power(x,n/2);
return r * r;
}
}
}
测试用例:
将底数和指数分别设为正数、负数和0;
十五:---位运算
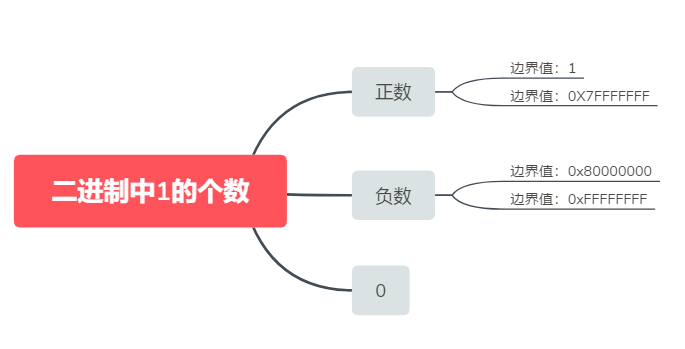
15/66 题目:请实现一个函数,输入一个整数,输出该数二进制表示中1的个数。其中负数用补码表示。例如,把9表示成二进制是1001,有两位是1,因此如果输入9,则该函数输出2
与,或,异的运算规律
与(&):有0为0,全1为1
或(|):有1为1,全0为0
异或(^):相异为1,相同为0
题解:我们先来分析把一个数减去1的情况。如果一个整数不等于0,那么该整数的二进制表示中至少有一位是1.先假设这个数的最右边一位是1,那么减去1时,最后一位变成0而其他所有位都保持不变。也就是最后一位相当于做了取反操作,由1变成了0.
接下来假设最后一位不是1而是0的情况,如果该整数的二进制表示中最右边的1位于第m位,那么减去1时,第m位由1变成0,而第m位之后的所有0变成,整数中的第m位之前的所有位都保持不变。举个例子:一个二进制数1100,它的第二位是从右边数起的一个1.减去1后第二位变成0,它后面的两位变成1,而前面的1保持不变,因此得到的结果是1011
在前面两种情况下,我们发现把一个整数减去1,都是把最右边的1变成0.如果它的右边还有0,则所有的0变成1,而它左边所有位都保持不变。接下来把一个整数和它减去1的结果做位与运算,相当于把它最右边的1变成0.还是以前面的1100为例,它减去1的结果是1011,我们把1100和1011做位与运算,得到的结果是1000,我们把1100最右边的1变成0刚好就是1000.
总结:把一个整数减去1,再和原整数做与运算,会把该整数最右边的1变成0,那么一个整数的二进制表示中有多少个1,就可以进行多少次这样的操作。基于这样的思路,写出如下代码:
int NumberOf1(int n)
{
int count =0;
while(n)
{
++count;
n = (n-1)&n;
}
return count;
}
function NumberOf1(n)
{
// write code here
var count = 0,flag=1;
while(flag){
if(n&flag)count++;
flag=flag<<1;
}
return count;
}
测试用例:
十四:剪绳子
14/66 题目:给你一根长度为n的绳子,请把绳子剪成m段(m、n都是整数,n>1并且m>1),每段绳子的长度记为k[0],k[1],...,k[m]。请问k[0]xk[1]x...xk[m]可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
题解:我们有两种不同的方法去解决这个问题。先用常规的需要O(n*n)事件和O(n)空间的动态规划的思路,接着只需要用O(1)时间和空间的贪婪算法来解决这个问题
动态规划
首先定义函数f(n)为把长度为n的绳子剪成若干段后各段长度乘积的最大值。在剪第一刀的时候,我们有n-1种可能的选择,也就是剪出来的第一段绳子的可能长度分别为1,2,...,n-1。因此f(n)=maxf(i)*f(n-i),其中0<i<n.
这是一个从上至下的递归公式由于递归会有很多重复的子问题,从而有大量的不必要的重复运算(从前有座山,山里有座庙,庙里有个老和尚在给小和尚讲故事,讲的是(从前有座山,山里有座庙,庙里有个老和尚在给小和尚讲故事,讲的是(从前有座山,山里有座庙,庙里有个老和尚在给小和尚讲故事,讲的是(...))))
我们可以用自下而上的顺序计算,也就是说我们先得到f(2)再得到f(3)....
当绳子的长度为 2时,只可能剪成长度都为1的两段,因此f(2)等于1.当绳子的长度为3时,可能把绳子剪成长度分别为1和2的两段或者长度都为1的三段,由于1x2>1x1x1,因此f(3)=2.
代码复现:
int maxProductAfterCutting_solution(int length)
{
if(length<2)
return 0;
if(length == 2)
return 1;
if(length == 3)
return 2;
}
int* products = new int[length + 1];
products[0] = 0;
products[1] = 1;
products[2] = 2;
products[3] = 3;
int max = 0;
for(int i =4;i<length;++i)
{
max=0;
for(int j = 1;j<=i/2;++i)
{
int product = products[j] * products[i-j];
if(max < product)
max=product
products[i]=max;
}
}
max = products[length];
delete[]products;
return max;
代码分析:
在上述代码中,子问题的最优解存储在数组products里。数组中第i个元素表四把长度为i的绳子剪成若干段之后各段长度乘积的最大值,即f(i).第一个for循环变量是顺序递增的,这意味着计算顺序是自下而上的。对于每一个j(0<i<j)而言,f(i)都可以求解出来,且将结果保存在projects[j]中。第二个for循环的功能是为了求出所有可能的f(j)xf(i-j),并比较出他们的最大值。
贪婪算法
如果按照如下的策略来剪绳子,则得到各段绳子的长度的乘机将最大:当n>=5时,我们尽可能多的剪长度为3的绳子;当剩下的绳子长度为4时,把绳子剪成两段长度为2的绳子。
代码参考如下:
int maxProductAfterCutting_solution2(int length)
{
if(length<2)
return 0;
if(length == 2)
return 1;
if(length == 3)
return 2;
//尽可能多的减去长度为3的绳子
int timesOf3 = length/3;
//当绳子最后剩下的长度为4的时候,不能再减去长度为3的绳子段。
//此时更好的方法是将绳子剪成长度为2的两段
if(length - timesOf * 3 ==1)
timesOf3 = 1;
int timesOf2 = (length - timeOd3 * 3)/2;
return(int)(pow(3,timesOf3))*(int)(pow(2,timesOf2));
}
接下来我们要证明这种思路的正确性:首先,当n>=5的时候,我们可以证明2(n-2)
n,并且3(n-3)>n.也就是说当绳子剩下的长度大于或者等于5的时候,我们就把他剪成长度为3或者2的绳子段,另外当n>=5时,3(n-3)>=2(n-2),因此我们应该尽可能地多剪长度为3的绳子段。
代码实现:
function cutRope(number) {
// write code here
if (number <= 2) {
return 1
}
if (number === 3) {
return 2
}
let x = Math.floor(number / 3)
let y = number % 3
if (y === 0) {
return Math.pow(3, x)
} else if (y === 1) {
return 2 * 2 * Math.pow(3, x - 1)
} else {
return 2 * Math.pow(3, x)
}
}
十三:机器人的运动范围
13/66 题目:地上有一个m行和n列的方格。一个机器人从坐标0,0的格子开始移动,每一次只能向左,右,上,下四个方向移动一格,但是不能进入行坐标和列坐标的数位之和大于k的格子。 例如,当k为18时,机器人能够进入方格(35,37),因为3+5+3+7 = 18。但是,它不能进入方格(35,38),因为3+5+3+8 = 19。请问该机器人能够达到多少个格子?
题解:当机器人从坐标(0,0)开始移动。当它准备进入坐标为(i,j)的格子时,通过检查坐标的数位和判断机器人是否能够进入。如果机器人能够进入坐标为(i.j)的格子,则再判断它能否进入4个相邻的格子(i,j-1),(i-1,j),(i,j+i),(i+1,j,)。因此,我们可以用如下的代码来实现回溯算法:
代码实现:
int movingCount(int threshold,int rows,int cols)
{
if(threshold<0||rows <=0||cols<=0)
return 0;
bool *visited = new bool[rows * cols];
for(int i=0;i<rows * cols;++i)
visited[i] = false;
int count = movingCountCore(threshold,rows,cols,0,0,visited);
delete[] visited;
return count;
}
int movingCountCore(int threshold,int rows,int cols,int row,int col,bool* visited)
{
int count = 0;
if(check(threshold,rows,cols,row,col,visited))
{
visited[row * cols + col] =true;
count = 1+movingCountCore(threshold,rows,cols,row-1,col,visited)+movingCountCore(threshold,rows,cols,row,col-1,visited)+movingCountCore(threshold,rows,cols,row+1,col,visited)+movingCountCore(threshold,rows,cols,row,col+1,visited)
}
return count;
}
下面的函数check用来判断机器人能否进入坐标为(row)的方格,而函数getDigitSum用来得到一个数字的数位之和
bool check(int threshold,int rows,int cols,int row,int col,bool* visited)
{
if(row >=0&&row <rows&&col>=0&&col<cols&&getDigitSum(row)+getDigitSum(col)<=threshold &&!visited[row* cols +col])
return false;
}
int getDigitSum(int number)
{
int sum = 0;
while(number>0)
{
sum+=number%10;
number /= 10;
}
return sum;
}
代码实现:
function movingCount(threshold, rows, cols) {
var visited = [];
for (var i = 0; i < rows; i++) {
visited.push([]);
for (var j = 0; j < cols; j++) {
visited[i][j] = false;
}
}
return moveCount(threshold, rows, cols, 0, 0, visited);
}
function moveCount(threshold, rows, cols, row, col, visited) {
if (row < 0 || row == rows || col < 0 || col == cols || visited[row][col]) {
return 0;
}
var sum = 0;
var temp = row + "" + col;
for (var i = 0; i < temp.length; i++) {
sum += temp.charAt(i) / 1;
}
if (sum > threshold) {
return 0
}
visited[row][col] = true;
return 1 + moveCount(threshold, rows, cols, row, col - 1, visited) +
moveCount(threshold, rows, cols, row, col + 1, visited) +
moveCount(threshold, rows, cols, row - 1, col, visited) +
moveCount(threshold, rows, cols, row + 1, col, visited);
}
十二:矩阵中的路径
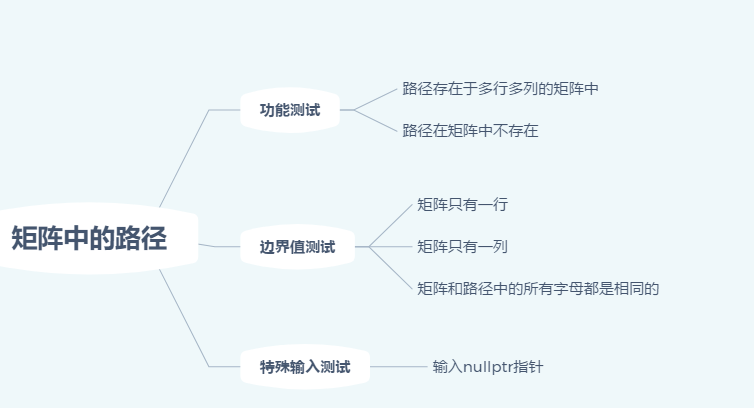
12/66 题目:请设计一个函数,用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始,每一步可以在矩阵中向左,向右,向上,向下移动一个格子。如果一条路径经过了矩阵中的某一个格子,则该路径不能再进入该格子。只能前进不能后退。
题解:
这是一个用回溯法解决的题目。首先,在矩阵中任选一个格子作为路径的起点。由于回溯法的递归特性,路径可以被看做一个栈。当在矩阵中定位了路径中前n个字符的位置之后,在与第n个字符对应的格子的周围都没有找到第n+1个字符,这时候只好在路径上回到第n-1个字符,重新定位第n个字符。
由于路径不能重复进入矩阵的格子,所以还需要定义和字符矩阵大小一样的布尔值矩阵,用来标识路径是否已经进入了这个格子。
测试用例:
代码实现:
bool hasPath(char* matrix,int rows,int cols,char* str)
{
if(matrix == nullptr || rows<1 || cols<1 || str == nullptr)
return false;
bool *visited = new bool[rows * cols]
memset(visited,0,rows * cols);
int pathLength = 0;
for(int row = 0;row<rows;++row)
{
for(int col=0;col<cols;++col)
{
if(hasPathCore(matrix,rows,cols,row,col,str,pathLength,visited)
{
return true;
}
}
}
delete[] visited;
return false;
}
bool hasPathCore(const char* matrix,int rows,int cols,int row,int col,const char* str,int& pathLength,bool* visited)
{
if(str[pathLength] == '\0')
return true
bool hasPath = false;
if(row >= 0&& row <rows&&col >= 0&&col <cols&&matrix[row * cols +col] == str[pathLength]&&!visited[row * cols +col])
{
++pathLength;
visited[row * cols +col]=true;
hasPath = hasPathCore(matrix,rows,cols,row,col-1,str,pathLength,visited)||hasPathCore(matrix,rows,cols,row-1,col,str,pathLength,visited)||hasPathCore(matrix,rows,cols,row,col+1,str,pathLength,visited)||hasPathCore(matrix,rows,cols,row+1,col,str,pathLength,visited);
if(!hasPath)
{
--pathLength;
visited[row * cols +col]=false;
}
}
return hasPath;
}
代码实现:
function hasPath(matrix, rows, cols, path)
{
if (path.length === 0) {
return true;
}
if (rows * cols < path.length) {
return false;
}
let status = [];
// 初始化status
for (let i = 0; i < rows; i++) {
status.push([]);
for(let j = 0; j < cols; j++) {
status[i][j] = false;
}
}
//找到第一个符合的path的
for (let i = 0; i < rows; i++) {
for (let j = 0; j < cols; j++) {
if (matrix[i*cols+j] === path[0]) {
if (path.length === 1) {
return true;
}
status[i][j] = true;
if (find(matrix, rows, cols, i, j, path.slice(1), status)) {
return true;
}
status[i][j] = false;
}
}
}
return false;
}
function find(matrix,rows,cols,row,col,path,status){
if(row > 0 && matrix[(row-1)*cols + col] === path[0] && status[row-1][col] === false){
if(path.length === 1){
return true;
}
status[row-1][col] = true;
if(find(matrix,rows,cols,row-1,col,path.slice(1),status)){
return true;
}
status[row-1][col] = false;
}
if(row < rows-1 && matrix[(row+1)*cols + col] === path[0] && status[row+1][col] === false){
if(path.length === 1){
return true;
}
status[row+1][col] = true;
if(find(matrix,rows,cols,row+1,col,path.slice(1),status)){
return true;
}
status[row+1][col] = false;
}
if(col > 0 && matrix[row*cols + col -1] === path[0] && status[row][col-1] === false){
if(path.length === 1){
return true;
}
status[row][col-1] = true;
if(find(matrix,rows,cols,row,col-1,path.slice(1),status)){
return true;
}
status[row][col-1] = false;
}
if(col < cols-1 && matrix[row*cols + col +1] === path[0] && status[row][col+1] === false){
if(path.length === 1){
return true;
}
status[row][col+1] = true;
if(find(matrix,rows,cols,row,col+1,path.slice(1),status)){
return true;
}
status[row][col+1] = false;
}
return false;
}
注意:当矩阵中坐标为(row,col)的格子和路径字符串中下标为pathLength的字符一样时,从4个相邻的格子(row,col-1),(row-1,col),(row,col+1),(row+1,col)中去定位路径字符串中下标为pathLength+1的字符。
如果4个相邻的格子都没有匹配字符串中下标为pathLength+1的字符,则表明当前路径字符串中下标为pathLength的字符在矩阵中的定位不正确。我们需要回到前一个字符(pathLength-1),然后重新定位。
一直重复这个过程,直到路径字符串上所有字符都在矩阵中找到合适的位置(此时str[pathLength]=='\0').
十一:旋转数组的最小数字
11/66 题目:把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。
输入一个非递减排序的数组的一个旋转,输出旋转数组的最小元素。
例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转,该数组的最小值为1。
NOTE:给出的所有元素都大于0,若数组大小为0,请返回0。
题解分析:
按照题目中旋转的规则,第一个元素应该是大于或者等于最后一个元素的(特例在后面进行分析)。
1:我们可以找到数组中间的元素。如果该中间元素位于前面的递增子数组,那么它应该大于或者等于第一个指针指向的元素。此时数组中最小的元素应该位于该中间元素的后面。我们可以把第一个指针指向该中间元素,这样可以缩小寻找的范围。移动之后的第一个指针仍然位于前面的递增子数组。
2:如果中间元素位于后面的递增子数组,那么它应该小于或者等于第二个指针指向的元素。此时该数组中最小的元素应该位于该中间元素的前面。我们可以把第二个指针指向该中间元素,移动之后的第二个指针仍然位于后面的递增子数组。
3:总结:第一个指针总是指向前面递增数组的元素,而第二个指针总是指向后面递增数组的元素。最终第一个指针将指向前面子数组的最后一个元素,而第二个指针会指向后面子数组的第一个元素。也就是说他们最终会指向两个相邻的元素,而第二个指针指向的刚好是最小的元素,这就是循环结束的条件。
测试用例
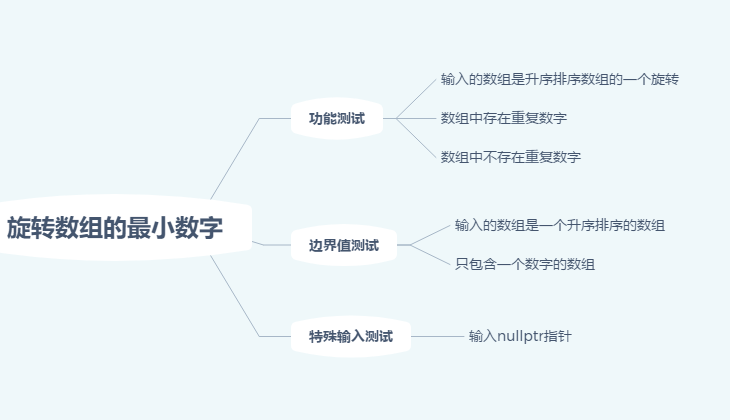
代码实现:
int Min(int* numbers,int length)
{
if(numbers = nullptr || length <= 0)
throw new std::exception("Invalid parameters");
int index1 = 0;
int index2 = length -1;
int indexMid = index1;
while(numbers[index1]>=numbers[index2])
{
if(inex2 - index1 == 1)
{
indexMid = index2;
break;
}
indexMid = (index1 + index2) /2;
if(numbers[indexMid] >= numbers[index1])
index1 = indexMid;
else if(numbers[indexMid]<=numbers[index2])
index2 = indexMid;
}
return numbers[indexMid];
}
代码实现:
while(line=readline()){
let arr = line.replace(/\[|\]/g,'').split(',');
console.log(Math.min(...arr));
}
注意:在旋转数组中由于是把递增排序数组前面的若干个数字搬到数组的后面,因此第一个数字总是大于或者等于最后一个数字。但按照定义还有一个特例:如果把排序数组的前面的0个元素搬到最后面,也就是排序数组本身,但这仍然是数组的一个旋转。此时,数组中的第一个数字就是最小的数字,可以直接返回。在上述代码中:把indexMid初始化为index1的原因。一旦发现数组中第一个数字小于最后一个数字,表明该数组是排序的,就可以直接返回第一个数字
十:斐波那契数列
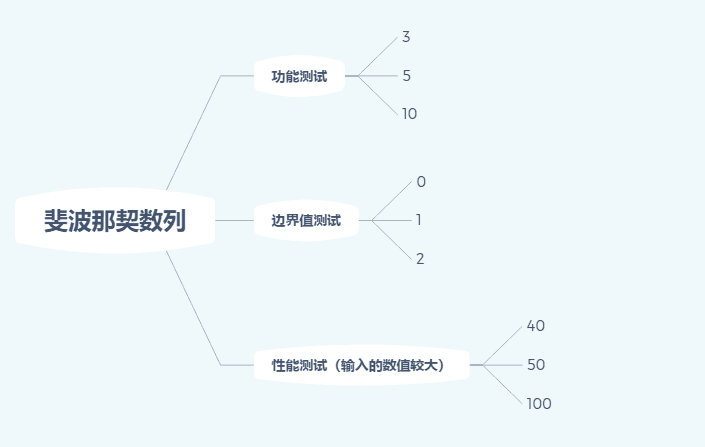
10/66 题目:大家都知道斐波那契数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项(从0开始,第0项为0)。斐波那契数列的定义如下:
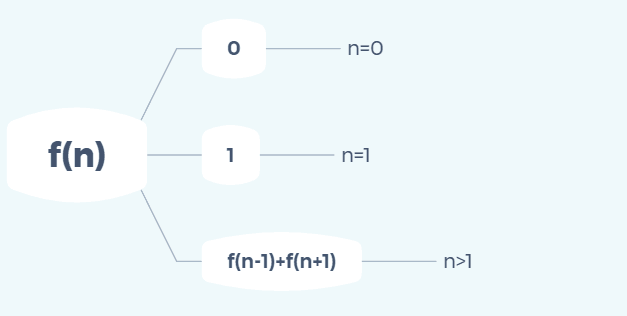
测试用例:
long long Fibonacci(unsigned n)
{
int result[2] = {0,1};
if(n<2)
return result[n];
long long fibNMinuseOne =1;
long long fibNMinuseTwo =0;
long long fibN = 0;
for(unsigned int i=2;i<=n;++i)
{
fibN = fibNMinusOne + fibNMinusTwo;
fibNMinusTwo = fibNMinusOne;
fibNMinusOne = fibN;
}
return fibN;
}
代码实现:
function Fibonacci(n)
{ if(n<=1) {return n;}
else{var f0=0;f1=1
for(var i=2;i<=n;i++){
f2=f0+f1;
f0=f1;
f1=f2;
}
return f2;}
}
九:用两个栈实现队列
关于栈和队列的基础指点参考博客:juejin.im/editor/post…
9/66 题目:用两个栈来实现一个队列,完成队列的Push和Pop操作。 列中的元素为int类型。
题解:
这道题的意图是:要求我们操作这两个 "先进后出"的栈实现一个“先进先出”的队列CQueue.
1):分别定义两个栈:栈1-stack1,栈2-stack2。当stack2不为空时,在stack2中的栈顶元素是最先进去队列的元素,可以弹出。当是stack2为空时,我们把stack1中的元素逐个弹出并压入是stack2。由于先进入队列的元素被压到stack1的底端,经过弹出和压入操作之后就处于stack2的顶端,又可以直接弹出。
2):接下来插入一个元素,我们还是把这个元素压入stack1.我们考虑下一次删除队列的头部stack2不为空,直接弹出它的栈顶元素。
测试用例:
template<typename T> void CQueue<T>::appendTail(const T& element)
{
stack.push(element);
}
template<typename T>T CQueue<T>::deleteHead()
{
if(stack2.size()<=0)
{
while(stack1.size()>0)
{
T& data = stack1.top();
stack1.pop();
stack2.push(data);
}
}
if(stack2.size( == 0)
throw new exception("queue is empty");
T head = stack2.top();
stack2.pop();
return head;
}
代码实现:
var stack1=[],stack2=[];
function push(node)
{
stack1.push(node);
}
function pop()
{
if(stack2.length==0){
if(stack1.length==0){
return null;
}else{
var len = stack1.length;
for(var i=0;i<len;i++){
stack2.push(stack1.pop());
}
return stack2.pop();
}
}else{
return stack2.pop();
}
}
同类型题型:用两个队列实现一个栈
思路:
1:根据栈的后入先出原则,最后被压入栈的应该最先被弹出。但是最后被压入队列queue1的元素位于queue1的尾部,我们每次只能从该队列的头部删除元素。因此我们可以先从queue1中删除目标元素之前的所有元素,并将删除的元素插入queue2中,再从queue1中删除目标元素。
2:当我们往栈内压入一个元素d的时候,此时queue1已经有一个元素了,我们就把该元素d插入queue1的尾部.当我们再从栈内弹出一个元素d的时候,此时被弹出的应该是最后被压入的该元素d但是因为d位于queue1的尾部,我们只能重头删除queue1的元素,并将该元素插入queue2中。
八:二叉树的下一个节点
8/66题目:给定一个二叉树和其中的一个结点,请找出中序遍历顺序的下一个结点并且返回。注意,树中的结点不仅包含左右子结点,同时包含指向父结点的指针。
解题思路:
1):如果这个节点有右子树,那么它的下一个节点就是它的右子树中的最左子节点(不要忘了,这是中序遍历序列),从右子节点出发一直沿着指向左子节点的指针,我们就能找到该节点的下一个节点。
2):如果这个节点没有右子树,且该节点为其父节点的左子节点,那么该节点的下一节点就是他的父节点。
3):如果这个节点没有右子树,且该节点为其父节点的右子节点。对于这种较为复杂的情形,我们可以沿着指向父节点的指针一直向上遍历,最终我们希望找到的是一个"它是它父节点的左子节点的节点",如果该节点存在,则该节点的父节点就是我们要找的下一个节点
测试用例:
BinaryTreeNode* GetNext(BinaryTreeNode* pNode)
{
if(pNode == nullptr)
return nullptr;
BinaryTreeNode* pNext = nullptr;
if(pNode->m_pRight != nullptr)
{
BinaryTreeNode* pRight=pNode->m_pRight;
while(pRight->m_pLeft != nullptr)
pRight = pRight->m_pLeft;
pNext = pRight;
}
else if(pNode->m_pParent !=nullptr)
{
BinaryTreeNode* pCurrent = pNode;
BinaryTreeNode* pParent = pNode->m_pParent;
while(pParent != nullptr&&pCurrent == pParent->m_pRight)
{
pCurrent = pParent;
pParent = pParent->m_pParent;
}
pNext = pParent;
}
return pNext;
}
代码实现:
/*function TreeLinkNode(x){
this.val = x;
this.left = null;
this.right = null;
this.next = null;
}*/
function GetNext(pNode)
{
if(!pNode){return null;} // 空指针
var p = null;
if(pNode.right){ // 存在右子树
p = pNode.right;
while(p.left){
p = p.left;
}
}else{ // 不存在右子树
p = pNode.next;
if(pNode.next && pNode.next.right == pNode){
while(p.next && p.next.right == p){
p = p.next;
}
if(p.next == null){
p = null;
}else{
p = p.next;
}
}
}
return p;
}
七:重建二叉树
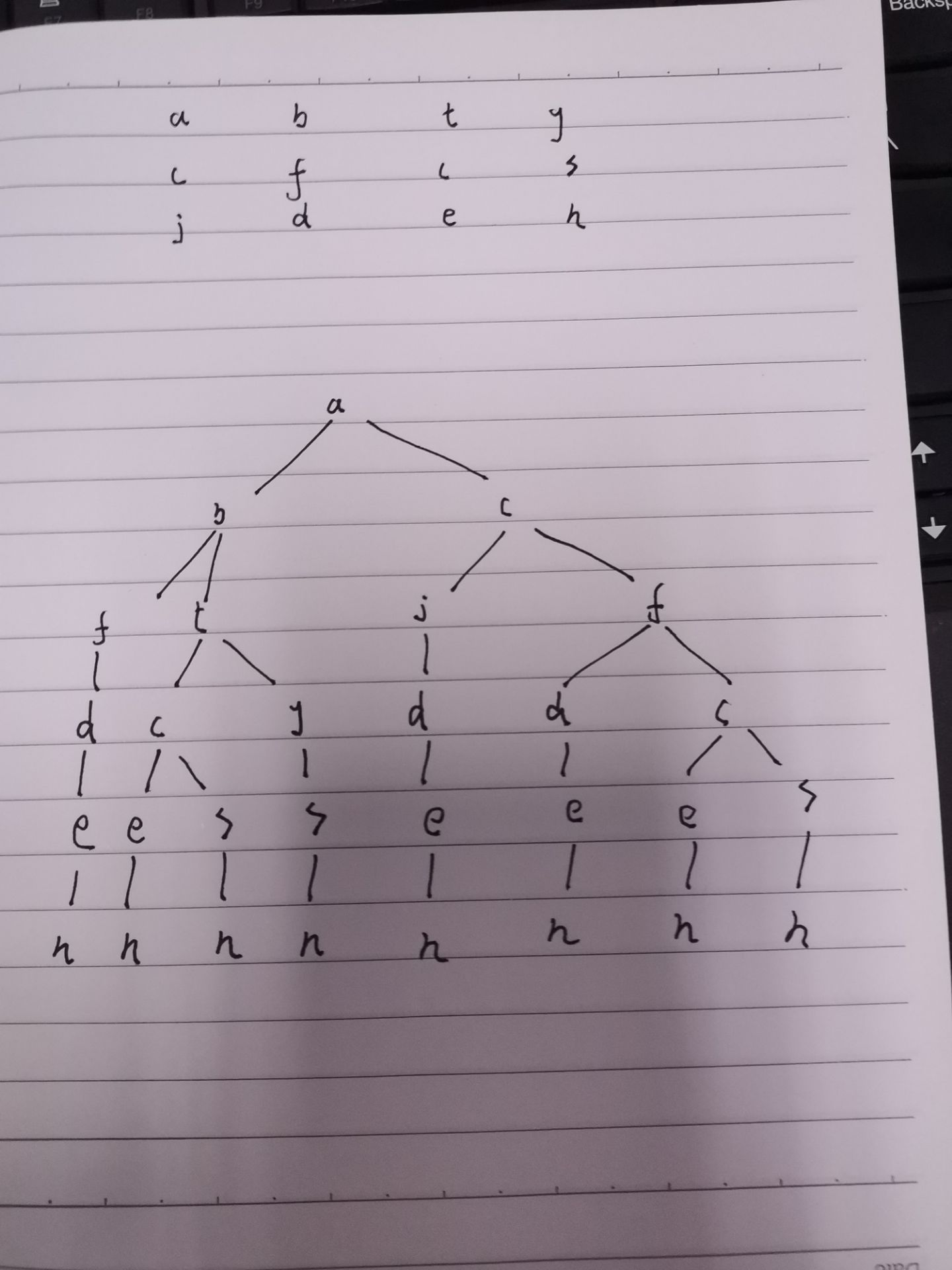
7/66 题目:输入某二叉树的前序遍历和中序遍历的结果,请重建该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如,输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历{4,7,2,1,5,3,8,6}.重建如图所示的二叉树并输出它的头节点。二叉树的节点定义如下:
struct BinaryTreeNode
{
int m_nValue;
BinaryTreeNode* m_pLeft;
BinaryTreeNode* m_pRight;
}
测试用例:
关于二叉树的介绍详见博客:juejin.cn/post/684490…
先序遍历序列:第一个节点必为根节点
中序遍历序列:根节点左边的为左子树的所有节点,根节点右边的为右子树所有的节点
我们可以先根据前序遍历序列的第一个数字确定根节点,然后再中序遍历序列中找到根节点的位置
。这样就可以确定左,右子树节点的数量。
BinaryTreeNode*Construct(int* preorder,int* inorder,int length)
{
if(preorder == nullptr||inorder == nullptr || length <= 0)
return nullptr;
return ConstructCore(preorder,preorder + length-1,inorder,inorder + length-1);
}
BinaryTreeNode* ConstructCore
(
int* startPreorder,int* endPreorder,
int* startInorder,int* endInorder
)
{
//前序遍历序列的第一个数字是根节点的值
int rootValue = startPreorder[0];
BinaryTreeNode* root = new BinaryTreeNode();
root->m_nValue=rootValue;
root->m_pLeft=root->m_pRight=nullptr;
if(startPreorder == endPreorder)
{
if(startInorder == endInorder && *startPreorder == *endPreorder )
return root;
else
throw std::exception("Invalid input.");
}
//在中序遍历序列中找到根节点的值
int* rootInorder = startInorder;
while(rootInorder<=endInorder&& *rootInorder !=rootValue)
++rootInorder;
if(rootInorder == endInorder&& *rootInorder !=rootValue)
throw std::exception("Invalid input.");
int leftLength = rootInorder - startInorder;
int* leftPreorderEnd = startPreorder + leftLength;
if(leftLength>0)
{
//构建左子树
root->m_pLeft=ConstructCore(startPreorder+1,leftPreirderEnd,startInorder,rootInorder-1);
}
if(leftLength<endPreorder-startPreorder)
{
//构建右子树
root->m_pRight=ConstructCore(leftPreorderEnd+1,endPreorder,rootInorder+1,endInorder);
}
return root;
}
代码实现:
/* function TreeNode(x) {
this.val = x;
this.left = null;
this.right = null;
} */
/*function reConstructBinaryTree(pre, vin)
{
// write code here
}*/
function reConstructBinaryTree(pre, vin)//pre:先序遍历序列;vin:中序遍历序列
{
// write code here
var result =null;
if(pre.length>1){//先序遍历不为空
var root = pre[0];//先序遍历的首字节为根节点
var vinRootIndex = vin.indexOf(root);//赋值根节点在vin中的位置
var vinLeft = vin.slice(0,vinRootIndex);//拷贝中序遍历序列0到root节点下标的数字
var vinRight = vin.slice(vinRootIndex+1,vin.length);//拷贝中序遍历序列root节点下标的数字到末尾
pre.shift();//删除先序遍历的第一个节点
var preLeft = pre.slice(0,vinLeft.length);//同理,中序遍历序列左子树拷贝到新的先序遍历中
var preRight = pre.slice(vinLeft.length,pre.length);//中序遍历序列右子树也拷贝到新的先序遍历中
result={//生成新的先序遍历序列和新的中序遍历序列
val:root,//新的根节点
left:reConstructBinaryTree(preLeft,vinLeft),//左子树
right:reConstructBinaryTree(preRight,vinRight)//右子树
}
//重复循环直到。。。
}else if(pre.length ===1){//先序遍历的长度为1
result= {
val :pre[0],//只剩下一个节点了
left:null,
right:null
}
}
return result;
}
首先需要介绍几个javascript中的方法
1:JavaScript Demo: Array.indexOf()
indexOf()方法返回在数组中可以找到一个给定元素的第一个索引,如果不存在,则返回-1。
2:Blob.slice() 方法用于创建一个包含源 Blob的指定字节范围内的数据的新 Blob 对v象。
语法:var blob = instanceOfBlob.slice([start [, end [, contentType]]]};
参数:start 可选
这个参数代表 Blob 里的下标,表示第一个会被会被拷贝进新的 Blob 的字节的起始位置。如果你传入的是一个负数,那么这个偏移量将会从数据的末尾从后到前开始计算。举例来说, -10 将会是 Blob 的倒数第十个字节。它的默认值是0, 如果你传入的start的长度大于源 Blob的长度,那么返回的将会是一个长度为0并且不包含任何数据的一个 Blob 对象。
参数:end 可选
这个参数代表的是 Blob 的一个下标,这个下标-1的对应的字节将会是被拷贝进新的Blob 的最后一个字节。如果你传入了一个负数,那么这个偏移量将会从数据的末尾从后到前开始计算。举例来说, -10 将会是 Blob 的倒数第十个字节。它的默认值就是它的原始长度(size).
参数:contentType 可选
给新的 Blob 赋予一个新的文档类型。这将会把它的 type 属性设为被传入的值。它的默认值是一个空的字符串。
3:JavaScript Demo: Array.shift()
shift() 方法从数组中删除第一个元素,并返回该元素的值。此方法更改数组的长度。
六:从头到尾打印链表
6/66 题目:输入一个链表的头节点,从头到尾反过来打印出每个节点的值。链表节点定义如下:
struct ListNode
{
int m_nKey;
ListNode* m_pNext;
};
很多人会想到把链表中链接节点的指针反转过来,改变链表的方向,然后就可以将从尾到头输出转变为从头到尾输出。
但是通常情况下,打印是一个只读操作,我们不希望打印时修改内容。
解题思路:
遍历的顺序是从头到尾,但是输出的顺序确实从尾到头。也就是说第一个遍历的反而最后一个输出,最后一个遍历的却反而第一个输出,这样的理念是典型的"后进后出",因此我们可以用栈来实现这个顺序。每经过一个节点,把该节点放到栈中。当遍历完整个链表后,再从栈顶开始逐个输出节点的值。
测试用例:
代码实现:
void PrintListReversingly_Iteratively(ListNode* pHead)
{
std::stack<ListNode*>nodes;
ListNode* pNode=pHead;
while(pHead !=nullptr)
{
nodes.push(pNode);
pNode=pNode->m_pNext;
}
while(!nodes.empty())
{
pNode=nodes.top;
printf("%d\t",pNode->m_nValue);
nodes.pop();
}
}
function printListFromTailToHead(head)
{
// write code here
var arr=[];
var me=head;
while(me){
arr.push(me.val);
me=me.next;
}
return arr.reverse();
}
但是既然可以用栈来实现这个函数,而递归的本质就是一个栈结构,于是我们可以很自然的想到用递归来实现。要实现反过来输出链表,我们每访问到一个节点的时候,先递归输出到它后面的节点,再输出该节点本身,这样链表的输出结果就反过来了
void PrintListReversingly_Recursively(ListNode* pHead)
{
if(pHead!=nullptr)
{
if(pHead->m_pNext!!=nullptr)
{
PrintListReversingly_Recursively(pHead->m_pNext);
}
printf("%d\t",pHead->m_nValue)
}
}
这种基于递归的代码虽然看起来很简洁,但是当链表非常长的时候,就会导致函数调用的层级很深, 从而有可能导致函数调用栈溢出。
五:数组中重复的数字
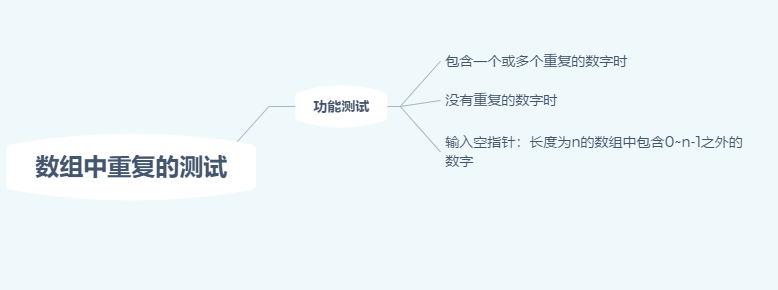
5/66 题目:在一个长度为n的数组里的所有数字都在0到n-1的范围内。 数组中某些数字是重复的,但不知道有几个数字是重复的。也不知道每个数字重复几次。请找出数组中任意一个重复的数字。 例如,如果输入长度为7的数组{2,3,1,0,2,5,3},那么对应的输出是第一个重复的数字2。
题解:现在让我们重排这个数组,从头到尾依次扫描这个数组中的每个数字。
1:当扫描到下标为i的数字时,首先比较这个数字(用m表示)是不是等于i。
2:如果是,则接着扫描下一个数字;如果不是,则再拿它和第m个数字进行比较。如果他和第m个数字相等,就找到了第一个重复的数字(该数字在下标为i和m的位置都出现了);
3:如果它和第m个数字不相等,就把第i个数字和第m个数字进行交换,把m放到属于它的位置。接下来再重复这个比较和交换的过程,知道我们发现第一个重复的数字
bool duplicate(int numbers[],int length,int* duolicate)
{
if(numbers == nullptr || length <= 0)
return false;
}
font (int i=0; i<length;++i)
{
if(numbers[i]<0 || numbers[i] >length-1)
return false;
}
for(int 1=0 ;i<length;++i)
{
while(numbers[i]!=1)
{
if(numbers[i] == numbers[numbers[i]])
{
*duplication = numbers[i];
return true;
}
int temp = numbers[i];
numbers[i]=numbers[temp];
numbers[temp]=temp;
}
}
return false;
}
在上述代码中找到的重复数字通过参数duplicate传给函数的调用者,而函数的返回值表示数组中是否有重复的数字。当数组中存在重复的数字时,返回true否则返回false
尽管这个数组中有一个两重循环,但每个数字最多只要交换两次就能找到属于自己的位置,因此总的时间复杂度时O(n),另外所有的操作步骤都是在输入数组上进行的,不需要额外分配内存,因此总的空间复杂度为O(1)
JS版代码(www.nowcoder.com/profile/893…
function duplicate(numbers, duplication)
{
// write code here
//这里要特别注意~找到任意重复的一个值并赋值到duplication[0]
//函数返回True/False
if(numbers.length==1)
return false
if(numbers==null) return false;
for(let i=0;i<numbers.length-1;i++){
for(let j=numbers.length-1;j>i;j--)
if(numbers[i]==numbers[j]){
duplication[0]=numbers[i]
return true
}
}
return false
}
重点:!!!!注意需求,还有一种需求是不改变数组且找到重复的数字(解法待更新)
四:实现Singleton模式
4/66 题目:设计一个类,我们只能生成该类的一个实例
题解:只能生成一个实例的类是实现了Singleton(单例)模式的类型。
解法有二:
其一:利用静态构造函数
C#中有一个函数能够确保只调用一次,那就是静态构造函数,利用该特性实现单例模式
public sealed class Singleton
{
private Singleton(){
}
private static Singleton instance = new Singleton();
public static Singleton Instance
{
get
{
return instance;
}
}
}
初始化静态变量instance的时候创建一个实例,由于C#在调用静态构造函数时初始化静态变量,.NET运行时能够确保只调用一个静态构造函数
当.NET运行时发现第一次使用一个类型的时候自动调用该类型的静态构造函数,因此实例instance是在第一次用到Singleton的时候就会被创建。但是。。。
注意了:假设我们在Singleton中添加一个静态方法,调用该静态函数是不需要创建一个实例的,但如果按照以上的方式实现单例模式,仍然会过早的创建实例,从而降低了内存的使用效率
我的理解:这就像将一个感应灯放在一个房子里,只要进了房子感应灯就会被触发。
其二:实现按需创建实例
public sealed class Singleton2
{
Singleton2()
{
}
public static Singleton2 Instance
{
get
{
return Nested.instance;
}
}
class Nested
{
static Nested()
{
}
internal static readonly Singleton2 instance = new Singleton2();
}
}
在上述代码中,我们在内部定义了一个私有类型Nested。当第一次用到这个嵌套类型的时候,会调用静态构造函数创建Singleton2的实例instance。类型Nested只在属性Singleton2.Instance中被用到,由于其私有属性,他人无法使用Nested类型。因此我们如果不调用属性Singleton2.Instance,就不会触发.NET运行时调用Nested,也就不会创建实例。
嗯,他的意思是把感应灯放到了房子里的盒子里,只要你不动盒子,感应灯就不会被触发
三:赋值运算符函数
3/66 题目:如下为类型CMyString的声明,请为该类型添加赋值运算符函数。
class CMystring
{
public:
CMyString(char* pData = nullptr);
CMyString(const CMyString& str);
~CMyString(void);
private:
char* m_pData;
};
解法1:
CMyString& CMyString::operator=(const CMyString &str)
{
if(this == &str)
return this;
delete []m_pData;
m_pData = nullptr;
m_pData = new char[strlen(str.m_pData)+1];
strcpy(m_pData,str.m_pData);
return *this;
}
步骤复现:
1):是否把返回值的类型声明为该类型的引用,并在函数结束前返回实例自身的引用(*this)。只有返回一个i你用,才可以允许连续赋值。否则,如果函数的返回值为void,则应用该赋值运算符将并不能进行连续赋值,假设有3个CMyString的对象:str1,str2和str3,在程序中语句str1=str2=str3将不能通过编译。
2):是否把传入的参数的类型声明为常量引用。如果传入的参数不是引用而是实例,那么从形参到实参会调用一次复制构造函数,把参数声明为引用可以避免这样的无谓消耗。同时,我们在赋值运算符函数内不会改变传入的实例的状态,因此应该为传入的引用参数加上const关键字
3)是否释放实例自身已有的内存,如果忘记在分配新内存之前释放自身已有的内存,程序将出现内存泄漏的状况。
4)判断传入的参数和当前的实例(*this)是不是同一个实例。如果是同一个,则不进行赋值操作,直接返回。如果事先不判断就进行赋值,那么在释放实例自身内存的时候就会导致:当 *this和传入的参数是同一个实例时,一旦释放了自身的内存,传入的参数的内存也同时被释放了,因为会找不到需要赋值的内容
代码升级:
CMyString&CMyString::operator=(const CMyString &str)
{
if(this != &str);
{
CMyString strTemp(str);
char* pTemp = strTemp.m_pData;
strTemp.m_pData = m_pData;
m_pData = pTemp;
}
return *this;
}
二:替换空格
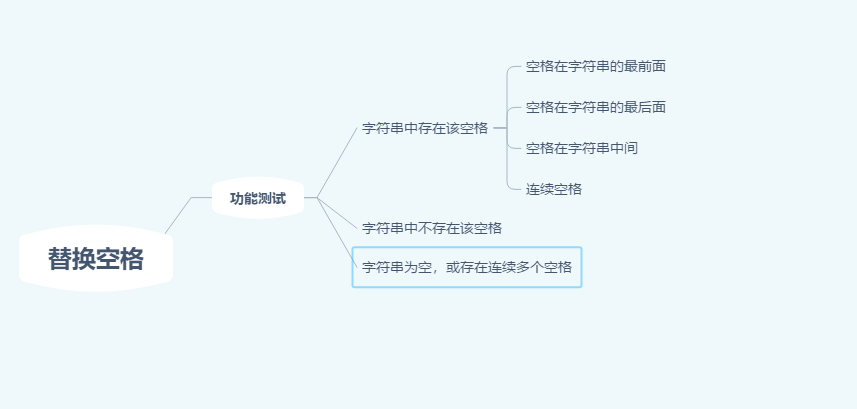
五音: 江 是霜刃出鞘亦飒然 剑花轻挽 也胜似银辉落衣衫 江湖 是我志凌云你解难 欲求胜 自当拼力一战 Aki阿杰: 千重险岭万重山 纵是风雪满 是非成败何曾惧 高处不胜寒 2/66 题目:请实现一个函数,将一个字符串中的每个空格替换成“%20”。例如,当字符串为We Are Happy.则经过替换之后的字符串为We%20Are%20Happy。
在网络编程中,如果URL参数中含有特殊字符,如空格,'#'等,则可能导致服务器端无法获得正确的参数值。我们需要将这些特殊符号转换成服务器可以识别的字符。转换的规则#'的ASCII码为35,即十六进制的0x23,它在URL中被替换成"%23"
就这道题而言,如果是在原来的字符串上进行替换,就有可能覆盖修改在该字符串后面的内存。如果是创建新的字符串并在新的字符串上进行替换,那么我们可以自己分配足够多的内存。关于这一点,面试的时候需要问清楚自己的面试官
题解:我们可以先遍历一边字符串,这样就能统计出字符串中空格的总数,并可以由此计算出替换之后的字符串的总长度。每替换一个空格,长度增加2,因此替换以后字符串的长度等于原来的长度加上2乘以空格数目
我们便以 "We are happy"为例:
思路复现:
1:把第一个指针指向字符串的末尾,把第二个指针指向替换之后的字符串的末尾。
2:依次复制字符串的内容,直至第一个指针碰到第一个空格。
3:把第一个空格替换成 "%20",把第一个指针向前移动1格,把第二个指针向前移动3格。
4:依次向前复制字符串中的字符,直至碰到空格
5:替换字符串中的倒数第二个空格,把第一个指针向前移动1格,把第二个指针向前移动3格。
测试用例:
/* length 为字符数组string的总容量*/
void ReplaceBlank(char string[],int length)
{
if(string == nullptr||length <= 0)
return;
/* originalLength为字符串string的实际长度*/
int originalLength = 0;
int numberOfBlank = 0;
int i=0;
while(string[i]!='\0')
{
++originalLength;
if(string[i] == '')
++numberOfBlank;
++i;
}
/*newLength为把空格替换成'%20'之后的长度*/
int newLength = originalLength + numberOfBlank*2;
if(newLength>length)
return;
int indexOfOriginal = originalLength;
int indexOfNew = newLength;
while(indexOfOriginal >= 0 && indexOfNew>indexOfOriginal)
{
if(string[indexOfOriginal] == '')
{
string[indexOfNew --]='0'
string[indexOfNew --]='2'
string[indexOfNew --]='%'
}
else
{
string[indexOfNew --]=string[indexOfOriginal]
}
--indexOfOriginal;
}
}
解法二:
//呵,正则表达式,不足为外人道也
function replaceSpace(str)
{
return str.replace(/\s/g,'%20')
}
一:二维数组中的查找---END
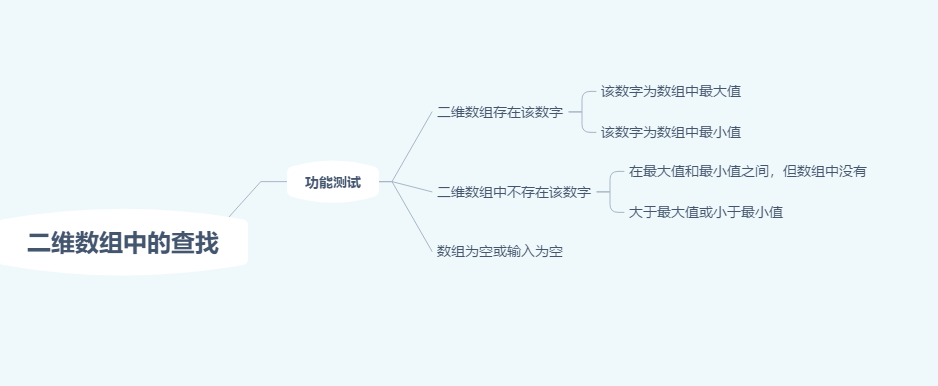
1/66 题目:在一个二维数组中(每个一维数组的长度相同),每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
题解:每行,每列都递增排序,以下图中二维数组为例,我们要查找数字7,结果应返回true,如果是查找数字5,结果应返回false
1 2 8 9
2 4 9 12
4 7 10 13
6 8 11 15
哈哈!!我懂了
我们是不是可以选择从数组的左下角或者右上角开始进行查找的?
例如:我们选择数组的右上角开始进行查找,右上角的数字为9,9>7,而9是第一列最小的那个数字所以7必然不在第四列
去掉第四列,右上角的数字就变成了8,同理,我们可以舍弃第三列
去掉第四,第三列,右上角的数字就成了2,2<7,所以7很有可能在第二列,而2是目前为止第一行最大的数,所以7并不在第一行
2 4
4 7
6 8
接下来就剩下上图所示的数组,同理因为4<7,且4>2。。。。这样就找到7了
测试用例:
那么代码怎么实现呢?
bool Find(int* matrix,int rows, int columns,int number)
{
fool found = false;
int (matrix != nullptr&&rows > 0&& columns>0)
{
int row = 0;
int column =columns - 1;
while(row<rows&&column>=0)
{
if(matrix[row * columns + column] == number)
{
found = true;
break;
}
else if(matrix[row * columns + column]>number)
-- column;
else
++ row;
}
}
return found;
}
JS代码段整理
(代码来源:www.nowcoder.com/profile/181… ):
while(line=readline()){
var index = line.indexOf(',');
var left = parseInt(line.substring(0,index));
var right = JSON.parse(line.substring(index+1));
print(Find(left,right))
}
function Find(target, array)
{
// write code here
lenX = array.length;
lenY = array[0].length;
for (var i = lenX - 1, j = 0; i >= 0 && j < lenY;) {
if (target > array[i][j]) {
j++;
}
else if (target < array[i][j]) {
i--;
}
else {
return true;
}
}
return false
}