前言
这是第一次写技术类的文章,iOS开发生涯已经是第四个年头,回头看了一下自己的学习历程,发现很多需要积累的技术性问题没有去探讨和深究。在公司的技术性研讨会上更或者是面试的时候,容易暴露自己知识点深度不够的缺点,基本上都是知其然不知其所以然,为了强迫让自己慢慢学习深究,在这里记录一下自己的学习历程及知识点,如果文章有错漏或者更好的建议,希望大家能给予指正。
RSA
为什么第一篇文章会写RSA这样的技术?因为刚好本人最近开始研究关于iOS逆向方面的资料,由此作为记录的开始。
RSA是非对称性加密算法的一种,RSA公开密钥密码体制。所谓的公开密钥密码体制就是使用不同的加密密钥与解密密钥,是一种“由已知加密密钥推导出解密密钥在计算上是不可行的”密码体制。在公开密钥密码体制中,加密密钥(即公开密钥)PK是公开信息,而解密密钥(即秘密密钥)SK是需要保密的。加密算法E和解密算法D也都是公开的。虽然解密密钥SK是由公开密钥PK决定的,由于无法计算出大数n的欧拉函数phi(N),所以不能根据PK计算出SK。正是基于这种理论,1978年出现了著名的RSA算法,它通常是先生成一对RSA密钥,其中之一是保密密钥,由用户保存;另一个为公开密钥,可对外公开,甚至可在网络服务器中注册。为提高保密强度,RSA密钥至少为500位长,一般推荐使用1024位。这就使加密的计算量很大。为减少计算量,在传送信息时,常采用传统加密方法与公开密钥加密方法相结合的方式,即信息采用改进的DES或IDEA密钥加密,然后使用RSA密钥加密对话密钥和信息摘要。对方收到信息后,用不同的密钥解密并可核对信息摘要。RSA算法是第一个能同时用于加密和数字签名的算法,也易于理解和操作。RSA是被研究得最广泛的公钥算法,从提出到现今的三十多年里,经历了各种攻击的考验,逐渐为人们接受,截止2017年被普遍认为是最优秀的公钥方案之一。其具体的数学原理我这里简单的叙述一下:
离散对数问题
求n的值,mod取模运算,3为17的原根,3和17必须为互质的整数
公式
欧拉函数ø
ø(n) 即求小于n的整数中有多少个数与n互质 如ø(8)=4 即取1,3,5,7,若n为质数,则
,求ø(n)的时候,可以对n进行因式分解,
,
,若a,b互质,则
公式
%3Dn*(1-1%2Fp))
p为质因数,如ø(8),8=,质因数只有2,
欧拉定理
公式
模反元素
当e与x互质时,一定存在一个整数d使e*d-1能被x整除,则d为e对于x的模反元素
公式即
(k为整数)
欧拉定理公式转换:
(将欧拉定理公式两边同时k次方)
(由上公式两边同时乘以m)
对比模反元素公式将代替
可得出结果
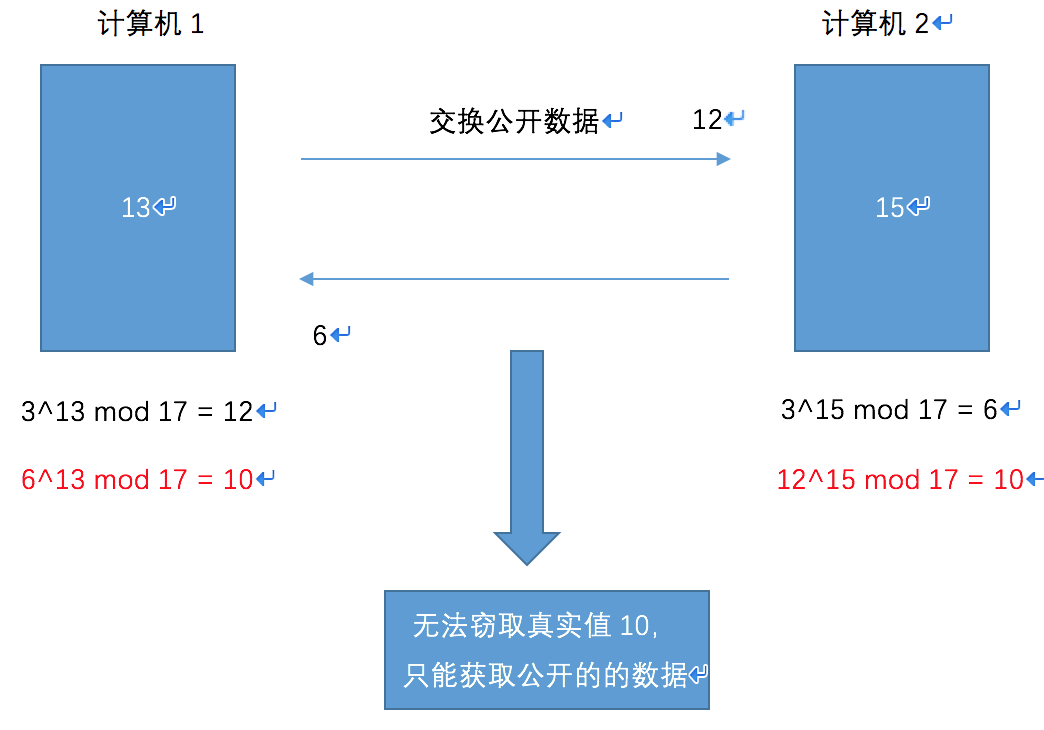
迪菲赫尔曼密钥交换
基于以上的研究迪菲和赫尔曼两人提出了在不直接传递密钥的情况下,完成密钥的交换,如图:
RSA算法
1977年三位麻省理工学院的数学家 罗纳德·李维斯特(Ron Rivest)、阿迪·萨莫尔(Adi Shamir)和伦纳德·阿德曼(Leonard Adleman)一起设计了一种算法,可以实现非对称加密。这个算法用他们三个人的名字命名,叫做RSA算法
(加密过程)
(解密过程)
其中n与e为公钥,n与d为私钥,m为明文,c为密文
除了公钥的n和e是公开的,其余的数不公开,当数据进行RSA加密后,要想破解获取明文,必须进行非常庞大的计算,因为n取的值将会非常大,至少500个二进制位,长度一般为1024位,更甚至是2048位都有,目前破除RSA必须知道知道私钥d,由于
得知,必须求出ø(n)的值,而n是一个非常大的数值,求出ø(n)非常困难,因此RSA非对称加密的安全性是比较高的
mac系统下RSA加密
因为mac系统中内置了openssl,我们可以使openssl中RSA算法的指令来操作
| 命令 | 含义 |
|---|---|
| genrsa | 生成并输入一个RSA私钥 |
| rsautl | 使用RSA密钥进行加密、解密、签名和验证等运算 |
| rsa | 处理RSA密钥的格式转换等问题 |
终端演示RSA加密
- 生成私钥

- 从私钥提取公钥

- 通过公钥加密,私钥解密


- 通过私钥签名加密,公钥解密
