引:
为了更好的呈现课堂效果,需要画一些初等函数的图形帮助学生理解
让我们从 y = sin(x)开始:
取x为-n 到 n , 每次累加一个极小值 dx 这样我们会得到连续一系列连续的点,用直线工具连接这些点,当取到足够多的点的时候连接起来,我们就会得到一条完美的sin曲线。代码大概如下:
let dx = 0.01
let points = []
for(let x = -4; x < 4; x += dx) {
points.push({
x: x,
y: Math.sin(x)
})
}
for(let n = 0; n < points.length -1; n++) {
lineTo(points[n], points[n+1])
}
problem solved! 然后,对于还有 y = kx + b 和 y = ax^2 + bx + c 或者 y = cos(x) 等,在 [-n , n] 上连续的函数,我们的方案近乎完美。 问题是否真的完美解决了呢
第一个尴尬来自于 y = 1 / x, x = 0 附近会有一条本不应该存在的连线。
分析原因不难得出,我们连接了 {-dx, -1/dx},{dx, 1/dx} 这两个点了。 这当然难不倒机智的我们,只要分别连接所有x > 0 和 x < 0的点就好了
problem solved!
画外音:让我们尝试一下 y = tan(x) 。。。
这下好了,在每一个不存在的 n * Pi/2 的点都有一条尴尬的连线。他们同样不应该存在
能不能用一种更优雅更通用的方式解决 ?
Shader思路:
通过画一个矩形,然后根据函数,控制每个像素的显示。换个说法,我们需要判断每个像素在不在函数上。该不该被画上颜色。
是不是有点像一个粉刷匠,跟粉刷匠不同的,粉刷匠是串行地涂满一面墙,这个是并行处理。
具体的思路有点类似于采样:
设y = f(x),对于任意一个像素点,我们取他周围的的八个点。把八个点的 xn,yn带入函数进行计算。两边相减,即yn - f(xn)。如果结果为正,说明点在函数上方。如果结果为负,说明点在函数下方。设想,如果这八点一半在函数上方、一半在下方是不是就可以认为这个像素就在函数上呢
OK,先上朴实无华的vertexShader
attribute vec4 a_Position;
void main() {
gl_Position = a_Position;
}
fragmentShader 核心部分
const float samples = 3.0;
int dismiss = 0;
for (float i = -1.0; i < 2.0; i += 1.0) {
for (float j = -1.0; j < 2.0; j += 1.0) {
float f = function(pos.x + i * step.x) - (pos.y + j * step.y);
count += (f > 0.) ? 1 : -1;
// 当两边相差巨大,认为是在不存在的定义域附近需要忽略掉,计算的阈值关联于你的y左边最大值
if(abs(f) > 10.0) {
dismiss += 1;
}
}
}
if(abs(count) > 5.0 || dismiss > 5) {
discard;
} else {
gl_FragColor = vec4(1.0, 0.0, 0.0, 1.0);
}
画了 y = sin(x),y = tan(x)最终效果如下
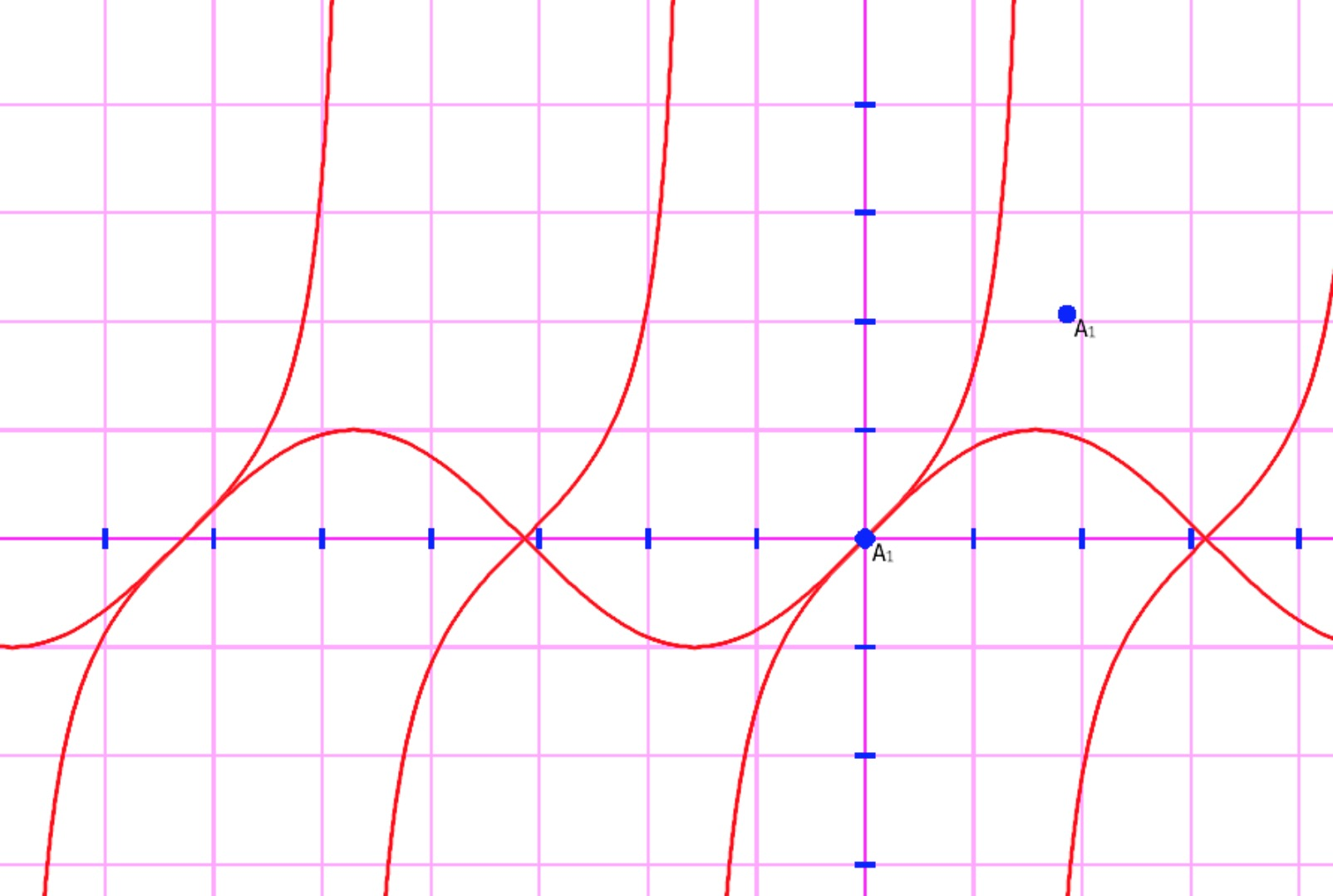
problem solved!
问题再次升级,这次我们需要画一个椭圆方程 x^2/a + y^2/b = c
幸运的是,上面的很容易扩展成左右两边的等式,具体做法,对于一般的方程式 f(x,y) = g(x,y) 这种我们只需要把之前的 y f(x)换成f(x,y) g(x,y)
涉及改动的fragment片段
float xn = pos.x + i * step.x;
float yn = pos.y + j * step.y;
float f = left(xn, yn) - right(xn, yn);
最终效果
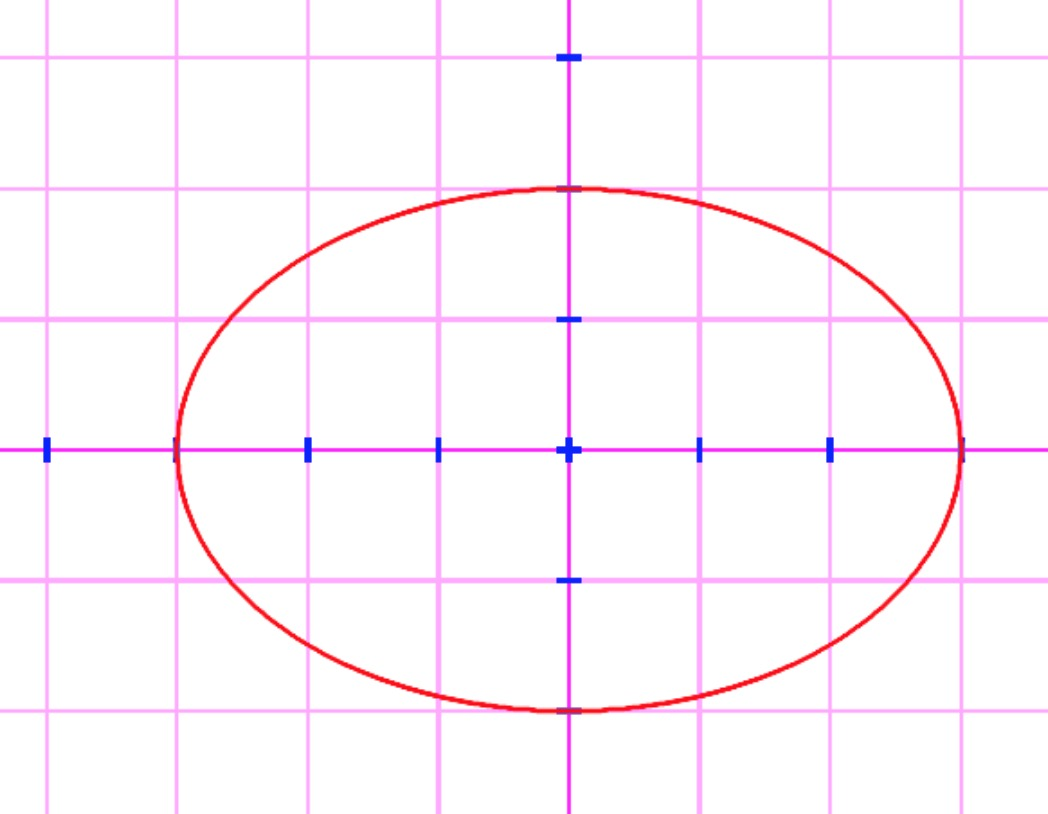
简单的边缘平滑处理
增加采样点数,对count低于某些阈值的像素做透明度处理,这里不再展开了
hope you enjoy!