前言
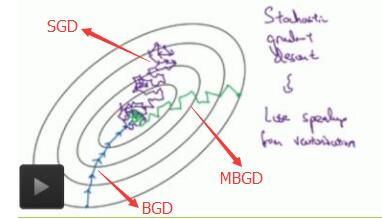
梯度下降算法是一种优化算法,机器学习中经常使用到。其主要有三类BGD(批量梯度下降算法)、SGD(随机梯度下降算法)、MBGD(小批量梯度下降算法)。最常使用到的是MBGD。
本文通过线性回归的例子进行说明,其中n代表参数个数,m代表样本个数
假设函数如下:
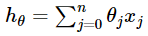
代价函数如下:
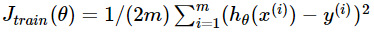
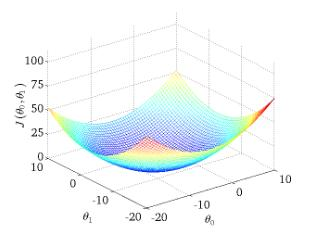
如果有theta两个参数,J的优化可以体现在三维空间中寻找最小值
一 BGD
定义:每次使用所有样本来进行更新。
相关数学计算如下:
对每个参数偏导:
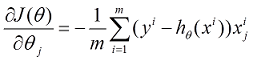
参数更新公式:
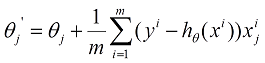
伪代码:
repeat{
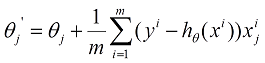
(for every j=0,1,2......n)
}
优缺点分析:
优点:
1. 迭代次数较少,准确率高,得到的是全局最优解
2. 易于并行实现
缺点:
1. 训练时间长,当样本数量很大时,速度很慢
收敛曲线:
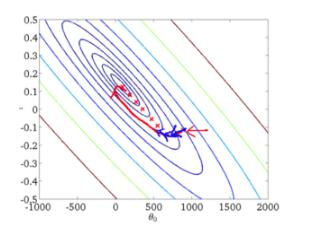
二 SGD
定义:每次更新参数使用一个样本
相关数学计算如下:
偏导和更新公式只需将BGD的m设置成1即可
伪代码:
repeat{
for(i=1,2,3......m){
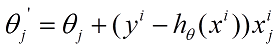
for(j=1,2,3......n)
}
}
优缺点分析:
优点:
1.训练速度快
缺点:
1.迭代次数多,得到的是局部最优解,准确率低
2.不易于并行实现
收敛曲线:
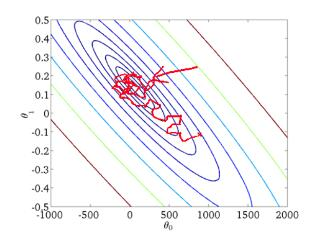
三 MBGD
定义:每次更新参数选取样本数量(batch_szie)为b个,一般b=10,假设m=1000
相关计算如下:
偏导和更新公式只需将BGD的m设置成10即可
伪代码:
repeat{
for i = 1,11......,991{
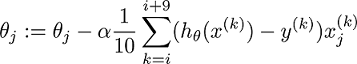
for(j=1,2,3......n)
}
}优缺点分析:
优点:
1. 既保证了准确率又保证了速度快
缺点:
2. batch_size选取不当可能会导致一些问题
四: 三种优化方法收敛曲线比较