L1Loss
也就是L1 Loss了,它有几个别称:
- L1 范数损失
- 最小绝对值偏差(LAD)
- 最小绝对值误差(LAE)
最常看到的MAE也是指L1 Loss损失函数。
它是把目标值与模型输出(估计值)
做绝对值得到的误差。
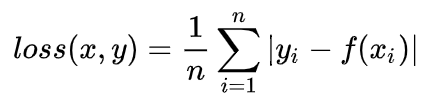
?
loss(x,y)= \frac{1}{n} \sum_{i=1}^n|y_i-f(x_i)|
?
什么时候用?
- 回归任务
- 简单的模型
- 由于神经网络通常是解决复杂问题,所以很少使用。
L2Loss
也就是L2 Loss了,它有几个别称:
- L2 范数损失
- 最小均方值偏差(LSD)
- 最小均方值误差(LSE)
最常看到的MSE也是指L2 Loss损失函数,PyTorch中也将其命名为torch.nn.MSELoss
它是把目标值与模型输出(估计值)
做差然后平方得到的误差
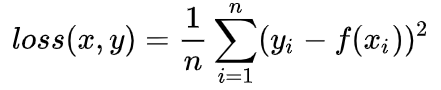
$loss(x,y)=\frac{1}{n} \sum_{i=1 }^n (y_i-f(x_i))^2$
什么时候使用?
- 回归任务
- 数值特征不大
- 问题维度不高
SmoothL1Loss
简单来说就是平滑版的L1 Loss。
原理
SoothL1Loss的函数如下:
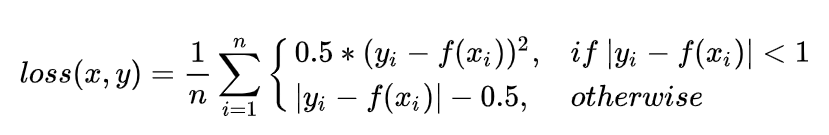
?
loss(x, y) = \frac{1}{n} \sum_{i=1}^n
\left\{
\begin{array}\\
0.5*(y_i-f(x_i))^2, & if~| y_i-f(x_i)| < 1\\
| y_i-f(x_i)| - 0.5, & otherwise
\end{array}
\right.
?
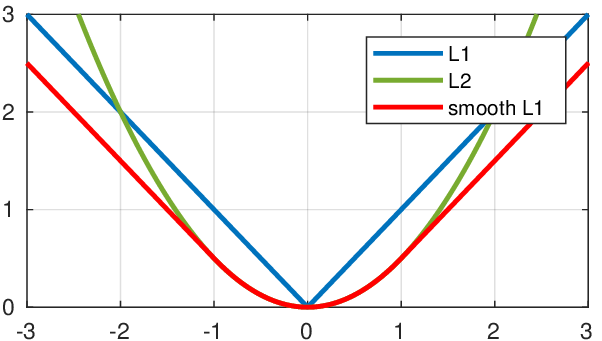
仔细观察可以看到,当预测值和ground truth差别较小的时候(绝对值差小于1),其实使用的是L2 Loss;而当差别大的时候,是L1 Loss的平移。
SooothL1Loss其实是L2Loss和L1Loss的结合,它同时拥有L2 Loss和L1 Loss的部分优点。
- 当预测值和ground truth差别较小的时候(绝对值差小于1),梯度不至于太大。(损失函数相较L1 Loss比较圆滑)
- 当差别大的时候,梯度值足够小(较稳定,不容易梯度爆炸)。
什么时候使用?
- 回归
- 当特征中有较大的数值
- 适合大多数问题
size_average=True or False
在pytorch中,所有的损失函数都带这个参数,默认设置为True。
当size_average为True的时候,计算出来的结果会对mini-batch取平均。反之,为False的时候,那算出来的绝对值不会除以n。