概念:
简单的说,递归就是方法自己调用自己,每次调用时都传入不同的变量。
递归的调用机制
1.打印问题
2.阶层问题
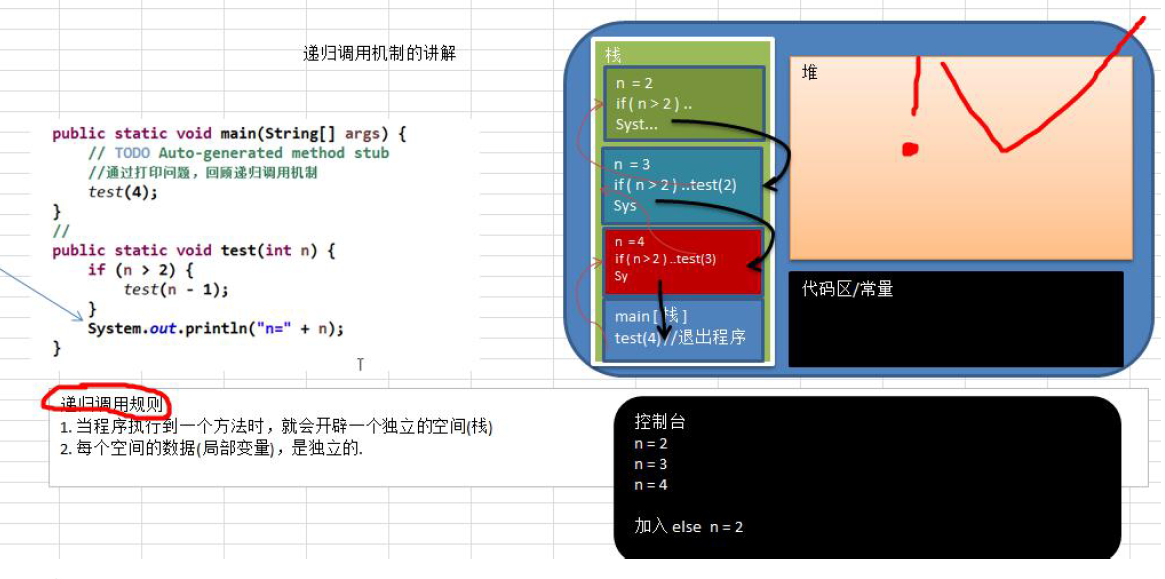
如上图,递归调用时,每次执行到方法时,就会开辟一个独立的空间(栈),依次叠加在栈顶,从上往下执行,把上一个执行的返回结果返回给下一下元素。同时每个空间的数据(局部变量)是独立的。
能够解决哪些问题
- 各种数问题,比如八皇后问题,汉诺塔,阶层问题,迷宫问题、球和篮子的问题。。。。
- 各种算法中也会用到递归。快排、归并排序、二分查找、分治算法等。。。。
- 将用栈解决的问题。
使用
三种情况常常用到递归方法。
- 定义是递归的


使用时需要注意
- 执行一个方法时就创建一个新的受保护的独立空间。
- 方法的局部变量是独立的。
- 如果方法中使用引用类型的变量(比如数组),就会共享该引用类型的数据
- 递归必须向退出递归条件逼近,否则就是会无限递归,出现栈溢出
- 当一个方法执行完毕,或遇到return,就会遵守谁调用,就将结果返回给谁。
使用递归解决迷宫问题
问题: 有一个迷宫地图,有一些可达的位置,也有一些不可达的位置(障碍、墙壁、边界)。从一个位置到下一个位置只能通过向上(或者向右、或者向下、或者向左)走一步来实现,从起点出发,如何找到一条到达终点的通路。
使用递归回溯解决八皇后问题
八皇后问题,是一个古老而著名的问题,是回溯算法的典型案例。该问题是国际西洋棋棋手马克斯·贝瑟尔于1848年提出:在8×8格的国际象棋上摆放八个皇后,使其不能互相攻击,即:任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。
斐波那契数列的函数Fib(n)的定义
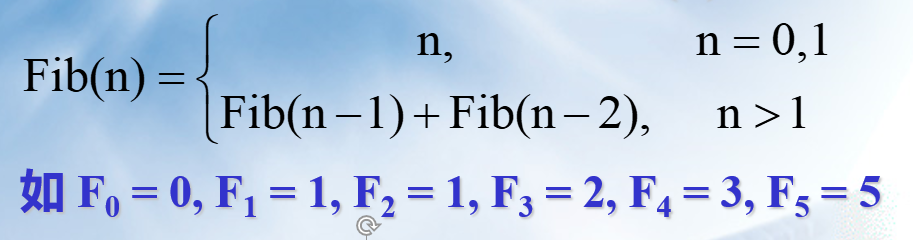
long Fib ( long n ) {
if ( n <= 1 ) return n;
else return Fib (n-1) + Fib (n-2);
}