下图是一个有向无环图
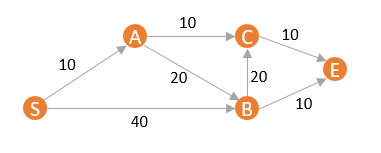
迪杰斯特拉算法是用来计算图中从某一点(例如S点)到其余各点的最短路径的一种算法,网上有很多版本的算法解释,大部分大同小异,个人认为对于一个第一次接触此算法的人来说,困惑的点往往没有说清楚,本文就简要介绍一下迪杰斯特拉算法和一些要着重理解的点。
要求:
在上面的图中寻找 S 开始到各点的最短距离。
算法思路:
1.首先将已经找到最短路径的点放入集合U中,还没找到最短路径的点放入集合P中,并且记录S到每个点的已经探索的路径中的最短距离(例如A到S的已知最短距离记为d(A))。初始化的时候,U = { S },P = { A, B, C, E},因为A和B是S的相邻节点,所以可以先找到d(A) = 10,d(B) = 40,其余的节点和S并不相邻,距离先记为无穷大,即d(C) = ∞,d(E) = ∞.
此时各节点距离分别是{ d(S) = 0,d(A) = 10,d(B) = 40,d(C) = ∞,d(E) = ∞ }。
2.在P中取出距离最小的点A,然后将其加入U集合(U = { S, A },思考为什么可以),从P中将其移除(P = { B, C, E)。
3.从P中取出的节点A有两个相邻节点B和C,那么S到B、C的距离就可能需要调整,图中 S-A-C 距离为10 + 10 = 20,而之前d(C) = ∞, 因此需要调整d(C) = 20; S-A-B的距离为10 + 20 = 30, 之前d(B) = 40,因此需要调整d(B) = 30.
此时各节点距离分别是{ d(S) = 0,d(A) = 10,d(B) = 30,d(C) = 20,d(E) = ∞ }。
重复2、3步骤,直到所有的节点都加入了U集合。
大部分的算法说明就是这些,然后就是语言的实现,然而对于初次接触的人来说,相信很多人还是一头雾水。困惑的点主要就在第2步:为什么从集合P中找到的最短距离的点,可以直接加入集合U?
证明:为什么P中距离最小的节点可以直接加入U?
下面我们就来解释这个问题。
先从S节点开始,此时P = { A, B, C, E},各节点距离分别是{ d(S) = 0,d(A) = 10,d(B) = 40,d(C) = ∞,d(E) = ∞ }。距离最小的点显然是A,那为什么就可以直接把A放到U中呢?
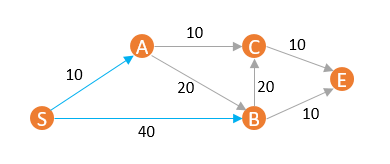
S到A要么通过S-A直达,要么通过S-B-... -A到达(图中是没有路径的,但是不妨碍我们假设),S-A为10,而S-B为40,也就是说,通过B最终到A的情况下,不论在B之后如何转接,都不可能比S-A更近了,因为光是S-B这一段就比S-A远了。所以可以认为S-A就是图中S到A的最短距离。
这里A和B均是和S直接相邻的,比较好理解,下面再来看看不是和S直接相邻的节点是怎么考虑的。
此时, P = { B, C, E},各节点距离分别是{ d(S) = 0,d(A) = 10,d(B) = 30,d(C) = 20,d(E) = ∞ },按照算法,这时候P中距离最小的节点是C,可以直接把C加入U集合中,我们再来分析一下为什么。
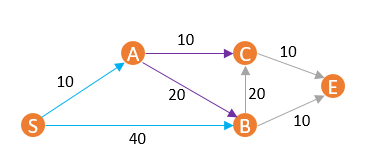
S-A-C的距离是20,而d(B) = 30, d(E) = ∞,那么,若想通过B或E(当然实际上这里E是不能到C的)
,再后续转到C节点,还有可能会比S-A-C更近吗?如果不能,那么,我们直接把C集合P中拿到集合U中就是正确的,否则就不正确。
图上看当然是不存在比S-A-C更近的路径了,但是假如图更加复杂,也就是说,疑点在于:会不会有某一个路径S-X-...-Y-C我们还没探查到,但是比S-A-C近呢?
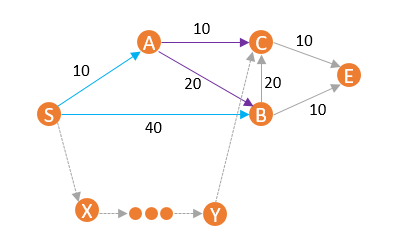
所以这里就需要证明,在逐渐向外展开探查的情况下,当从P中取出节点C时,不会有还没探索过的、到达C的、但是距离比d(C)小的路径。
采用反证法。
假设从P中取出节点C时,存在一条路径S-X-...-Y-C距离比d(C)小,但是S-X-...-Y我们还没探查到;
那么S-X-...-Y、S-X-...以及S-X的距离肯定也都比d(C)小;
而X是S的直接相邻节点,其距离是第一步就知道的,既然S-X的距离比d(C)小,那么必然会先探查X节点,这时S-X-...的距离也就知道了,既然S-X-...的距离比d(C)小,那么肯定会先探查...节点,此时S-X-...-Y的距离也有值了,既然S-X-...-Y的距离比d(C)小,也肯定比C先探查Y节点,这就和我们假设的S-X-...-Y我们还没探查到相矛盾了。
因此,得到证明。
换言之,只可能存在到C距离比d(C)大的路径还未探索,再换言之,此时的d(C)就是S到C的最短距离。
综上所述,就可以断定,直接把C从P中放到U中是正确的。
至于代码实现,网上的版本基本都是正确的,就不在赘述了。