Js算法中的树

一，树的概念

树是一种非顺序数据结构，一种分层数据的抽象模型，它对于存储需要快速查找的数据非常有用，现实生活中最常见的树的例子是家谱，或是公司的组织架构图，如下图：

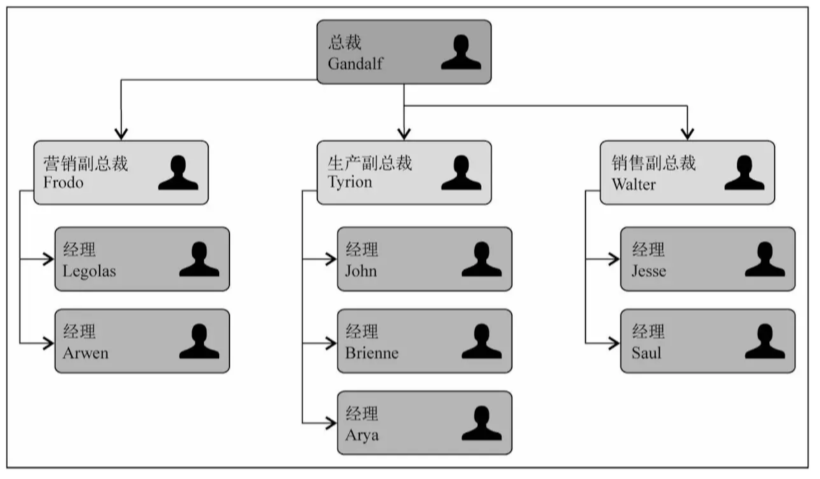
二，树的术语

• 节点的度(Degree)：节点的子树个数
• 树的度：树的所有节点中最大的度数
• 叶节点(Leaf)；度为零的节点(也成为叶子节点)
• 父节点(Parent)：有子树的节点是其子数根节点的父节点
• 子节点(Child)：若A节点是B节点的父节点，则称B节点是A节点的子节点，子节点也称孩子节点
• 兄弟节点(Subling)：具有同一父节点的个节点，彼此是兄弟节点
• 路径和路径长度：从节点n1到nk的路径为一个节点顺序n1,n2,...nk,ni是ni+1的父节点，路径所包含的个数为路径的长度
• 节点的层次(Level)：规定根节点在一层，其它任一节点的层数是父节点的层数+1
• 树的深度(Depth)：树中所有节点中最大层次是这颗树的深度

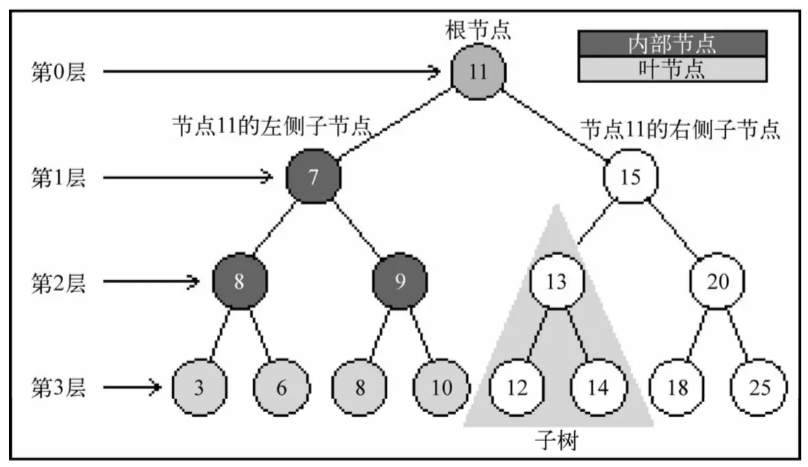
三，二叉树

1，二叉树的概念：如果树的每一个节点最多只能有两个子节点，这样的树就称为 “二叉树”，任何树都可以转换为二叉树

2，二叉树的定义

• 二叉树可以为空，也就是没有节点
• 若不为空，则它是由根节点和称其为“左子树TL”和“右子树TR”的两个不相交的二叉树组成

3，二叉树的特征

• 一个二叉树第i层最大节点数为：2^(i-1),i>=1
• 深度为k的二叉树最大节点总数为：2的K次方-1,k>=1
• 对任何非空二叉树下，若n0表示节点的个数，n2是度为2的非叶节点个数，那么两者满足关系：n0=n2+1

四，二叉搜索树

1，概念：二叉搜索树(BST,Binary Search Tree),也称为二叉搜索树

2，二叉搜索树的特性

如果树不为空

• 非空左子树的所有键值小于其根节点的键值
• 非空右子树的所有键值大于其根节点的键值
• 左，右子树本身也都是二叉搜索树

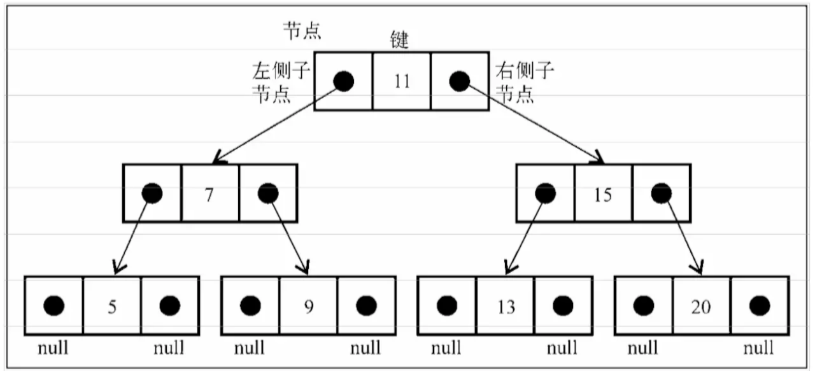
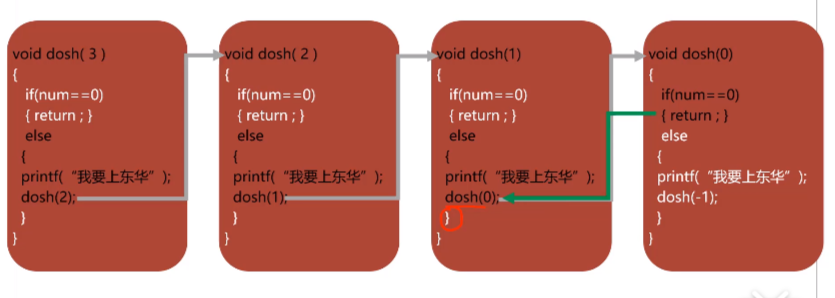
3，递归函数的原理(树的操作大部分使用递归)

void dosh(int num)
{
    if(num==0)
    {
        return ;
    }
    else
    {
        printf("我要上东华")
        dosh(num-1)
    }
}
void main()
{
    dosh(3)
}

• 实现的原理

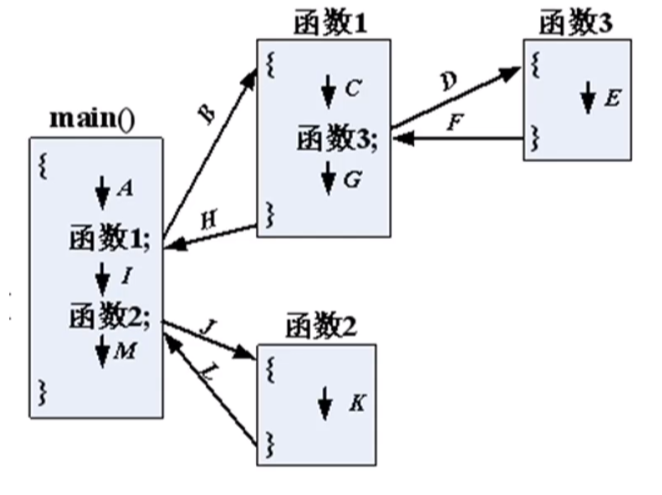
五，二叉搜索树的常见操作

• insert(key)：向树中插入一个新的键
• search(key)：向树中查找一个键，如果节点存在，则返回true，如果不存在，则返回false
• preOrderTraversal(handler)：通过先序遍历方式遍历所有的节点
• midOrderTraversal(handler)：通过中序遍历方式遍历所有的节点
• postOrderTraversal(handler)：通过后续遍历方式遍历所有的节点
• min()：返回树中最小的值
• max()：返回树中最大的值
• remove(key)：从树中移除某个键

六，二叉搜索树的实现

//定义一个节点类
class Node{
    constructor(key){
        this.key=key
        this.left=null
        this.right=null
    }
}
//封装二叉搜索树
class BinarySearchTree{
    constructor(){
        this.root=null//二叉搜索树的根
    }
    //插入操作
    insert(key){
        //根据key创建节点
        var newNode=new Node(key)
        //判断是否为第一次插入
        if(this.root==null){
            this.root=newNode
        }else{
            this.insertNode(this.root,newNode)
        }
    }
    /*
    插入的递归函数
    1,根据传入的key，创建相对应的节点
    2,向树中插入数据需要分两种情况
      第一次插入，直接修改节点即可
      第二次插入，需要进行相关的比较决定插入位置
    */
    insertNode(node,newNode){
        if(node.key>newNode.key){
            if(node.left==null){
                node.left=newNode
            }else{
                this.insertNode(node.left,newNode)
            }
        }else if(node.key<newNode.key){
            if(node.right==null){
                node.right=newNode
            }else{
                this.insertNode(node.right,newNode)
            }
        }else{//重复插入或者其它情况下不执行
            
        }
    }
    //先序遍历
    preOrderTraversal(handler){
        this.preOrderTraversalNode(this.root,handler)
    }
    //先序遍历用到的递归
    preOrderTraversalNode(node,handler){
        if(node != null){
            //1,处理经历过的节点
            handler(node.key)
            //2,查找经历过的左子节点
            this.preOrderTraversalNode(node.left,handler)
            //3,查找经历过的右子节点
            this.preOrderTraversalNode(node.right,handler)
        }
    }
    //中序遍历
    midOrderTraversal(handler){
        this.midOrderTraversalNode(this.root,handler)
    }
    //中序遍历用到的递归
    midOrderTraversalNode(node,handler){
        if(node != null){
            //1,查找经历过的左子节点
            this.midOrderTraversalNode(node.left,handler)
            //2,处理经历过的节点
            handler(node.key)
            //3,查找经历过的右子节点
            this.midOrderTraversalNode(node.right,handler)
        }
    }
    //后序遍历
    postOrderTraversal(handler){
        this.postOrderTraversalNode(this.root,handler)
    }
    //后序遍历使用到的递归
    postOrderTraversalNode(node,handler){
        if(node != null){
            //1,查找经历过的左子节点
            this.postOrderTraversalNode(node.left,handler)
            //2,查找经历过的右子节点
            this.postOrderTraversalNode(node.right,handler)
            //3,处理经历过的节点
            handler(node.key)
        }
    }
    //寻找最大值
    max(){
        var node=this.root
        var key=null
        while(node.right !=null){
            node=node.right
            key=node.key
        }
        return key
    }
    //寻找最小值
    min(){
        var node=this.root
        var key=null
        while(node.left !=null){
            node=node.left
            key=node.key
        }
        return key
    }
    //搜索key是否存在，存在返回true,否则返回false
    search(key){
        //获取根节点
        var node=this.root
        while(node !=null){
            if(node.key>key){
                node=node.left
            }else if(node.key<key){
                node=node.right
            }else{//这里表示找到了
                return true
            }
        }
        return false
    }
    /*
    删除操作
    1,找到要删除的节点，如果没有直接返回false
    2,找到了要删除的节点
       删除叶子节点
       删除只有一个子节点的节点
       删除有两个子节点的节点
    */
    remove(key){
        //1，寻找要删除的节点
        //1.1定义变量保存信息
        var current=this.root//当前的节点
        var psrent=null//父节点为null
        var isLeftChild=true//默认删除的是左节点
        //1.2,开始查找删除的节点
        while(current.key !=key){
            parent=current
            if(key<current.key){
                isLeftChild=true
                current=current.left
            }else{
                isLeftChild=false
                current=current.right
            }
            //没有找到相等的key
            if(current==null) return false
        }
        //2,找到被删除的key
        //2.1被删除的节点是叶子节点
        if(current.left==null && current.right==null){
            //也可以是根节点
            if(current==this.root){
                this.root=null
            }else if(isLeftChild){
                parent.left=null
            }else{
                parent.right=null
            }
        }
        //2.2被删除的节点只有一个子节点,isLeftChild表示这个被删除的节点是在parent的左边还是右边
        else if(current.right==null){
            //也可以是根节点
            if(current==this.root){
                this.root=current.left
            }else if(isLeftChild){
                parent.left=current.left
            }else{
                parent.right=current.left
            }
        }else if(current.left==null){
            //也可以是根节点
            if(current=this.root){
                this.root=current.right
            }else if(isLeftChild){
                parent.left=current.right
            }else{
                parent.right=current.right
            }
        }
        //删除的节点有两个子节点
        /*
        1,删除的节点有两个子节点，甚至子节点还有子节点，需要在从下面的子节点找到一个节点来替换当前的节点
        2,删除的是parent的左节点，那么需要在current的子树找一个小一点点节点来替代
        3,删除的是parent的右节点，那么需要在current的子树找一个大一点点的节点来替代
        定义：比current小一点点的节点称为current的前驱，比current大一点点的节点成为current的后继
        4,删除的节点又有两种情况：一种是删除的节点没有子孙节点，另一种是删除的节点有子孙节点
        */
        else{
            //这里是没有子孙节点的情况
            //1，获取后继节点
            var successor=this.getSuccessor(current)
            //2，判断是否为根节点
            if(current==this.root){
                this.root=successor
            }else if(isLeftChild){
                parent.left=successor
            }else{
                parent.right=successor
            }
            successor.left=current.left
        }
    }
    //找到后继点(这里用找后续的方法，也可以用前驱的方法)
    getSuccessor(delNode){
        //1,定义变量保存找到的后续
        var successor=delNode//获取后继的节点
        var current=delNode.right//当前的节点
        var successorParent=delNode//后继的父节点
        //2,循环找到后继
        while(current !=null){
            successorParent=successor//这里获取successor的父节点
            successor=current
            current=current.left//这里找最小值
        }
        //判断寻找的后继节点是否直接为delNode的right节点，这里是判断被删除的节点是否有子孙节点
        if(successor != delNode.right){
            successorParent.left=successor.right
            successor.right=delNode.right
        }
        return successor
    }
}
var bst = new BinarySearchTree()
bst.insert(11)
bst.insert(7)
bst.insert(15)
bst.insert(5)
bst.insert(3)
bst.insert(9)
bst.insert(8)
bst.insert(10)
bst.insert(13)
bst.insert(12)
bst.insert(14)
bst.insert(20)
bst.insert(18)
bst.insert(25)
console.log(bst)
var resultString_one=''
var resultString_two=''
var resultString_three=''
//测试先序遍历
bst.preOrderTraversal(function (key) {
  resultString_one += key + " "
})
console.log(resultString_one, "one")
//测试中序遍历
bst.midOrderTraversal(function (key) {
  resultString_two += key + " "
})
console.log(resultString_two, "two")
//测试后序遍历
bst.postOrderTraversal(function(key){
  resultString_three+=key+" "
})
console.log(resultString_three,"three")
console.log(bst.max(),"max")
console.log(bst.min(),"min")
console.log(bst.search(11))
//删除测试
bst.remove(9)
bst.remove(7)
bst.remove(15)
bst.remove(16)
var resultString_four = ''
//测试先序遍历
bst.preOrderTraversal(function (key) {
  resultString_four += key + " "
})
console.log(resultString_four,"four")