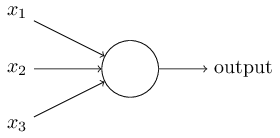
感知器(perceptron)是 人造神经元(artificial neuron)的一种,也是最基本的一种。它接受一些输入,产生一个输出。
我们在神经元里定义一些 权重(weight),经过计算之后,判断结果是否超过一个 阈值(threshold),如果超过,神经元输出 1;反之,则输出 0。
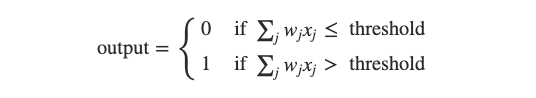
我们将变量用向量表示,并把阈值移到左边,这就得到了我们熟悉的根据权重和偏差计算的表达式:
不过这种计算方式有些缺点,当调整参数时,节点输出的值在 0 和 1 之间跃迁,也就是说,该输出是一个 阶梯函数(step function),这会对调参造成很大不便。
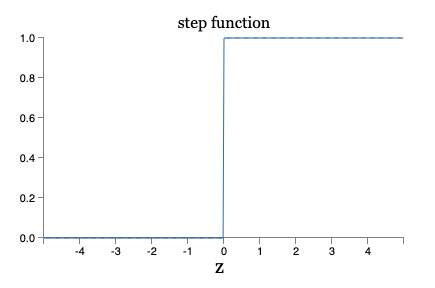
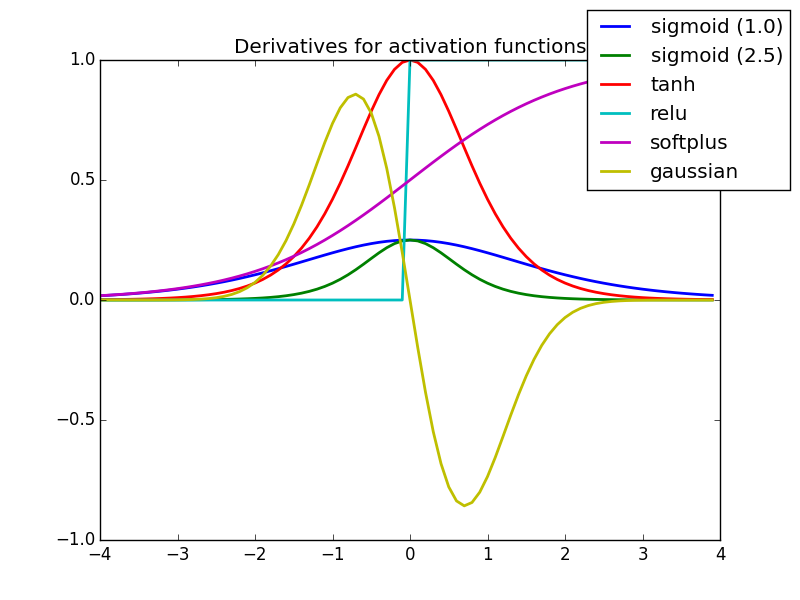
所以我们会希望输出的函数变得平滑一些,这里的函数就是 激活函数(activation functions)。
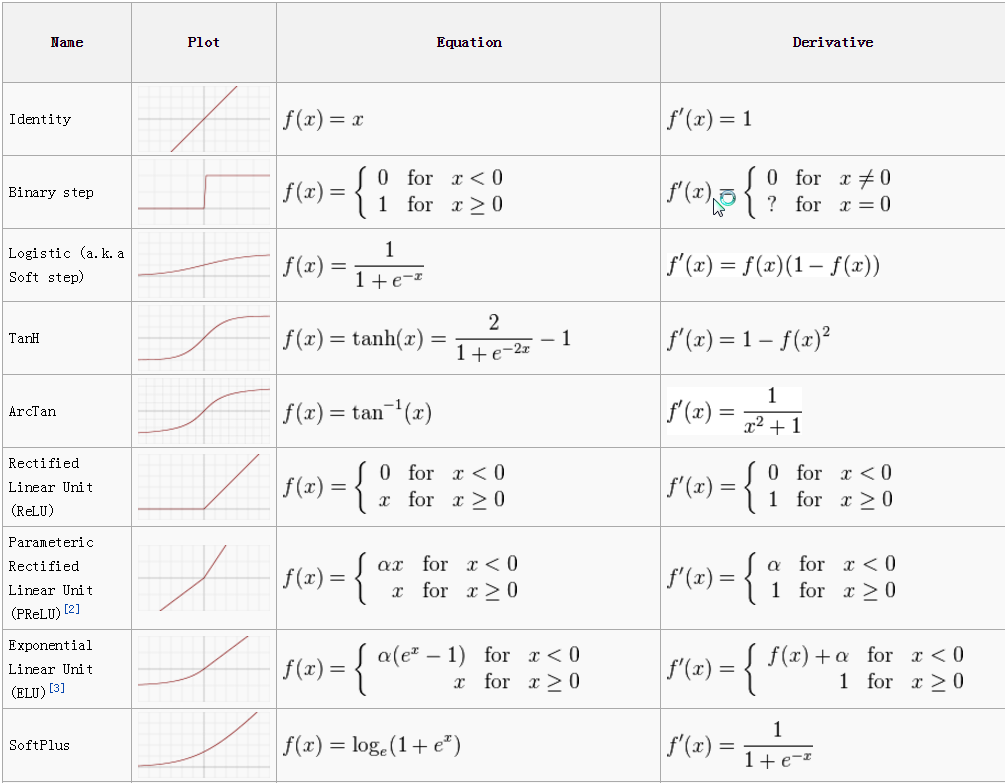
一、Sigmoid 函数
Sigmoid 函数(Sigmoid Function)又称为 Logistic 函数,是一个在生物学中常见的 S 型函数,也称为 S 型生长曲线,它将负无穷到正无穷的区间映射到了 0 到 1 中。
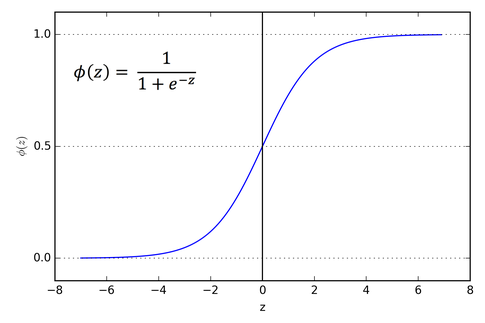
Sigmoid 函数的输入越小,输出越接近 0;输入越大输出越接近 1。除了平滑,Sigmoid 函数的另一个优点是求导非常简单,可以使用自身表示:
二、Tanh 函数
Tanh 函数(Tanh Function)是由 Sigmoid 函数推广而来,它的值域为 -1 到 1。
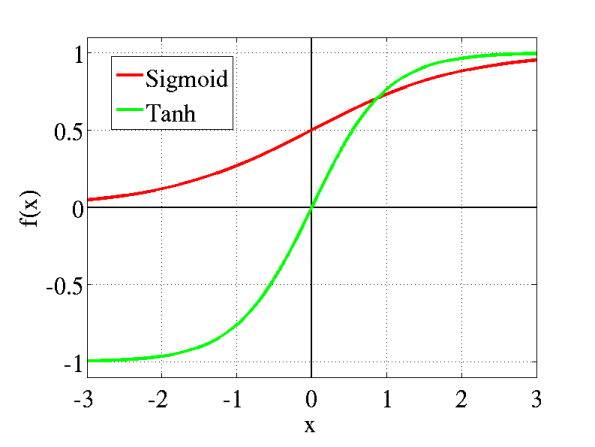
三、线性整流函数
线性整流函数(Rectified Linear Unit, ReLU),又称 修正线性单元。如果 x 为正,则输出 x,否则为 0。它的值域是 [0, inf)。
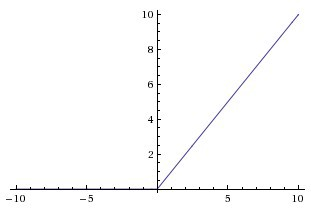
四、带泄露线性整流函数
带泄露线性整流函数(Leaky ReLU)是线性整流函数的一个变种,它的出现是为了解决 dying ReLU 问题
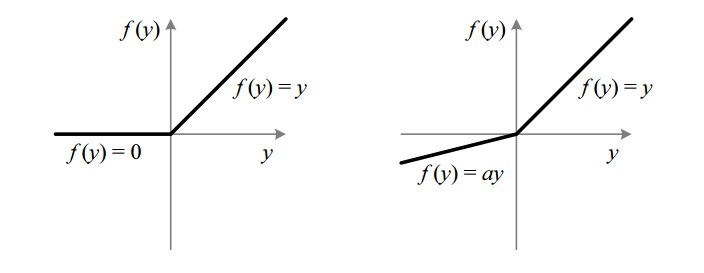
另外,当 a 不为 0.01 时,它又被称为 带泄露随机线性整流(Randomized Leaky ReLU,RReLU)。
总结
各种激活函数如下: