「动态规划」「leetcode」221.最大正方形

原题

在一个由 0 和 1 组成的二维矩阵内，找到只包含 1 的最大正方形，并返回其面积。

示例:

输入: 

1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0

输出: 4

思路

如何确定某一点为正方形的右下角的点，我们需要确定当前点的上，左，左上方向是否为1，如果同时为1, 我们则可以确定，该点可以作为一个2 x 2正方形的右下角的点。

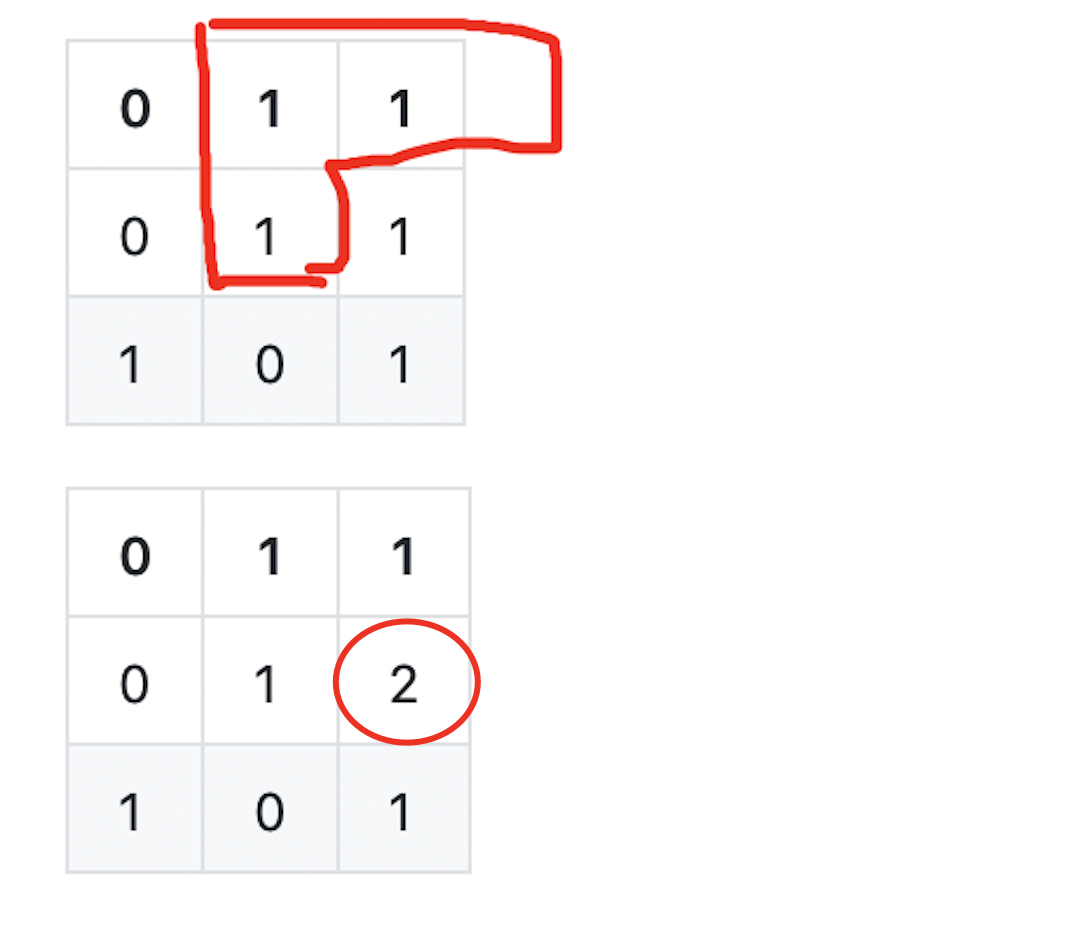
对于3 x 3的正方形，对于我们通过下图可知，正方形右下角的点的上，左，左上的三个方向，必须包含了3个2 X 2的正方形。

也就是说，对于3 X 3的正方形的右下角的点，该点上，左，左上方向上的点，必须为2。

依次类推，对于4 X 4的正方形的右下角的点，该点上，左，左上方向上的点，必须为3。如果有3个方向，有一点不满足条件，则无法成为4 x 4的正方形。

经过推导，我们可以总结出如下，状态转移方程：

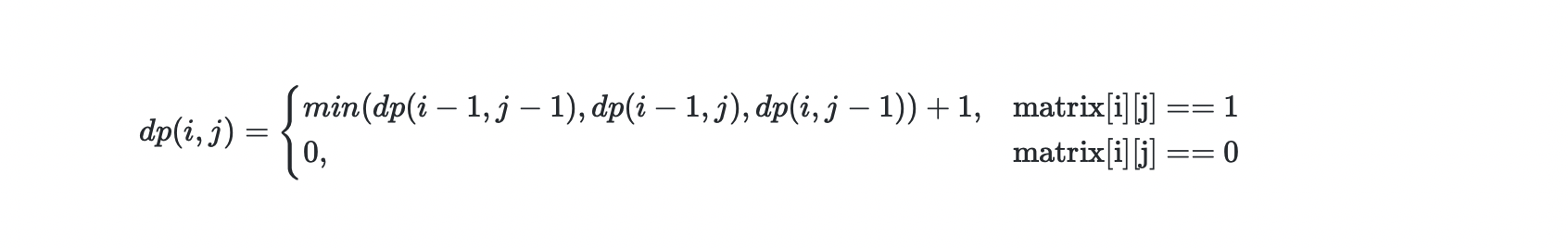
代码

/**
 * @param {character[][]} matrix
 * @return {number}
 */
var maximalSquare = function(matrix) {
    if (matrix.length === 0) {
        return 0
    }
    
    const w = matrix[0].length
    
    const h = matrix.length
    
    const dp = []
    
    let max = 0
    
    for (let i = 0; i < h; i++) {
        dp[i] = []
    }
    
    for (let i = 0; i < h; i++) {
        for (let j = 0; j < w; j++) {
            if (matrix[i][j] === '0') {
                dp[i][j] = 0
            } else {                
                const rightTop = dp[i - 1] === undefined ? 0 : dp[i - 1][j - 1] === undefined ? 0 : dp[i - 1][j - 1]
                const top = dp[i - 1] === undefined ? 0 : dp[i - 1][j]
                const right = dp[i][j - 1] === undefined ? 0 : dp[i][j - 1]
                dp[i][j] = Math.min(rightTop, top, right) + 1
            }
            
            if (dp[i][j] > max) {
                max = dp[i][j]
            } 
        }
    }
    
    return max * max
};