【论文阅读+理解】SPHERICAL CNNS
(引用框里是原文,引用框下面是解释)
1.引言
背景:近年来,在无人机、机器人和自动驾驶的全方位视觉、分子回归问题以及全球天气气候模拟等领域,对能够处理球形信号模型的需求越来越多。用普通的卷积网络对球形信号做处理注定是会失败的,因为这种投影引入的空间变化的扭曲会使权值共享失效。
在本文中,我们介绍了构建球形CNN的模块并提出了球面互相关的定义,它既具有表现力又具有旋转等变性。球面互相关满足广义傅立叶定理,所以我们能够用快速傅里叶变换(FFT)计算它。我们证明了应用于三维模型识别和雾化能量回归的球形CNN的计算效率,数值精度和有效性。
2.介绍
1INTRODUCTION
Convolutional networks are able to detect local patterns regardless of their position in the image. Like patterns in a planar image, patterns on the sphere can move around, but in this case the “move” is a 3D rotation instead of a translation. In analogy to the planar CNN, we would like to build a network that can detect patterns regardless of how they are rotated over the sphere.
传统的卷积网络可以检测到平面图片上任意位置的pattern,简单的例子,就是当目标出现在输入图片中的不同位置,输出的feature map应该是只是进行了平移变换。

对比平面的卷积,作者想搭建一个可以检测到球面任意位置patten的网络。无论目标在图像上如何旋转,这个网络都能检测到。
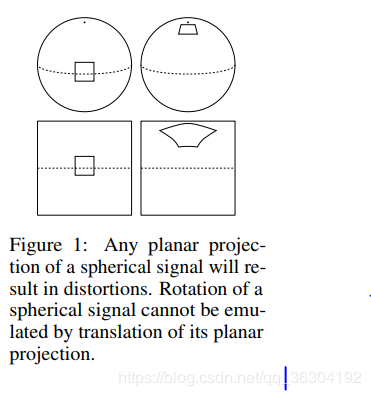
As shown in Figure 1, there is no good way to use translational convolution or cross-correlation1 to analyze spherical signals. The most obvious approach, then, is to change the definition of crosscorrelation by replacing filter translations by rotations. Doing so, we run into a subtle but important difference between the plane and the sphere: whereas the space of moves for the plane (2D translations) is itself isomorphic to the plane, the space of moves for the sphere (3D rotations) is a different, three-dimensional manifold called SO(3). It follows that the result of a spherical correlation (the output feature map) is to be considered a signal on SO(3), not a signal on the sphere, S2. For this reason, we deploy SO(3) group correlation in the higher layers of a spherical CNN.
如果用传统的卷积网络处理球面图像,如figure1,球面信号的平面投影会导致扭曲失真,所以球面信号的旋转不能通过其平面投影的平移来模拟。鉴于此,只有重新定义卷积,即改变互相关的定义,把滤波器的平移操作转变为旋转完成卷积操作。
在这里,作者引入了群论的概念。群是一种代数结构,包含一个集合和一个运算。集合里的元素在运算之后的结果仍然在集合G中,具有这种封闭性质的就是群。以三维旋转群SO(3)为例,三维旋转群SO(3)包含集合和运算,集合G内的元素是有限个3x3旋转矩阵,运算是矩阵乘法,这些旋转矩阵任意两个相乘的结果仍然是集合里的元素,表达式为(G,*)。SO(3)包含了所有绕原点的旋转。这样看来,球面绕原点的旋转是SO(3)一个元素,所以自然而然想到引入群论的概念。
The implementation of a spherical CNN (S2-CNN) involves two major challenges. Whereas a square grid of pixels has discrete translation symmetries, no perfectly symmetrical grids for the sphere exist. This means that there is no simple way to define the rotation of a spherical filter by one pixel. Instead, in order to rotate a filter we would need to perform some kind of interpolation. The other challenge is computational efficiency; SO(3) is a three-dimensional manifold, so a naive implementation of SO(3) correlation is O(n6)
实现球面CNN存在两个难题:1)如下图所示,平面图像的像素网格具有平移对称性,也就是说滤波器平移后会和图像部分区域相重合(形状大小不变),但是对于球面图像来说,没有像这样的对称网格,所以在旋转滤波器之前,需要进行插值操作,使其拥有”旋转对称性“,即滤波器旋转后会和图像部分区域重合。2)计算效率。在三维空间的计算复杂度达O(n^6)。为此,作者利用广义傅里叶变换来解决这两个问题。
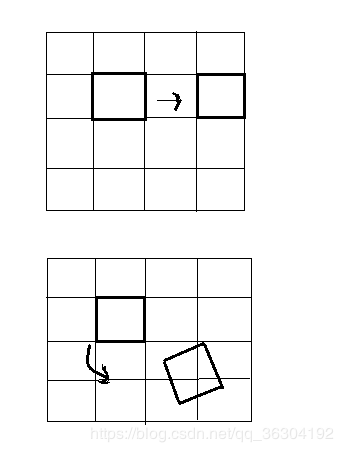
注:(示意图不要太当真)从图上可以看到,上面一幅图具有平移对称性,下面一幅图不具有旋转对称性
3.球面和旋转群上的互相关
Because the output feature map is indexed by a rotation, it is modelled as a function on SO(3). We will discuss this issue in more detail shortly.In what follows, we will go through the required concepts one by one and provide a precise definition. Our goal for this section is only to present a mathematical model of spherical CNNs. Generalized Fourier theory and implementation details will be treated later.
前面提到球面绕原点的旋转是SO(3)的一个元素,那么球面卷积输出的feature map会和这个3维的旋转有关,所以把feature map建模成SO(3)上的一个函数f(R)f(R)f(R),R是SO(3)中的一个元素,即旋转矩阵。下面对球形卷积做数学上的定义。
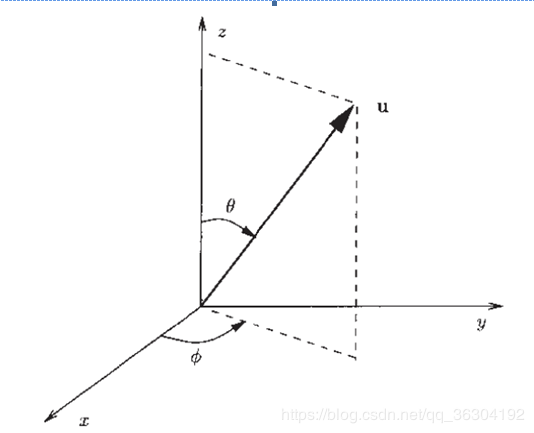
The Unit Sphere S2 can be defined as the set of points x∈R3 with norm 1. It is a two-dimensional manifold, which can be parameterized by spherical coordinates α ∈[0,2π] and β∈ [0,π] .
单位球面是R3空间所有范数为1的点的集合,可以用球面坐标参数化α ∈[0,2π] and β∈ [0,π]。下图中的ϕ
ϕ ϕ 即为α
α α ,θ
θ θ 即为β
β β 。
Spherical Signals We model spherical images and filters as continuous functions f : S2 ->RK,where K is the number of channels.
把球面图像和滤波器看成连续的函数f f f ,即fff是S2到RK空间的一个映射。
Rotations The set of rotations in three dimensions is called SO(3), the “special orthogonal group”. Rotations can be represented by 3 × 3 matrices that preserve distance (i.e. jjRxjj = jjxjj) and orientation (det® = +1). If we represent points on the sphere as 3D unit vectors x, we can perform a rotation using the matrix-vector product Rx. The rotation group SO(3) is a three-dimensional manifold, and can be parameterized by ZYZ-Euler angles α ∈ [0,2π], β ∈ [0,π], and γ ∈ [0,2π] .
三维旋转可由欧拉角α
α α , β
β β , γ
γ γ 参数化,α ∈ [0,2π], β ∈ [0,π], and γ ∈ [0,2π] .如此,三维旋转群SO(3)中的一个旋转矩阵R=Z(α
α α )Y(β
β β )Z(γ
γ γ ),其中:
Z (α) =( c osα − sinα 0 s inα c osα 0 0 0 1 ) Y( β) =( c osβ 0 s inβ 0 1 0 − sinβ 0 c osβ )
Z ⎛ ⎝⎜ α⎞ ⎠⎟ =⎛ ⎝⎜ c osα s inα 0 − sin α c osα 0 0 0 1 ⎞ ⎠⎟ Y ⎛ ⎝⎜ β ⎞ ⎠⎟ = ⎛ ⎝⎜ c os β 0 − si nβ 0 1 0 s in β 0 c os β ⎞ ⎠ ⎟ Z( α) = ⎝ ⎛ c o s α s i n α 0 − s i n α c o s α 0 0 0 1 ⎠ ⎞ Y ( β ) = ⎝ ⎛ c o s β 0 − s i n β 0
1 0 s i n β 0 c o s β ⎠ ⎞
Rotation of Spherical Signals In order to define the spherical correlation, we need to know not only how to rotate points x ∈S2 but also how to rotate filters (i.e. functions) on the sphere. To this end, we introduce the rotation operator LR that takes a function f and produces a rotated function LRf by composing f with the rotation R-1: [ LRf] =f( R− 1 x) [ L R f]= f( R − 1 x) [L R f]= f (R −1 x)
定义球面信号的旋转,即滤波器的旋转。其中,[ LRf] =f( R− 1 x) [ L R f]= f( R − 1 x) [L R f]= f (R −1 x) 这个公式的含义是:要得到经过R变换的feature map f f f 在x x x 处的值,可以通过计算在R −1 x R − 1 x R −1 x 位置上面f f f 的值。
下面是对球面和旋转群互相关的定义。
Inner products The inner product on the vector space of spherical signals is defined as: < ψ,f> =∫S 2 ∑K k= 1 ψk( x) fk (x)dx <ψ,f >=∫ S 2 k=1 ∑ K ψ k (x)f k (x)dx .
Spherical Correlation With these ingredients in place, we are now ready to state mathematically what was stated in words before. For spherical signals f and ψ ψ , we define the correlation as: [ ψ⋆f](R) =<L R ψ,f >=∫ S2 ∑K k=1 ψk( R− 1 x) fk (x) dx. [ψ⋆f ](R) = < L R ψ, f> = ∫ S 2 k= 1 ∑ K ψ k (R −1 x)f k (x) dx.
Rotation Group Correlation Using the same analogy as before, we can define the correlation of two signals on the rotation group,f ,ψ:SO ( 3) →R k f, ψ : SO (3) → R k , as follows: [ ψ⋆ f] =< L R ψ , f > = ∫ S O ( 3 ) ∑ K k = 1 ψ k ( R − 1 Q ) f k ( Q ) d Q . [ ψ ⋆ f ] = < L R ψ , f > = ∫ S O ( 3 ) k = 1 ∑ K ψ k ( R − 1 Q ) f k ( Q ) d Q .
4.快速球面卷积
It is well known that correlations and convolutions can be computed efficiently using the Fast Fourier Transform (FFT). This is a result of the Fourier theorem, which states that ^ f⋆ ψ =ˆ f ⋅ˆ ψ f ⋆ψ = f^ ⋅ ψ^ . Since the FFT can be computed in O(n log n) time and the product · has linear complexity, implementing the correlation using FFTs is asymptotically faster than the naive O(n2) spatial implementation. For functions on the sphere and rotation group, there is an analogous transform, which we will refer to as the generalized Fourier transform (GFT) and a corresponding fast algorithm (GFFT).
为了解决计算效率的问题,引入快速傅里叶变换对卷积和相关做计算,将一般的卷积转换为频域的乘积。考虑到球面和旋转群上的函数,使用广义傅里叶变换(GFT)和广义快速傅里叶变换(GFFT)。
Conceptually, the GFT is nothing more than the linear projection of a function onto a set of orthogonal basis functions called “matrix element of irreducible unitary representations”. For the circle (S1) or line ®, these are the familiar complex exponentials exp(inθ). For SO(3), we have the Wigner D-functions D l mn ( R) D mn l (R) indexed by l ≥ 0 and -l ≤ m; n ≤ l. For S2, these are the spherical harmonics Y l m Y m l indexed by l ≥ 0 and -l ≤ m ≤ l.
广义傅里叶变换就是将函数线性投影到一组正交基函数上。作者引入了量子力学中的Wigner D-函数对SO(3)群采用广义的傅里叶展开,得到一系列矩阵。能用Wigner大D矩阵是因为它是正交且完备的,所以可以用它来对SO(3)上的函数做线性展开。对于S2来说,它并不是一个群,所以它没有不可约表示(也就是不能线性投影到正交基函数上),但是它可以看成群SO(3)和SO(2)的商,所以可以用 Y l m =D l m0 ∣S 2 Y m l = D m0 l ∣ S 2 对S2展开。
如此,我们就可以定义一个信号的广义傅里叶变换:⬇
Denoting the manifold (S2 or SO(3)) by X and the corresponding basis functions by Ul (which is either vector-valued (Yl) or matrix-valued (Dl)), we can write the GFT of a function f :X→R f: X→ R as ^ fl =∫ X f( x) ‾U l ( x) dx f l ^ = ∫ X f( x) U l (x) dx
上式广义傅里叶变换中存在积分运算,为了有效计算这个积分,作者引入了广义快速傅里叶变换。在参考文献SOFT: SO(3) Fourier Transforms 中介绍了这种算法。将输入图像离散成一个数据向量s,然后乘以维格纳小d矩阵d和相应的正交权重w,得到的结果就是s的傅里叶变换ˆ s s ^ 。

在解决广义傅里叶变换定义和计算的基础上,就可以对球面相关算法进行实现。针对SO(3)计算复杂度达O(n6),作者引入了傅里叶中心切片定理进行简化。对于平面图像,傅里叶切片定理是指图像在特定角度下的一维傅里叶变换结果跟二维傅里叶变换下同样角度的切片结果一样。因此,对图像在各个角度下进行一维傅里叶变换,就可以得到二维傅里叶变换后的完整的图像。应用到球面图,也就是对图像先进行多个通道的二维S2傅里叶变换,得到的汇总结果再进行三维的SO(3)傅里叶逆变换就可以重构得到原来的图像进行SO(3)傅里叶变换后的图,也就是下图2体现的思想。
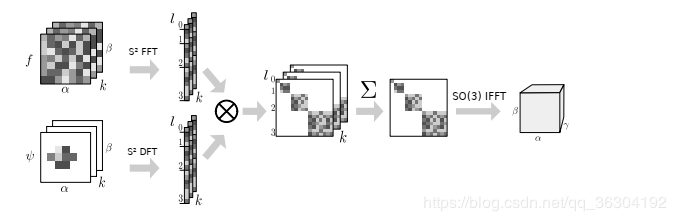
至此,作者已完成对球面卷积的理论工作,让我们做个总结。
5.总结
这篇文章的出发点是实现对球形图像的特征提取,鉴于传统神经网络的弊端,作者重新定义了卷积(互相关),由原来的平移变为旋转。考虑到球面的旋转,即三维旋转,是旋转群SO(3)的一个元素R,所以自然而然的引入群论的概念,在群论的基础上定义卷积公式。
球面卷积:[ ψ⋆f] (R) =<L R ψ,f >=∫ S2 ∑K k=1 ψk( R− 1 x) fk (x) dx [ψ⋆f ](R) = <
L R ψ, f> = ∫ S 2 ∑ k= 1 K ψ k (R −1 x)f k (x) dx
旋转群卷积 [ ψ⋆ f] ( R) =< L R ψ ,f >= ∫ S O( 3) ∑ K k =1 ψ k ( R − 1 Q ) f k ( Q ) d Q [ ψ ⋆ f ] ( R ) = < L R ψ , f > = ∫ S O ( 3 ) ∑ k = 1 K ψ k ( R − 1
Q ) f k ( Q ) d Q
可以看到区别是一个是在S2上的积分,一个是在SO(3)上的积分。
有了卷积公式如何实现呢?作者想到了傅里叶变换。众所周知,可以用傅里叶变换来求卷积,即空间域两个信号的卷积的傅里叶变换等于频域两个信号的傅里叶变换相乘。所以思路是分别求得两个信号的傅里叶变换,相乘的结果做个逆变换就可以得到两个信号卷积的结果。
如此,问题又来了,信号的傅里叶变换怎么求。这里,作者用广义傅里叶变换(GFT)解决,将S2上的信号(即图像和滤波器)线性投影到球谐函数上,SO(3)上的信号(输出的feature map)用维格纳矩阵表达。得到的结果就是傅里叶变换的结果,即: ^ fl =∫ X f( x) ‾U l ( x) dx f l ^ = ∫ X f(x ) U l (x) dx
最后再用广义快速傅里叶变换(GFFT)计算这个积分。最后一步的逆变换公式如下:f
(R )= ∑b l =0 ( 2l+ 1) ∑l m =−l ∑ l n =−l ˆ f l m n D l m n ( R) , f(R )= l =0 ∑ b (2l + 1) m =− l ∑ l n =− l ∑ l f ^ m n l D m n l ( R ) ,
求得的结果就是在旋转R作用下图像和滤波器卷积的结果。
6.Q&A
看完这篇文章,还有些细节的东西,我不是很清楚,于是发了封邮件请教了下作者Cohen,下面是问题和回答。
Q1:(S2和SO(3)上的函数到底是什么?) I know that the functions on S2 are spherical images and filters, on SO(3), they are feature maps, but how to express these functions? I can not
image these functions, especially the functions on SO(3). What the forms of these functios?
A:We store the signal as a set of values f(x_i) at a fixed set of grid points x_i. See the code for details on the grids we use. The Fourier transform then maps these samples to a vector/matrix of spectral coefficients. To mentally
visualize a function on SO(3), you can imagine a sphere with at each point a circle attached. The point on the sphere indicates the rotation axis, and the point on the circle attached to that point indicates the rotation angle.
A feature map on SO(3) just says for each rotation, how much the input “looks like” the filter, when the filter is rotated by that rotation. Another way to visualize a SO(3) feature map is as a bunch of spherical maps. Each spherical
map corresponds to a particular orientation of the filter (gamma rotation), which is applied to each point on the sphere.
(因空间任意转动可绕某一轴顺时钟转动角度θ θ ∈[0,π π ]来完成,所以SO(3)可以用一个半径为ππ的球表示,此球内的一点Q表示一个绕OQ为轴转动角度为|OQ|的转动。)
Q2:(哪里体现了滤波器的旋转?)How do the filiters rotate? The discribition of the S2-FT is “The signal f and the locally-supported filter are Fourier transformed, block-wise tensored…”, so where the rotation of filters, do the fouriers expansion represent the rotated filters?
A:We don’t explicitly rotate the filters. The operation we perform (convolution in the spectrum) is mathematically equivalent to the convolution defined in terms of rotating filters. If you want to understand the general idea, I recommend
you study the Fourier convolution theorem: https://en.wikipedia.org/wiki/Convolution_theorem . The ordinary convolution theorem is about translational convolutions, but the idea is the same. You can do a convolution by: Fourier transforming the
two signals, taking a product of the result, and then inverse Fourier transforming. The result is the same as what you get by translation (or in our case:rotating) the filter and computing inner products.
我们不显式旋转滤波器,我们的做法(频谱中的卷积)在数学上等同于旋转滤波器定义的卷积。