堆的基本概念
堆是一棵二叉树,且是一棵完全二叉树。什么是完全二叉树?先介绍一下什么是满二叉树,满二叉树是指除最后一层叶节点没有子节点外,其余每个节点都有两个子节点的二叉树。如下图所示:
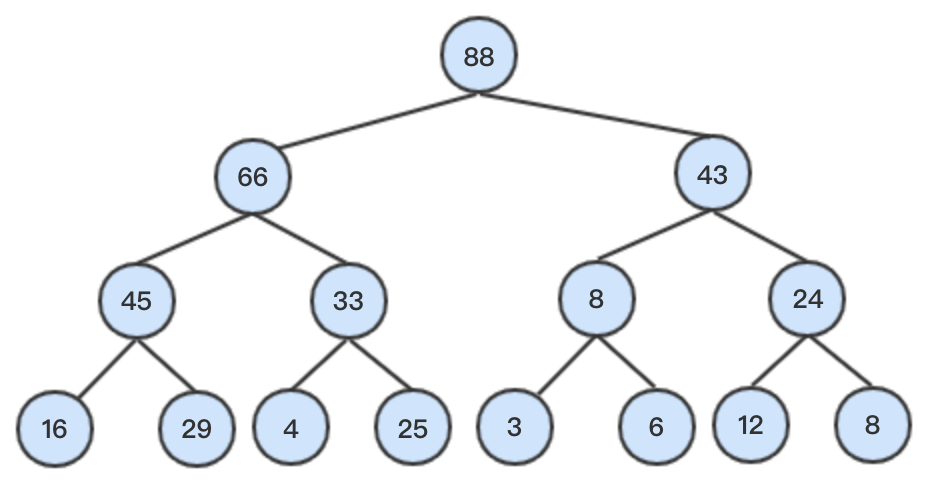
满二叉树一定是一棵完全二叉树,当满二叉树最后一层不满时,且最后一层从左到右都为连续的,则被称为完全二叉树,下面几种都是完全二叉树。
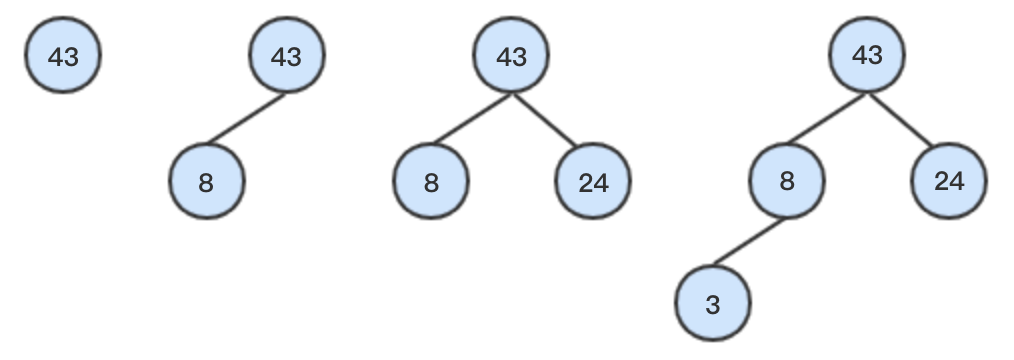
堆的性质
由于堆是完全二叉树,从完全二叉树的根节点开始,从上到下,从左到右依次从0开始编号。
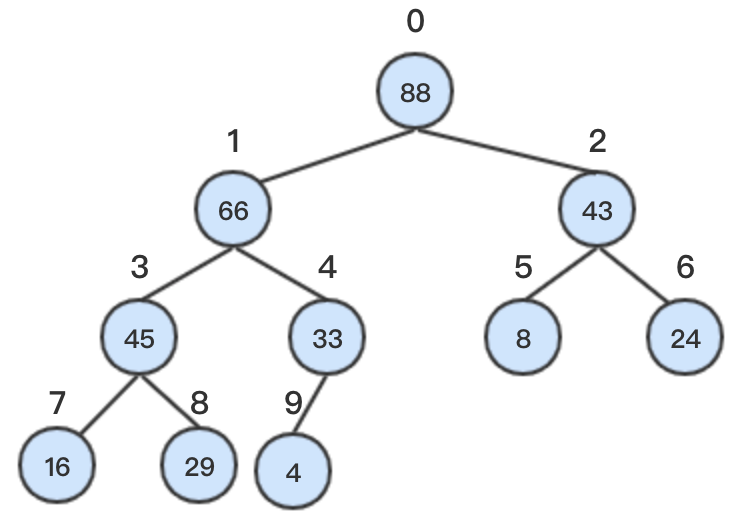
观察编号规则我们可以得出一条重要结论:如果完全二叉树的某一节点编号为n,则其左子节点(如果存在)编号为2n+1,其右子节点(如果存在)编号为2n+2,其父节点(如果存在)编号为(n-1)/2。

从上图可以看出,堆作为一棵完全二叉树,其存储结构可以直接使用数组进行存储,数组的下标即为堆的节点位置标号。
大顶堆与小顶堆
堆的这种看似无序的数据结构,如果给堆中父节点和其子节点增加某种规则,则可以生成两种非常有用的结构:大顶堆和小顶堆。
大顶堆:父节点的键值大于等于任一子节点的键值。
小顶堆:父节点的键值小于等于任一子节点的键值。
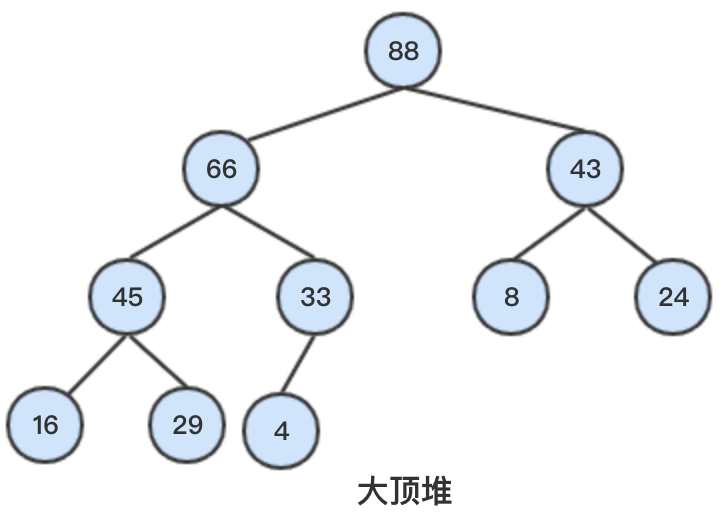
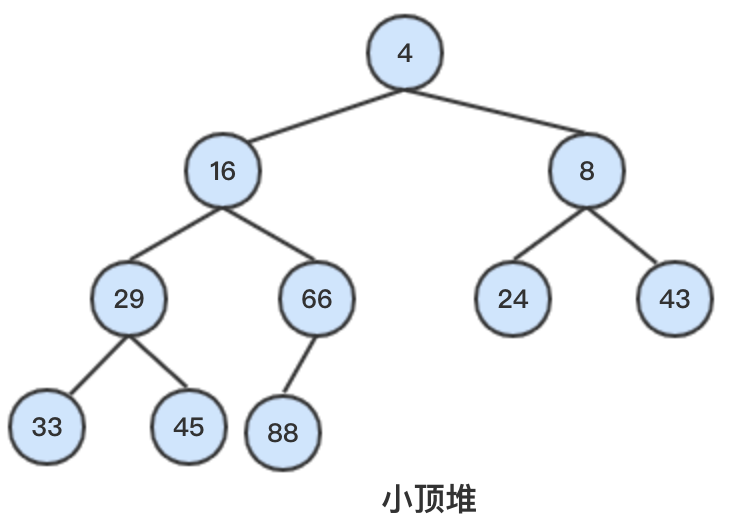
因此,大顶堆根节点是堆中最大的节点,其他节点都小于等于根节点;小顶堆则相反。
堆的算法
结合堆的数组存储结构和大小顶堆的定义,堆的操作主要为“添加元素”和“删除元素”。本文以大顶堆为例,介绍堆操作的实现原理。
添加元素
如果堆为空,则直接创建堆的根节点;若不为空,假设堆为[88,66,43,45,33,8,24,16,29,4],添加76,则需要执行以下步骤:
将该元素添加在堆末尾;
比较该元素和其父节点,若大于父节点,则与父节点交换后,再和新的父节点比较,如果还大于父节点,则继续交换,直到没有父节点或者小于等于父节点为止。
step1: 先将76添加到堆末尾
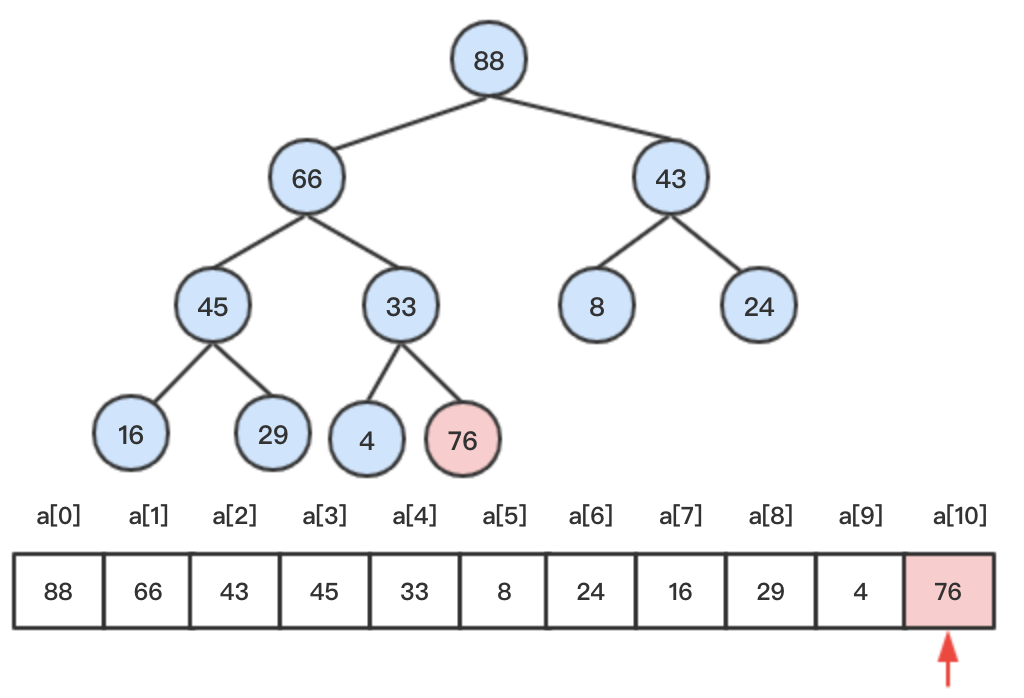
step2:比较其与父节点大小,76 > 33,交换两者位置,继续向上比较。
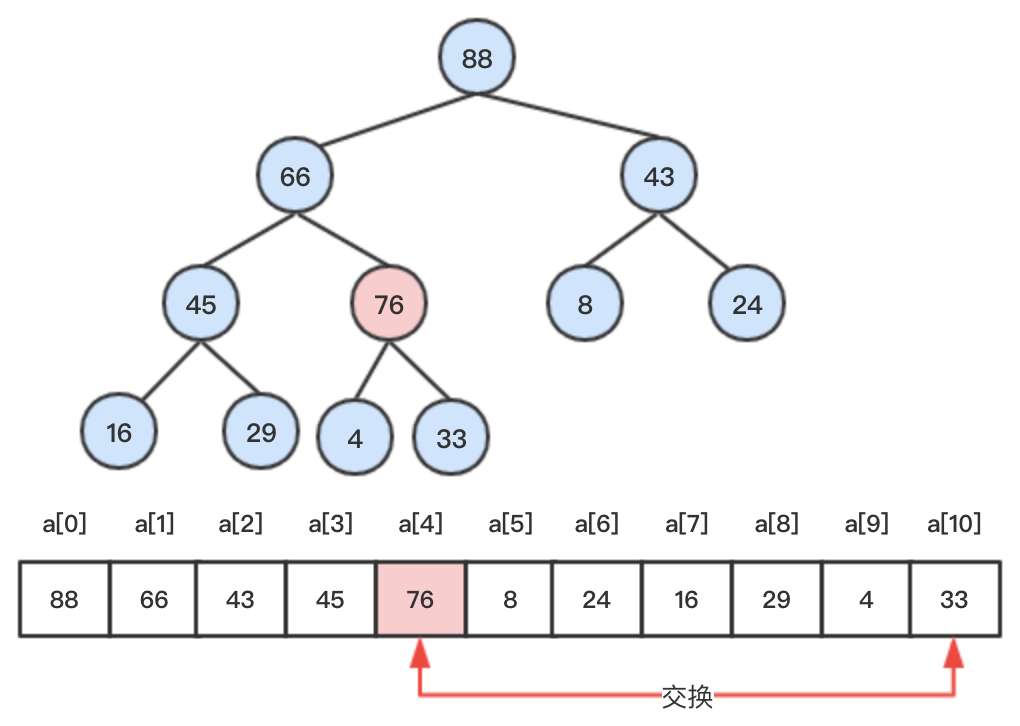
step3: 继续比较其和父节点大小,76 > 66,交换两者位置,继续向上比较。
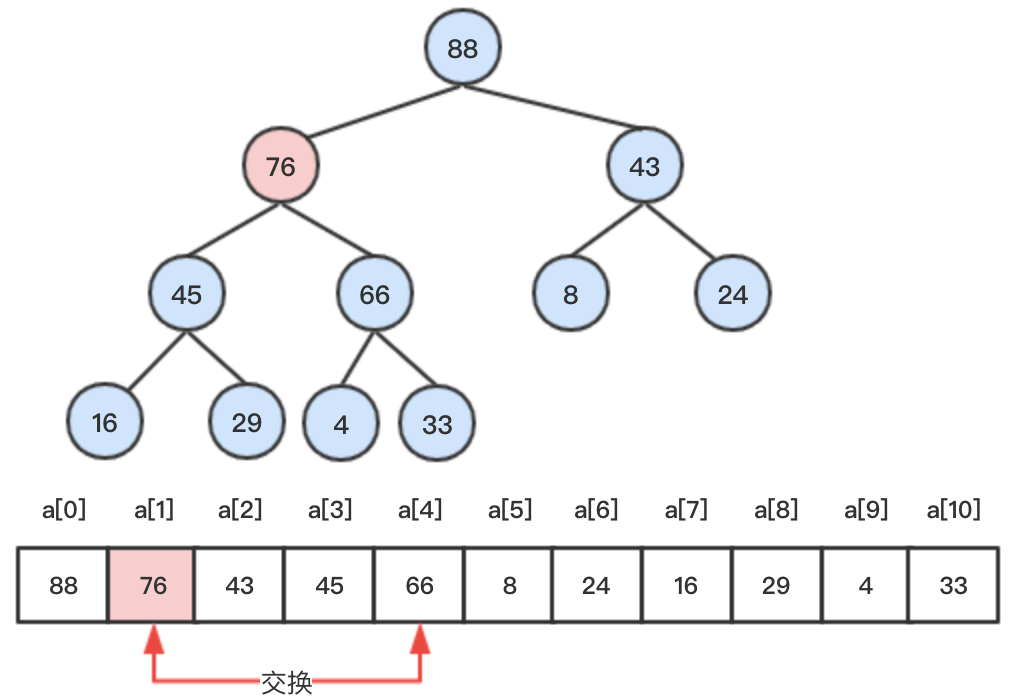
step4:继续比较,此时该节点小于其父节点,向上比较结束,添加的元素76找到了最终的位置。
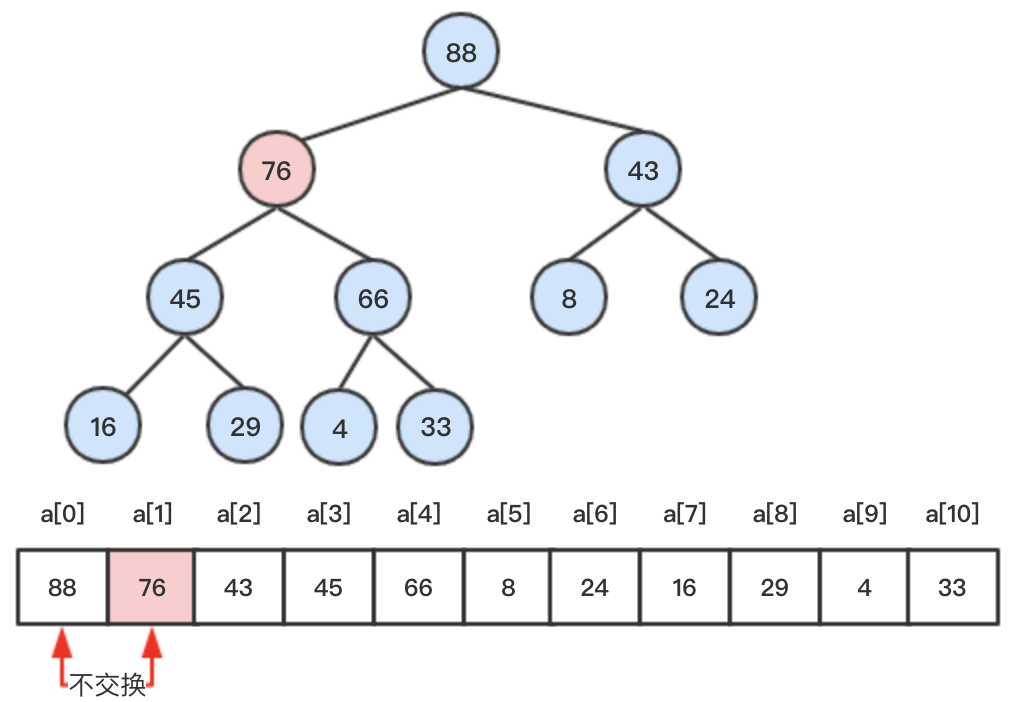
可以看出,堆中添加一个元素,需要比较交换的次数最多为该堆的高度,即log2(N)。这种自底向上调整使得重新满足堆的性质过程,我们称为向上调整(siftUp)。
删除元素
堆删除元素与添加元素不同,添加元素始终先添加在堆末尾,然后再向上调整至结束;而删除元素则可以是删除堆中任一位置的元素。下面以大顶堆为例介绍堆中删除元素操作的实现原理。
1、当删除的节点是根节点时,操作如下:
将待删根节点和堆尾节点交换后删除;
此时将新的头节点与其左右子节点比较,将其中较大的节点与头节点比较交换;此时再比较该被交换下来的“头节点”和其子节点,并继续比较交换,直到其无左右子节点或大于等于任一子节点为止。
这种自顶向下调整的过程,我们称为向下调整(siftDown)。
step1: 待删除元素88为堆的根节点。
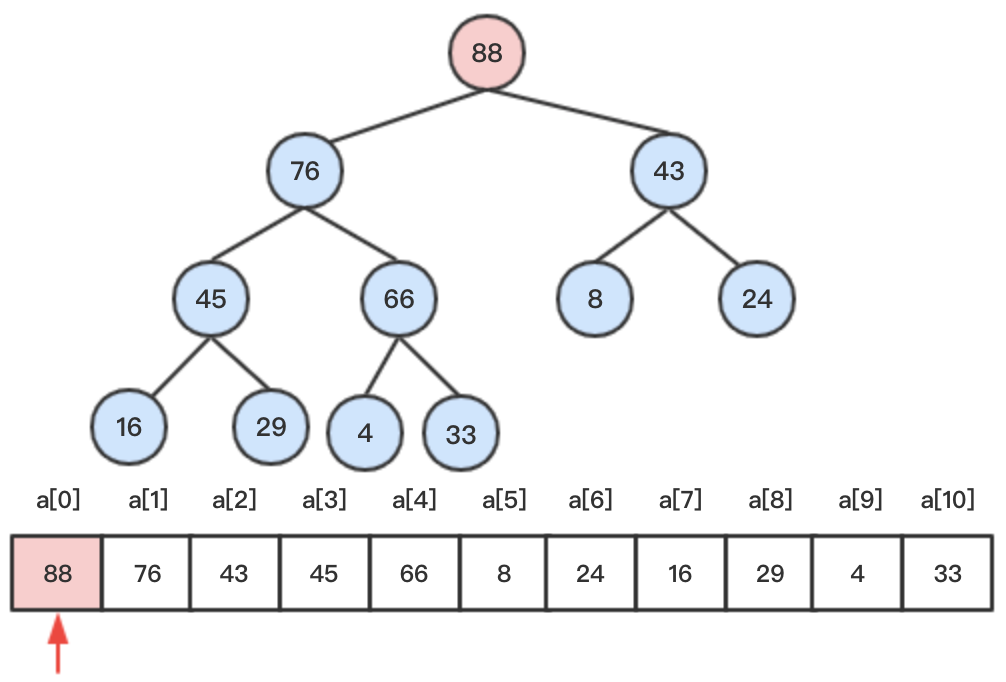
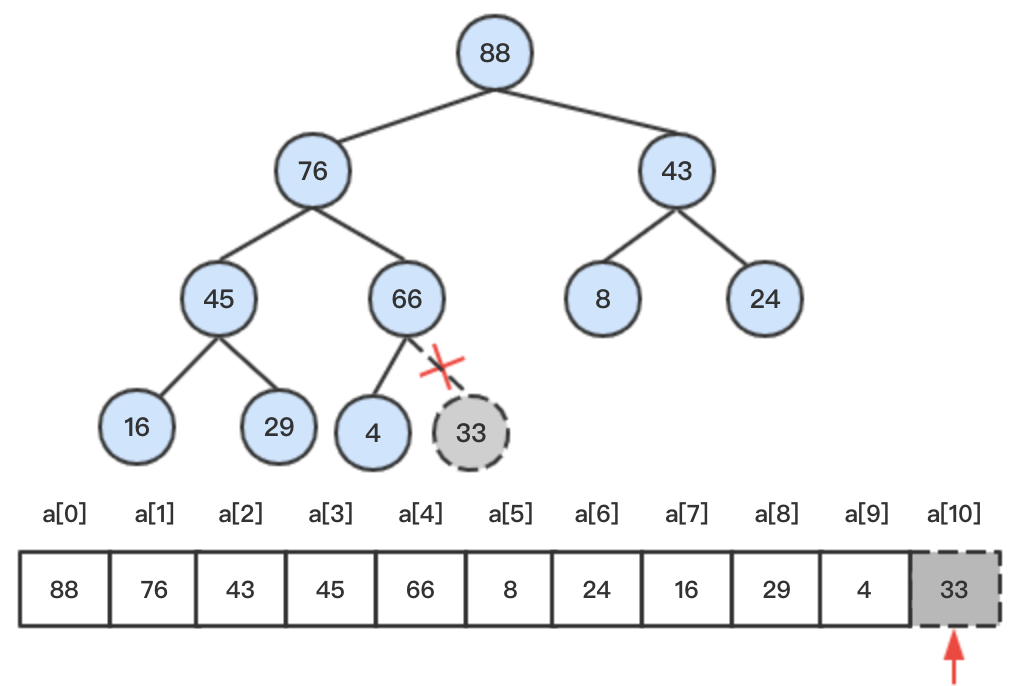
steps2:将堆尾节点33和待删除的根节点88交换后,删除堆尾节点88。
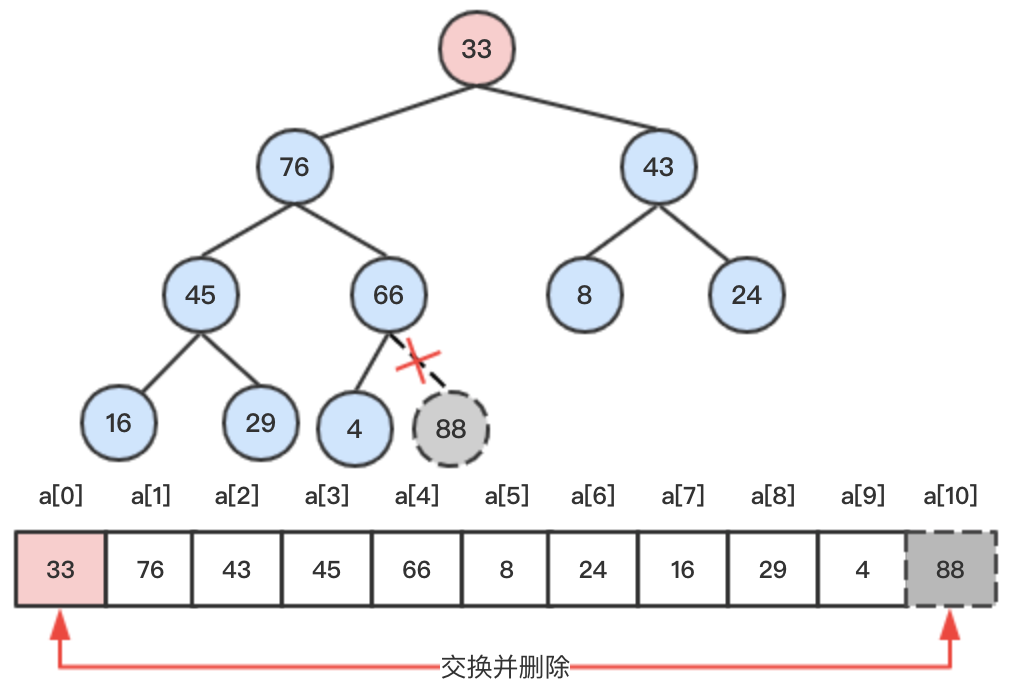
step3:比较33和其左右子节点76和43,将较大76和33进行比较,大于33,交换76和33的位置。
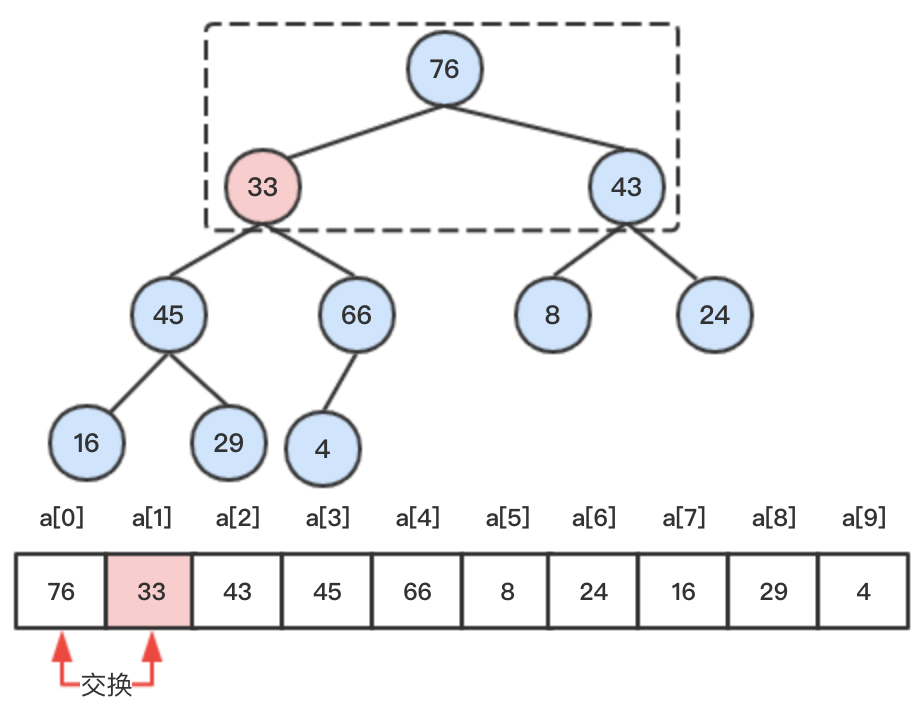
step4:继续比较33和其左右子节点45,66,将较大的66和33比较,大于33,交换66和33的位置。
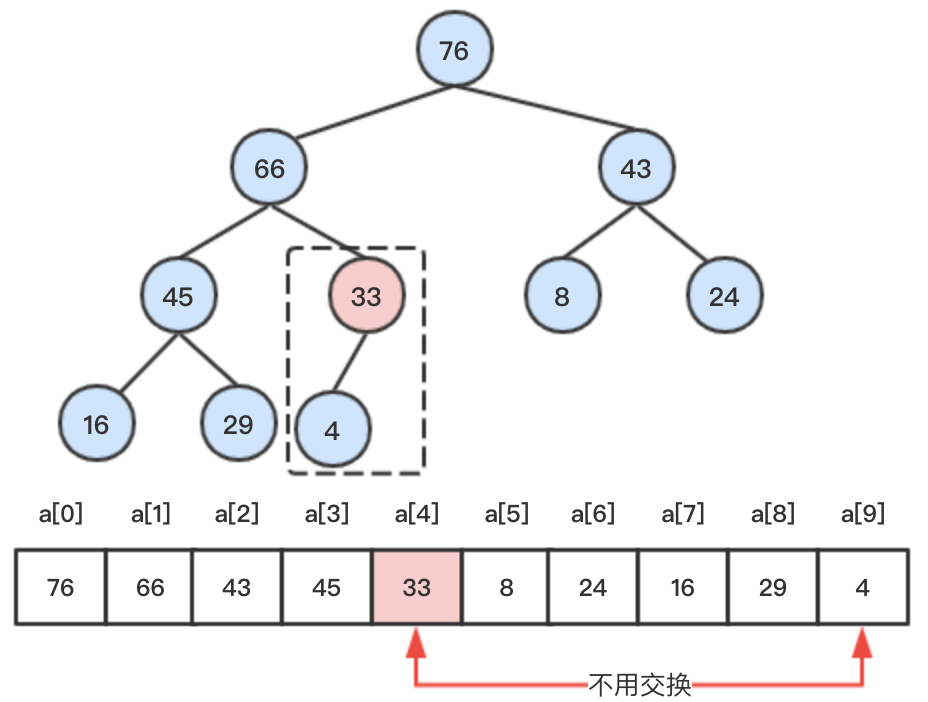
step5:继续比较33和其左右子节点4,其只有一个节点,且33>4,则无需交换,向下比较结束。
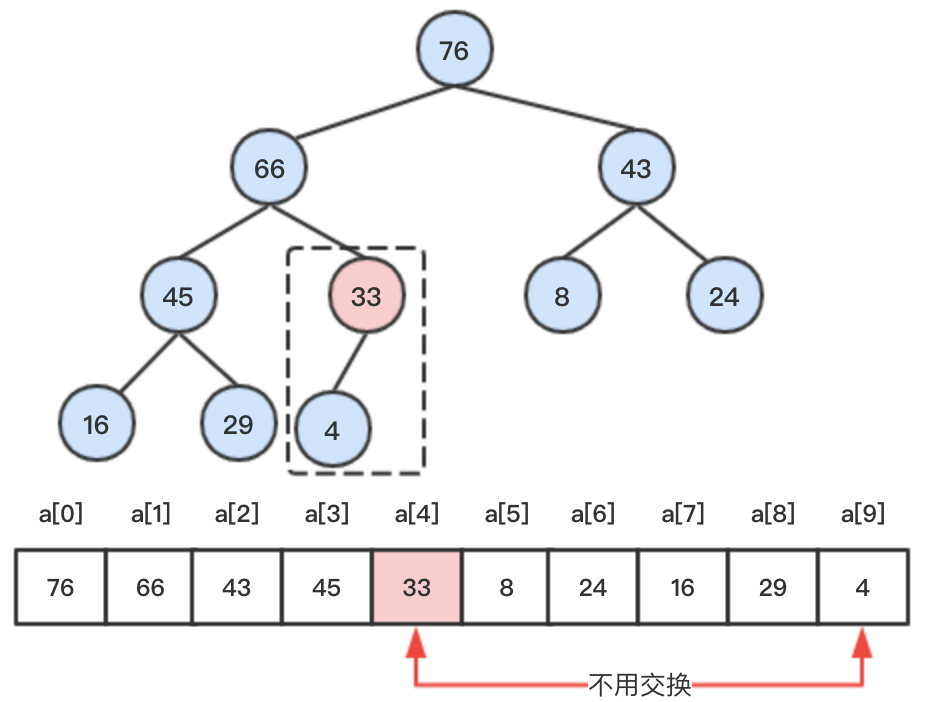
2、当删除的节点是中间某节点时,操作如下:
与删除根节点一样,将待删节点和堆尾节点交换后删除。
由于被删除的是中间节点,若交换后节点大于其父节点,则与其父节点交换并进行向上调整(siftUp)直至调整结束;若交换后节点小于其子节点,则将其中较大的子节点与其比较交换并进行向下调整(siftDown)直至调整结束。
step1:待删除元素76为中间节点。
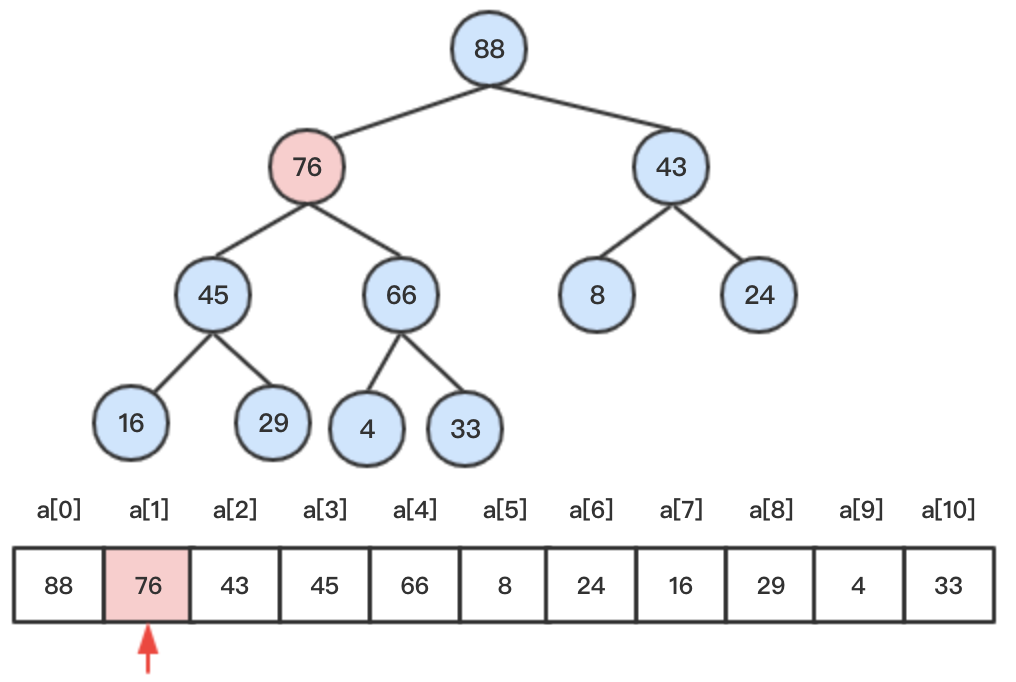
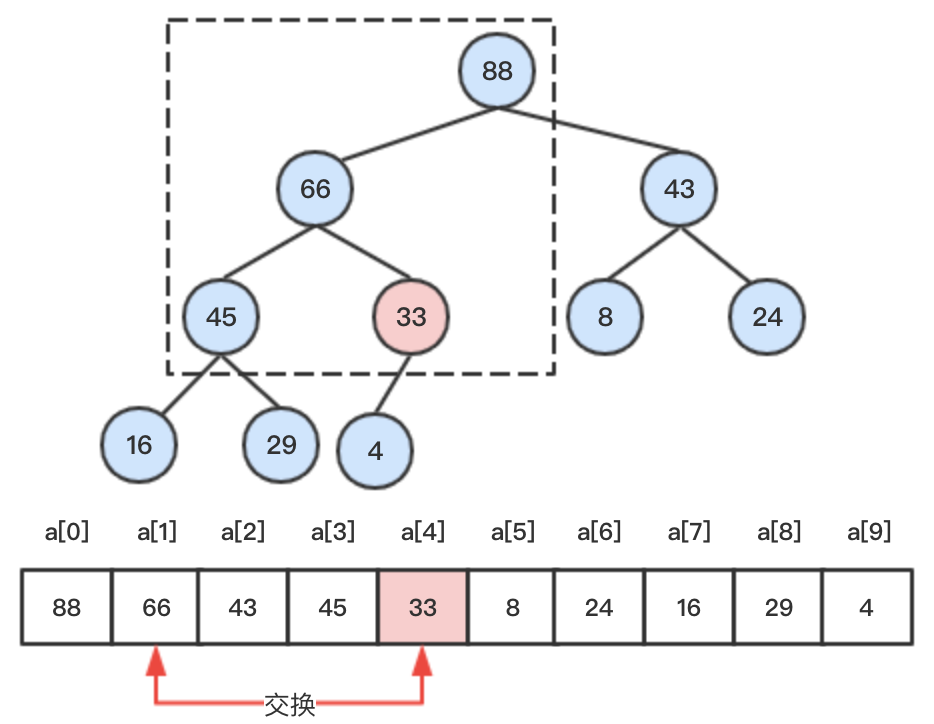
step2:将待删节点76与堆尾节点33交换后删除。
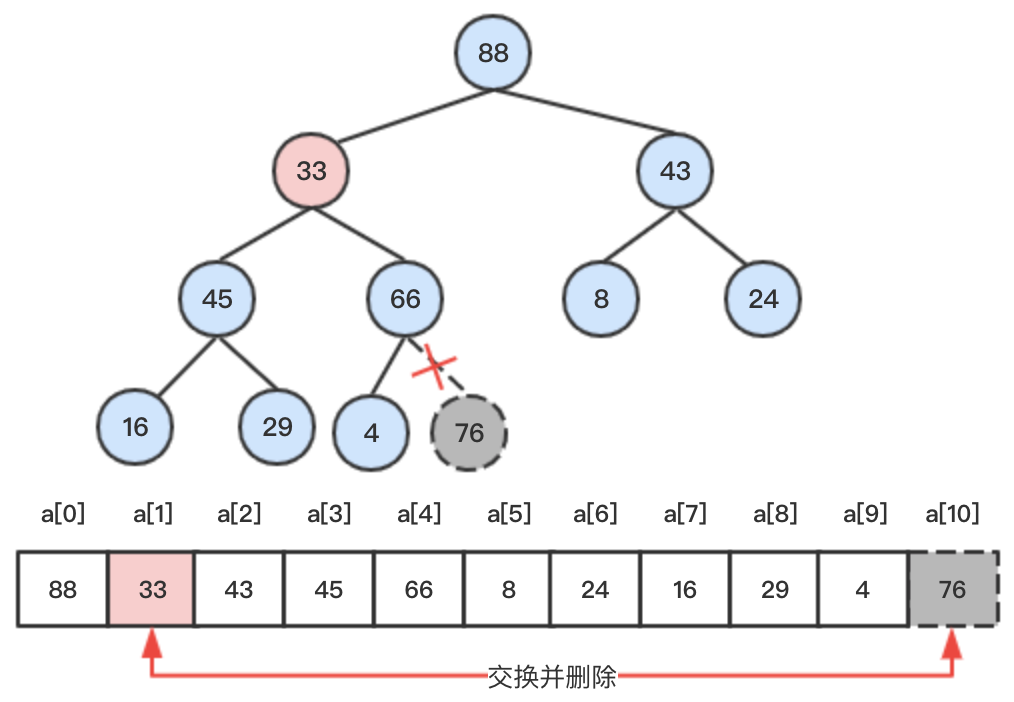
step3:交换后的33节点小于其父节点88,满足大顶堆的性质,则无需向上调整;则将其与子节点进行比较,向下调整,将其中较大的子节点66和33比较交换位置。
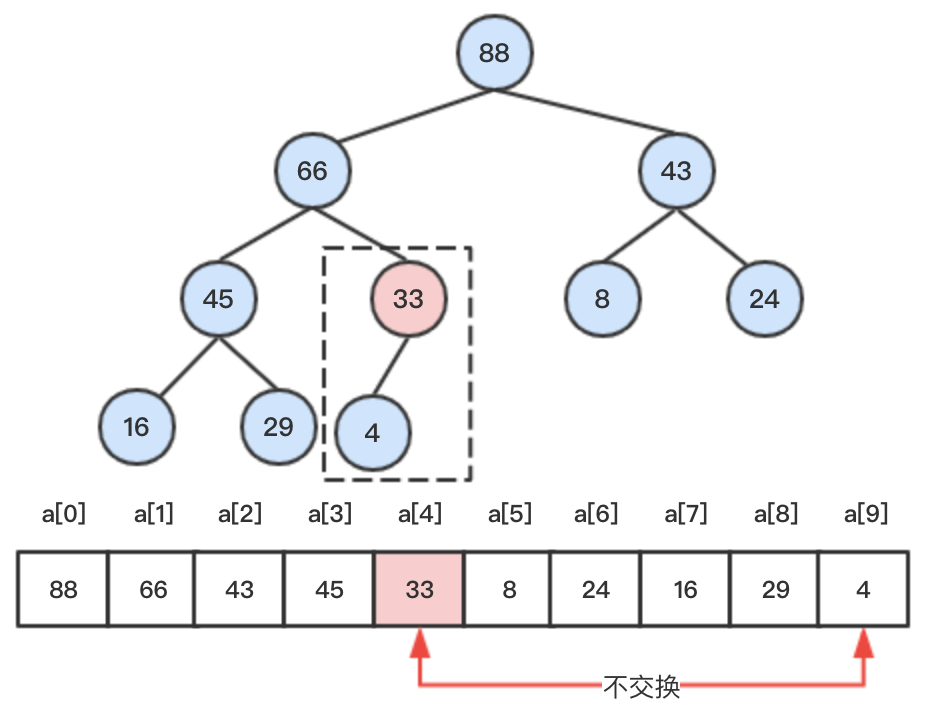
step4:将33继续进行向下调整,33大于其子节点,则调整结束。
3、当删除的节点是堆尾节点时,则直接删除即可,因为并不会影响堆的性质。
堆的算法实现
从前文可知堆的操作始终围绕两个核心过程:向上调整(siftUp)和向下调整(siftDown)。以大顶堆为例实现代码如下:
/**
* arr[i],父节点arr[(i-1)/2]
**/
private void siftUp(int i) {
int parent = (i - 1) / 2;
while (parent >= 0) {
if (((T)elements[i]).compareTo((T)elements[parent]) > 0) {
swap(elements, i, parent);
i = parent;
parent = (i - 1) / 2;
} else {
break;
}
}
}
/**
*arr[i],其子节点为 arr[2i+1],arr[2i+2]
*/
private void siftDown(int i) {
int l = 2 * i + 1;
while (l < count) {
//假定l是最大的
int r = l +1;
//将最大的设置为l
if (r < count && ((T)elements[r]).compareTo((T)elements[l]) > 0){
l = r;
}
//最大的child比较交换
if (((T)elements[l]).compareTo((T)elements[i]) > 0){
swap(elements,l,i);
i = l;
l = 2 * i + 1;
}
}
}完整代码
https://gitee.com/programmer_online/codes/7vgta3ymekr80ucx2fjnq33
总结
本文主要讲述了堆的数据结构,及其元素添加、删除算法的实现原理,最后给出了完整代码。下一篇将介绍堆在Java中的实现:PriorityQueue(优先级队列),随后我们可以轻松搞定关于大小堆的大部分算法难题。
欢迎关注公众号:程序员修仙,收看更多精彩修仙内容!
