机器学习实战：贝叶斯垃圾邮件判断APP

前言

在数据大爆炸的时代每个人每天都会收到大量的垃圾邮件，由于用传统的判断方式不好辨别，而通过使用贝叶斯可以准确的辨别垃圾邮件。

贝叶斯公式

其中B1,B2,...,Bn为完备事件组 P(A)表示：事件A发生概率 P(B)表示：事件B发生概率 P(A∩B)表示：事件A与事件B同时发生的概率 P(A|B)表示：在事件B发生的情况下，事件A发生概率

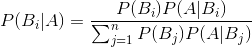
贝叶斯公式推导

因为

所以

因此

所以

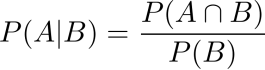
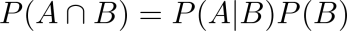
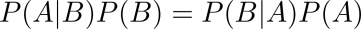
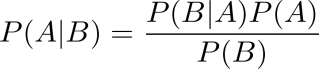
贝叶斯推断

先验概率：事件B发生之前，对事件A的一个判断 后验概率：事件B发生之后，对事件A的重新评估 可能性函数：调整因子，使得预估概率更接近真实概率

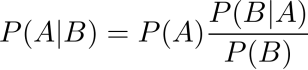
后验概率 = 先验概率 ✖️ 调整因子

这就是贝叶斯推断的含义。我们先预估一个先验概率，然后加入实验结果，看这个实验到底是增强还是消弱了先验概率，由此得到更接近事实的后验概率。

辨别垃圾邮件

假设

事件A1：为垃圾邮件事件 事件A2：为正常邮件事件 事件B ：为邮件中包含发票这个词的事件

待求

包含发票这个词的邮件是垃圾邮件的概率即P(A1|B) 包含发票这个词的邮件是正常邮件的概率即P(A2|B)

结论

如果 P(A1|B)-P(A2|B) > 0 表示包含发票这个词的邮件是垃圾邮件的概率比正常邮件大 因此判断它为垃圾邮件,反之为正常邮件。

因为P(A1|B)-P(A2|B) 等价于 P(B|A1)P(A1) - P(B|A2)P(A2)所以通过求P(B|A1)P(A1) - P(B|A2)P(A2)就可判断当前邮件是不是垃圾邮件

其中

P(A1)：为垃圾邮件概率

P(A2)：为正常邮件概率

P(B|A1)：为垃圾邮件中包含发票的概率

P(B|A2)：为正常邮件中包含发票的概率

贝叶斯应用

其中

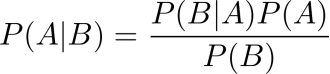
P(A1)：为垃圾邮件概率

P(A2)：为正常邮件概率

P(B|A1)：为垃圾邮件中包含发票的概率

P(B|A2)：为正常邮件中包含发票的概率

为什么要用贝叶斯

P(A1|B)：包含发票的邮件是垃圾邮件的概率（无法统计） P(B|A1)：垃圾邮件中包含发票这个词的概率（可以统计）

通过贝叶斯我们可以把不可统计的P(A1|B)转换成可统计的P(B|A1)。

运行结果

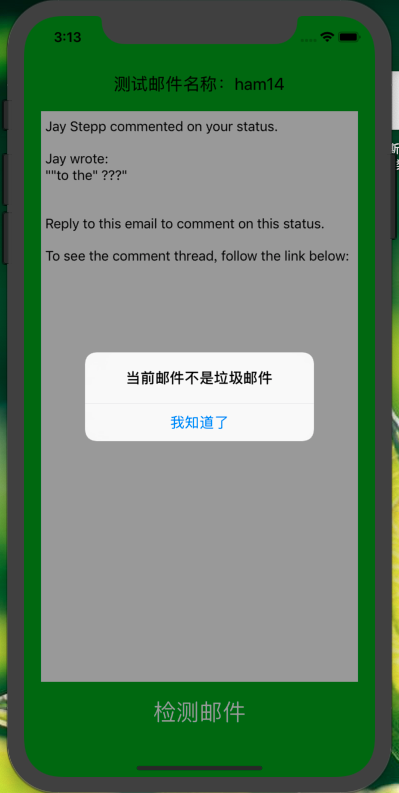
项目介绍

因为本人比较喜欢Swift这门编程语言，因此本项目代码全部由Swift实现。

如果喜欢请点个赞！谢谢

Github地址