黎曼猜想在 2019 年的新进展：Jensen-Polya (Hyperbolicity) 道路

刚才谈到 RH，朋友告知 2019 年的进展情况：

初看很厉害，打个比喻，似乎进展已经到了 twin prime conjecture 的程度了（自张益唐以后的程度）。当然，现在一群数论猜想都卡在最后的程度，所以也说不定最后需要多久。

细看感觉希望不大，用的都是传统的解析数论估计，还没用上 deep results。群友说 Ono 也感觉这个希望不大。不过，我相信黎曼猜想最终是会靠非常"技术"的方法证明，很难有简短的"奇妙证明"。

1. 论文的结论

本文先大致介绍论文的结论，然后再介绍证明的逻辑。

首先 Jensen-Polya 在上世纪二十年代证明了 RH 等价于对应的 Jensen 多项式 的 hyperbolicity（意思是 的根都是实数）对于所有 和 都成立。

相关的图，红色的都在实数轴上：

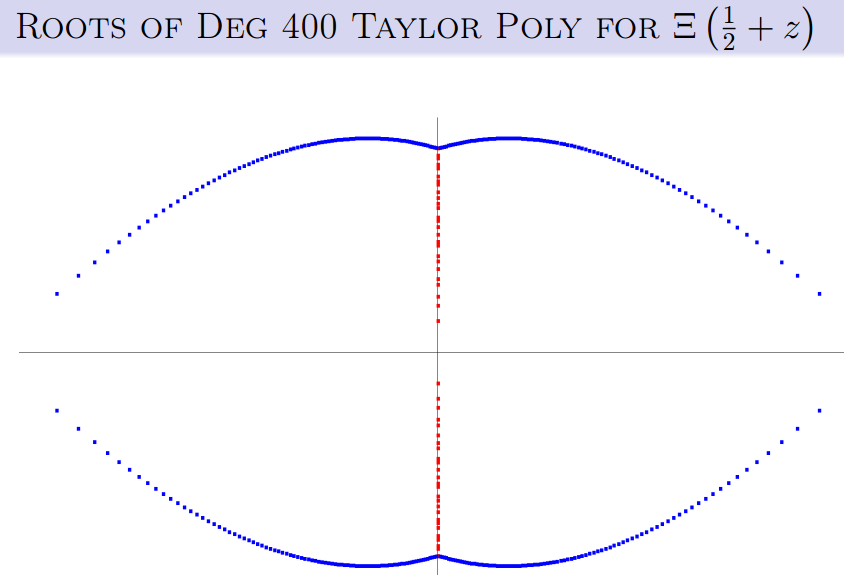
回到 Jensen 多项式 ，之前有人证明了这对于 和所有 都成立。

而 Griffin-Ono 在此证明了这对于所有 和充分大的 n 都成立。也顺便证明了这对于 和所有 都成立。

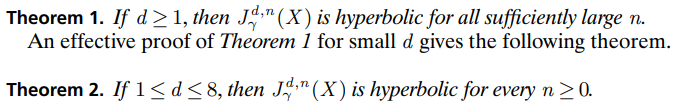
简单地说，Hermite 多项式都具有 hyperbolicity，文中证明 在 时趋近于 Hermite 多项式。所以我们需要充分大的 n。

是不是貌似很接近了？如果能把"充分大"去掉就证明了 RH。

例如，有可能最终再证明这对于所有 和 都成立（这个过程可能需要找到方法用上目前各个领域最强的结果，可能包括 Langlands 那边的），然后再用电脑验算一遍所有 的情况，就证明了 RH。

然而如前所述，文章的方法似乎太传统，所以可能希望不大。

2. 论文的证明过程

作者描述的证明过程：

Thm1 ：主定理，zeta 满足 d>=1 hyperbolic（all but finite many n）

Thm2：Thm1 的细化：在 8 >= d >=1 时，对于所有 n 成立

下面开始证明，首先：

Thm3 => Thm4

Thm3：某条件 => 趋近于 Hermite（而 Hermite 是 hyperbolic）

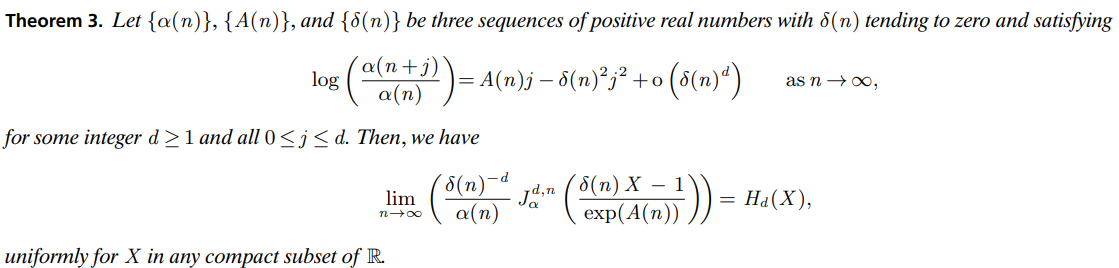
Thm4：是 Thm3 的推论，前述条件 => hyperbolic（all but finite many n）

Thm3 => GUE（随机矩阵那边的结果）

于是需要证明 zeta 满足前述的条件，实际上模形式也满足：

Thm4 + Thm9 => Thm1

Thm9：zeta 满足 前述条件【若 d>=2 】

Thm5：dedekind eta 满足 d>=1 hyperbolic（all but finite many n）

Thm7：weakly holo. form 满足 d>=1 hyperbolic（all but finite many n）它包括了 Thm5

Thm8：还有更多类型的系数，满足类似的情况（不过不一定有 hyperbolic）

以上是作者在 Sec1 描述的证明过程。实际的证明过程：

Sec2：证明 Thm3，是 Thm8 的特例，Thm8 的证明很短。

Sec3：证明 Thm7，是用 Poincare series & Bessel 证明 weakly holo. form 满足 Thm3 的性质，也很短。

Sec4：证明 Thm9，是从 theta 开始，先到 [12]，再用一些逼近和截断。

然后注意到 [12] => [13]，然后 [13] + Thm9 => [14]

Sec5：证明 Thm1。首先 [13] + [14] + Stirling => [16] => [17] => [18] => [15]，然后 [15]+Thm3 => Thm1

证明 Thm2。用了其它一些论文中的验算。