LeeCode - 斐波那契数
题目:
斐波那契数,通常用 F(n) 表示,形成的序列称为斐波那契数列。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0, F(1) = 1 F(N) = F(N - 1) + F(N - 2), 其中 N > 1. 给定 N,计算 F(N)。
示例 1:
输入:2 输出:1 解释:F(2) = F(1) + F(0) = 1 + 0 = 1.
分析:
这题比较简单,先根据N给出到第N斐波那契数的数组,然后在数组中取值计算即可。这里要注意的是斐波那契数列从0,1开始驱动,所以这两个数我们得先给出。其次题目提交的时候会传入 F(0),这里会返回NaN,所以得分情况讨论N的值。
答案:
var fib = function(N) {
if (N < 2) return N
let arr = [0, 1]
for (i = 2; i < N; i ++) {
arr.push(arr[i - 1] + arr[i - 2])
}
return arr[N - 1] + arr[N - 2]
};
结果:提交成功
耗时:80ms
内存:33.7MB
经过查找资料,这道题讲的是动态规划算法,而我写的方法,就是动态规划算法,但是我其实没有考虑到计算复杂度,纯粹是因为我第一时间想到这个方法。什么是动态规划算法?这里从暴力递归开始讲起。。。
暴力递归解法
var fib2 = function(N) {
if(N < 2) return N
return fib2(N - 1) + fib2(N - 2)
};
这是一个非常简洁的函数,也非常容易看懂。但是可以发现,当N=50的时候,得先分别计算fib2(49)和fib2(48),而计算 fib2(48)又需要计算fib2(47)和fib2(46)。。。如此循环重复计算多次,画出递归树:
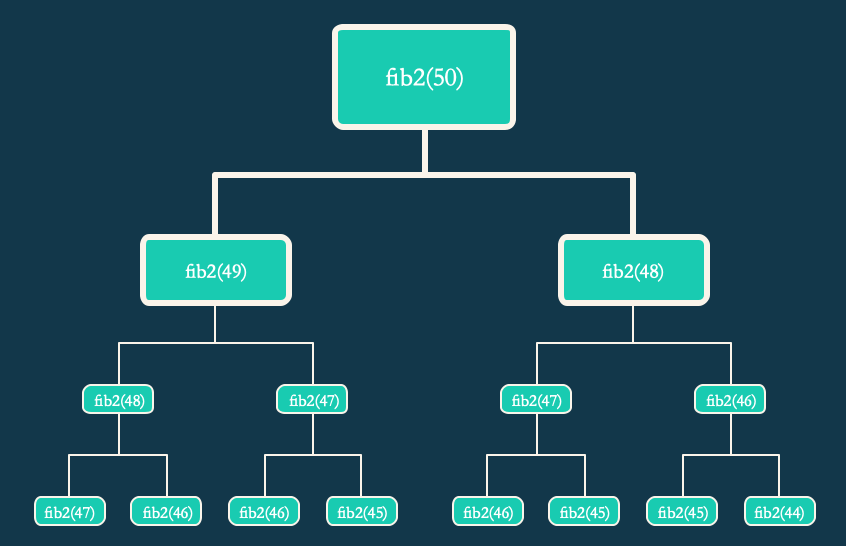
这里使用一个测试函数,打印一下计算时间:
// 测试时间的函数
function test(fun,n){
console.time()
fun(n) // 执行函数
console.timeEnd()
}
test(fib, 50) // 0.29ms
test(fib2, 50) // 这里电脑卡死了。。。0·0
// 换一个小点的
test(fib, 40) // 0.22ms
test(fib2, 40) // 1165.78ms
可以看到fib2()方法计算复杂度是爆炸增长的。
解决一个子问题的时间,在本算法中,没有循环,只有一个加法操作,时间为 O(1)。子问题个数,即递归树中节点的总数。显然二叉树节点总数为指数级别,所以子问题个数为 O(2^n),所以这个时间复杂度为 O(2^n)。
而带字典的本质就是,将计算内容及结果存入数组,下次计算前先去数组寻找是否存在,如果存在则直接取值跳过重复计算。
在这题里,我的算法思路都是一样的,是先进行一遍计算到f(N),存入数组,等于只计算了一次,时间复杂度为O(n)。
进行到这里,我突然想到,我只需要用到数组的最后两个元素,那我能不能只保存最后两个元素?
var fib3 = function(N) {
console.time()
if (N < 2) return N
let first // f(N - 1)
let second// f(N - 2)
for (i = 0; i < N; i ++) {
first = i + 1
second = i
}
console.timeEnd()
return first + second
};
fib3(40) // 0.0219ms
这是我能想到的最优解了,各位 dalao 如果有更好的方法,麻烦告诉一下我啊!谢谢 dalao