堆及堆排序(JS)

忘尘
2,641 阅读11分钟

堆及堆排序

代码实现

堆有序:当一棵二叉树的每个结点都大于等于它的两个子结点时,它被称为堆有序。

**二叉堆:**二叉堆是一组能够用堆有序的完全二叉树排序的元素,并在数组中按照层级储存(不使用数组的第一个位置)。

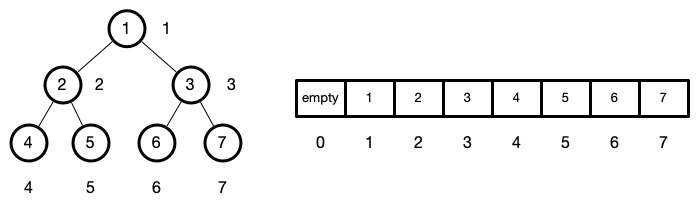
image-20190810102011914

我们的下标从1开始,下标变量为ind

那对于给定位置ind的节点:

  • 左侧节点位置是2*ind
  • 右侧节点位置是2*ind+ 1
  • 父节点位置是parseInt(ind /2)

parseInt(3/2) === parseInt(2/2) === 1

我们使用堆这个数据结构主要有三个操作

  • pusk(val):向堆中插入一个新的值
  • pop(val):弹出最值
  • top():查看最值

向堆中插入值

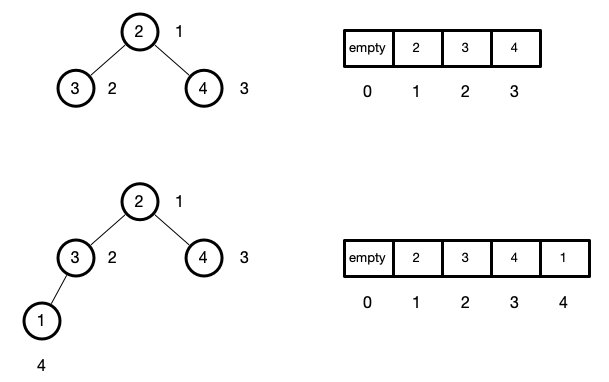
image-20190810105334293

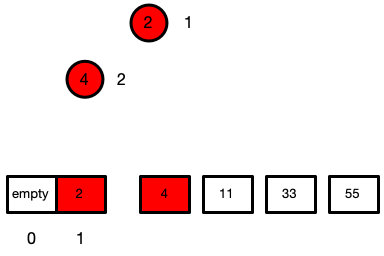
我们先假设我们堆里面已经是堆有序的,且含有的元素为2,3,4

这个时候,如果我们往里面添加1

class MinHeap {
  constructor() {
    this.heap = []
    this.len = 0
  }
  push(val) {
    this.heap[++this.len] = val
  }
}

this.heap[++this.len]先进行this.len加加后再赋值,如果此时this.len为0的话,那么实际是this.heap[1] = val

这种写法就达到了我们数组首位为空的目的

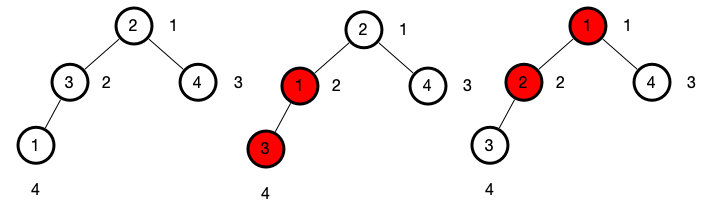
为了达到堆有序,我们应该对添加的元素进行调整,因为每次我们都是在末尾添加元素的,那我们把这个调整的过程称为上浮swim

push(val) {
  this.heap[++this.len] = val
  this.swim(this.len)
}

那我们现在来思考swim的实现,我们先却次明确堆有序的概念

堆有序:当一棵二叉树的每个结点都大于等于它的两个子结点时,它被称为堆有序。

如果我们是要实现一个最小堆,那它的父节点一定是比子节点大的,为了方便我们使用一个函数来表示比较

more(i, j) {
  return this.heap[i] > this.heap[j]
}

如果此时节点为ind那么父节点的下标就是parseInt(ind/2)

我们是想建立最小堆,所以小的值应该在更上头

如果父节点比该节点还大

那就应该交换两者的位置

然后我们不断重复该过程

直到父节点小于子节点

即达到了堆有序

那需要的条件就是

while ( this.more(parseInt(ind / 2), ind))

为 了避免当parseInt(ind / 2) === 0的时候,会对不存在的this.heap[0]进行操作

我们需要确保ind > 1

所以循环的添加应该是

while (ind > 1 && this.more(parseInt(ind / 2), ind))

image-20190810112642855

swim(ind) {
  while (ind > 1 && this.more(parseInt(ind / 2), ind)) {
    this.swap(parseInt(ind / 2), ind)
    ind = parseInt(ind / 2)
  }
}

交换元素swap的函数实现

swap(i, j) {
  let temp = this.heap[i]
  this.heap[i] = this.heap[j]
  this.heap[j] = temp
}

堆中弹出一个值

每次弹出的都是最值,即根节点,如果是最小堆就是最小值,最大堆就是最大值

根据我们上面的讲述及图,我们很容易知道最值就是

pop() {
  const top = this.heap[1]
  return top
}

但是如果把根元素直接删除的话,整个堆就毁了

所以我们思考思考着使用内部的某一个元素先顶替根节点的位置

这个元素显而易见的是最后一个元素

因为最后一个元素的移动不会使得树的结构改变

pop() {
  const top = this.heap[1]
  this.swap(1,this.len)
  return top
}

这里就会又遇到上面插入元素时遇到的问题,此时的堆可能是无序的

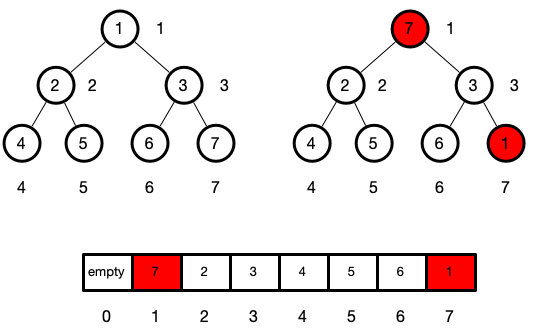
image-20190810114328765

很明显,我们是不需要缓存原本的根节点的

this.swap(1,this.len--)

这表示,我们在交换完后,就对堆的长度减一

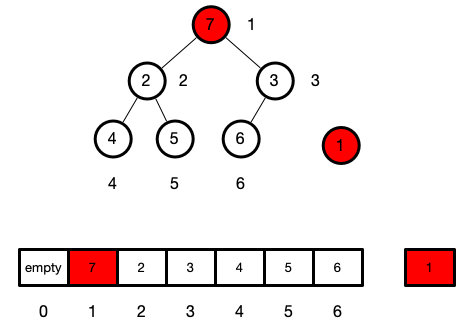
image-20190810114548824

但是实际上我们的数组里还是对该元素有引用的,因为这里我们只是让我们所谓的堆的长度删减,为了防止内存泄漏,我们需要让数组取消对该节点的引用

在真实项目中,我们存储都是一个对象里的key,所以我们需要解除对对象的引用,使其内存回收

this.heap[len + 1] = undefined

现在代码就有

pop() {
  const ret = this.heap[1]
  this.swap(1, this.len--)
  this.heap[this.len + 1] = undefined
  return ret
}

虽然现在终于去掉了这个不要的节点了,但是我们堆的有序性还是没有解决

原本这个末尾节点就是在下层的,所以此时应该也是慢慢的回到下层,我们就把这个下沉操作称为sink

同样这个操作应该也是不断循环的直至ind所指的节点下面再无元素

如果该节点子节点,下标可能就是2*ind和2*ind + 1,

所以当2*ind还在堆的长度范围内,就说明还要和子节点进行大小比较

sink(ind) {
  while (2 * ind <= this.len) { 
    // ...
  }
}

当然我们不能忽略了2*ind + 1的存在

我们是最值堆,期望的当然是把子节点中更小的往上放

所以如果2*ind比2*ind + 1还大的话,我们应该让j++,然后就会指向2*ind + 1,即更小的值

let j = 2 *ind
if (this.more(j, j + 1)) j++

这里需要考虑j此时可能就等于 this.len,那么根本就不存在j+1的元素了

所以我们需要让j < this.len,那么这样就说明一定有j+1存在

sink(ind) {
  while (2 * ind <= this.len) { 
    let j = 2 * ind
    if (j < this.len && this.more(j, j + 1)) j++
    // 此时j表示的就是子节点最小的那个了
  }
}

上面这么多只是确认与ind要判断的节点

现在我们可以开始进行判断了

如果ind比j小的话,我们就break,停止向下循环了,因为此时ind的位置就是正确的

否则,我们就交换两者的位置

然后再把ind改为交换后的位置,即j,再进行下次循环

sink(ind) {
  while (2 * ind <= this.len) { 
    let j = 2 * ind
    if (j < this.len && this.more(j, j + 1)) j++
    if (!this.more(ind, j)) break
    this.swap(ind, j)
    ind = j
  }
}

当我们把sink方法实现完后, 我们就可以完成弹出的全部操作了

pop() {
  const top = this.heap[1]
  this.swap(1, this.len--)
  this.heap[this.len + 1] = undefined
  this.sink(1)
  return top
}

查看最值及其他方法

  • top查看最值
  • size查看堆长度
  • isEmpty查看是否为空

关于堆,我们还要需要提供一个API,top让使用者知道当前的最值是多少

top(){
  return this.heap[1]
}

size() {
  return this.len
}

isEmpty() {
  return this.len === 0
}

代码展示

class MinHeap {
  constructor() {
    this.heap = []
    this.len = 0
  }
  push(val) {
    this.heap[++this.len] = val
    this.swim(this.len)
  }
  pop() {
    const top = this.heap[1]
    this.swap(1, this.len--)
    this.heap[this.len + 1] = undefined
    this.sink(1)
    return top
  }
  top() {
    return this.heap[1]
  }
  size() {
    return this.len
  }
  isEmpty() {
    return this.len === 0
  }
  swim(ind) {
    while (ind > 1 && this.more(parseInt(ind / 2), ind)) {
      this.swap(parseInt(ind / 2), ind)
      ind = parseInt(ind / 2)
    }
  }
  sink(ind) {
    while (2 * ind <= this.len) {
      let j = 2 * ind
      if (j < this.len && this.more(j, j + 1)) j++
      if (!this.more(ind, j)) break
      this.swap(ind, j)
      ind = j
    }
  }
  more(i, j) {
    return this.heap[i] > this.heap[j]
  }
  swap(i, j) {
    let temp = this.heap[i]
    this.heap[i] = this.heap[j]
    this.heap[j] = temp
  }
}

对于this.heap和this.len属性,我们显然是不想暴露的,但是js中没有私有属性,我们就用__来表示私有属性

改为this_heap和this._len

测试

我们拿LeetCode 215题测试

var findKthLargest = function (nums, k) {
  let minHeap = new MinHeap()

  for (let i = 0; i < nums.length; i++) {
    if (minHeap.size() < k) {
      minHeap.push(nums[i])
    } else if (minHeap.top() < nums[i]) {
      minHeap.pop()
      minHeap.push(nums[i])
    }
  }
  return minHeap.top()
};

通过了👌

最大堆和最小堆

最大堆与最小堆的区别就是我们在下沉或者上浮时,是让小的还是让大的上浮或者下沉

在代码中我们都是通过

sink(ind) {
  while (2 * ind <= this.len) {
    let j = 2 * ind
    if (j < this.len && this.more(j, j + 1)) j++
    if (!this.more(ind, j)) break
    this.swap(ind, j)
    ind = j
  }
}

我们注意看第5行代码if (!this.more(ind, j)) break

说明如果this.more(ind, j)为真, 就会执行后面的交换函数

  • ind指的当下元素
  • j指的是ind*2或者ind*2 + 1,即ind的子节点

如果ind比j大,就交换,所以就是把大的往下沉,最后这个堆就是一个最小堆了

more(i, j) {
  return this.heap[i] > this.heap[j]
}

如果把>改成<就是反面,即此时的最小堆变成了最大堆

那我们思考着能不能在创建的时候,通过传入参数来确定是最小堆还是最大堆呢

class Heap {
  constructor(maxOfMin = 0) {
    this.heap = []
    this.len = 0
    this.maxOfMin = parseInt(maxOfMin)
  }
  more(i, j) {
    let ret = this.heap[i] > this.heap[j]
    return this.maxOfMin === 0 ? ret : !ret
  }
}

现在默认是0,就是最小堆,如果是别的就是最大堆了

const maxHeap = new Heap(1)
const minHeap = new Heap()
let arr = [11, 2, 33, 4, 55, 6]
for (let i = 0; i < arr.length; i++) {
	maxHeap.push(arr[i])
	minHeap.push(arr[i])
}
console.log('最大堆');
console.log(maxHeap.pop());
console.log(maxHeap.pop());
console.log(maxHeap.pop());
console.log(maxHeap.pop());
console.log(maxHeap.pop());
console.log(maxHeap.pop());
console.log('最小堆');
console.log(minHeap.pop());
console.log(minHeap.pop());
console.log(minHeap.pop());
console.log(minHeap.pop());
console.log(minHeap.pop());
console.log(minHeap.pop());

最大堆
55
33
11
6
4
2
最小堆
2
4
6
11
33
55

堆排序

突然发现一个特别有趣的点,上面的输出都是有序的了,我们可以利用这一特性来对数组进行排序

function heapSort(arr) {
  let len = arr.length
  for (let i = parseInt(len / 2); i >= 1; i--) {
    sink(arr, i, len)
  }
  while (len > 1) {
    swap(arr, 1, len--)
    sink(arr, 1, len)
  }
  return arr
}

function sink(arr, ind, len) {
  while (2 * ind <= len) {
    let j = 2 * ind
    if (j < len && more(arr, j, j + 1)) j++
    if (!more(arr, ind, j)) break
    swap(arr, ind, j)
    ind = j
  }
}
function swap(arr, i, j) {
  i--; j--;
  let temp = arr[i]
  arr[i] = arr[j]
  arr[j] = temp
}
function more(arr, i, j) {
  i--; j--;
  return arr[i] < arr[j]
}

let arr = [11, 2, 33, 4, 55]
let ret = heapSort(arr)
console.log(ret);

我们来分析上面的代码

构造最大堆

function heapSort(arr) {
  let len = arr.length
  // 构造最大堆
  for (let i = parseInt(len / 2); i >= 1; i--) {
    sink(arr, i, len)
  }
  console.log('<<<===arr==>>>');
  console.log(arr);
  console.log('==>>>><<<==');
  //...
}

打印出来的结果是

[ 55, 11, 33, 4, 2 ]

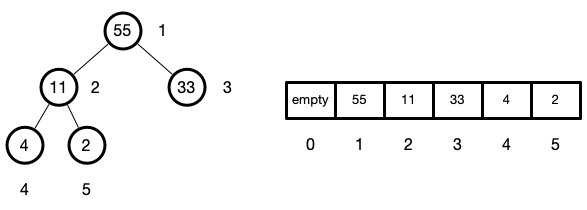
image-20190810195251898

在实际待排序的数组是从arr[0 ~ (len - 1)],而不是我们图上的arr[1 ~ len]

所以,我们在后面有个小技巧可以弥补,使得我们还是假装是在1~len间操作

那上面的代码是怎么实现使得数组转换为最大堆的呢

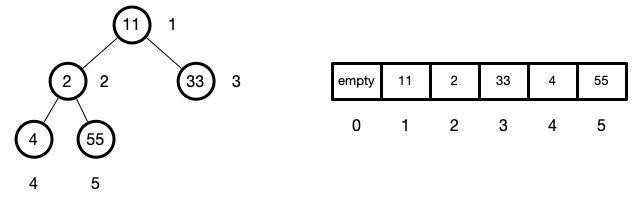
image-20190810205316757

上图是原始数组

我们从最后一个节点的父子节点开始,往上遍历

每遍历到该节点时,执行sink操作,使其下沉到属于他的位置

这样我们就可以确保每次遍历某一节点时,他的子孙节点最大的就是子节点

最后一个节点的下标就是len,那他的父节点的下标就是parseInt(len / 2)

然后我们就不断i++直到把把根节点也执行后就结束

根节点的位置就是i === 1,那当i < 1 时,就无节点可以遍历了,故循环为

for (let i = parseInt(len / 2); i >= 1; i--) {
  sink(arr, i, len)
}

这里的sink函数和我们上面的代码实现是一致的,只不过,函数是独立的,我们需要把我们的数组,下标,及长度传入

这里的长度需要传入,是因为后续操作中我们会对len进行修改,所以不能在函数里直接通过获取arr.length实现

function sink(arr, ind, len) {
  while (2 * ind <= len) {
    let j = 2 * ind
    if (j < len && less(arr, j, j + 1)) j++
    if (!less(arr, ind, j)) break
    swap(arr, ind, j)
    ind = j
  }
}

这里的比较函数是less,表示arr[ind] 小于arr[j]时返回true,所以上面的逻辑是使得更小的元素arr[ind]下沉,即我们实现的是最大堆

除了less还有一个swap辅助函数,这两个函数的实现要具体讲下,因为和上面的堆结构稍微有点不一样

function swap(arr, i, j) {
  i--; j--;
  let temp = arr[i]
  arr[i] = arr[j]
  arr[j] = temp
}
function less(arr, i, j) {
  i--; j--;
  return arr[i] < arr[j]
}

不一样在,在执行操作时,我们对传入的参数都进行了减减操作

何故呢?

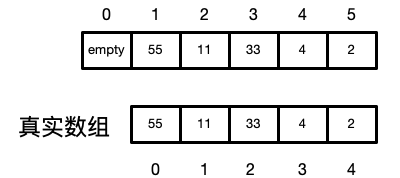
我们在上面的操作时,建立的基础都是把数组的下标从1开始的,所以我们在涉及到真正的数组操作时,下标是从0开始的

就像一个逻辑地址和物理地址的区别,只不过这个转换特别简单的,就是把地址减1

移动

while (len > 1) {
  swap(arr, 1, len--)
  sink(arr, 1, len)
}

现在顶点就是最大值了,现在我们就把首元素和数组的最尾交换

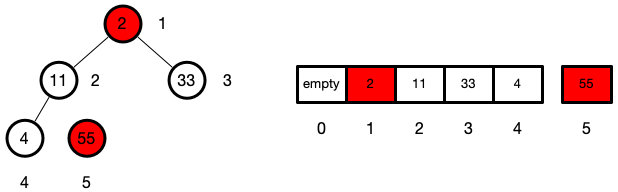
image-20190810220337065

swap(arr, 1, len--)

这里的len--,说明我们首位和尾位交换后,就把堆的长度减减,但是实际上数组是没有改变的,这也是前面使用sink(arr,ind,len)这里要传长度而不是在函数里通过arr.length获取的原因.

此时的数组还是

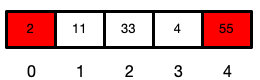
image-20190810220508070

交换后的位置,堆就不是有序的了,所以我们需要把首位下沉

while (len > 1) {
  swap(arr, 1, len--)
  sink(arr, 1, len)
}

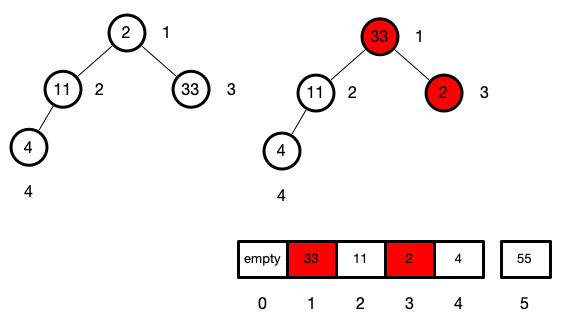
image-20190810221505273

然后我们不断上面的操作

最后我们就会把最大的数都不断累积在后面

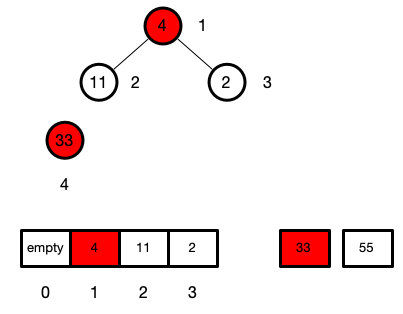
image-20190810221808530

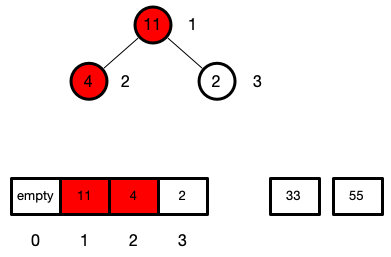
image-20190810222127140

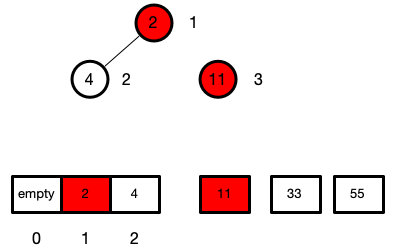
image-20190810222322496

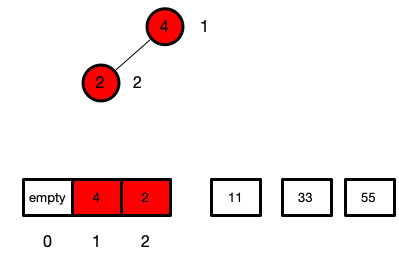
image-20190810222414162

image-20190810222651429

此时堆的长度为1

虽然此时的堆的长度为len === 1

但是这个数组已经就有序了

image-20190810222938948

avatar
文章
阅读
粉丝