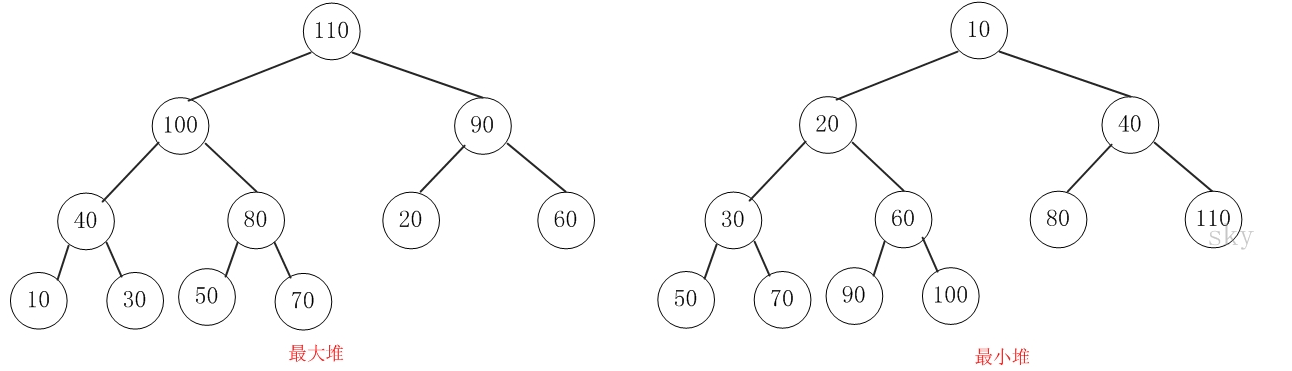
三篇文章我们讲解了优先队列,这节主要讲解二叉堆的实现,通过二叉堆来实现优先队列,废话不多说,我们开始
堆作为优先队列的底层结构,使得入队和出队操作时间复杂度都在O(logn)
什么是二叉堆?
之前我们学习过二叉树,没有了解过二叉堆,从意义字面上还有点相同之处,都有“二叉”两个字(滑稽)
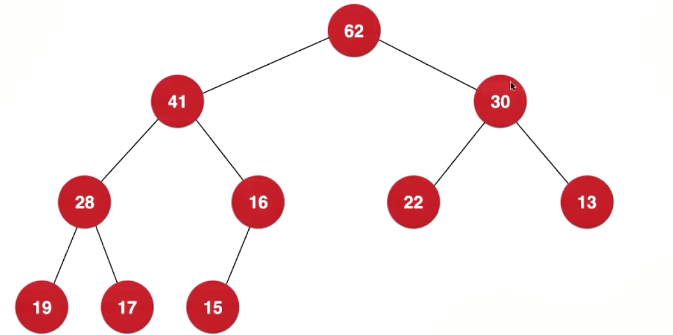
像上图这样的树型结构就是二叉堆,也看不出什么区别啊,就是节点元素值比左孩子小比右孩子大嘛,和二分搜索树一样了。仔细一看还是有点区别的,要想成为二叉堆,必须要满足这样两个条件
- 是一个完全二叉树
- 堆中任意一个节点的值不大于其父亲节点的值
满足上面两个条件就是一个名副其实的二叉堆了,这里我们似乎有扯进了一个新的概念,什么是完全二叉树,搞不懂,蒙圈了,和满二叉树有区别不?有的,满二叉树一定是一个完全二叉树,反过来就不是了,感觉不是很直观,上图一探究竟
满二叉树
上图就是一个满二叉树,也就是说除了叶子节点没有左右孩子,其余节点都有左右孩子,这样的二叉树就是满二叉树
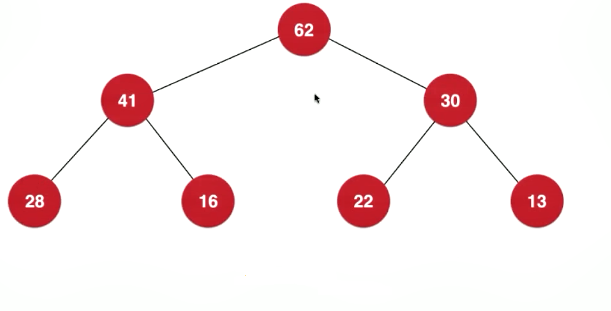
完全二叉树
这个树不一定是满的,可能这个节点没有右孩子,也就是元素一层一层的码放,每一层码放满了后在码放下一层,不满的那一部始终是在这个节点的右侧。
在现实世界中满二叉树的情况还是很少的,更多的情况是像完全二叉树这样,总有那么几个元素孤零零在最后一层,相对来说完全二叉树更适用一些,

我们再来看一下这张图,完全二叉树的叶子节点可能都在最下层,也可能在最下层的上一层,图中就是这样的情况
二叉堆的几个特点
二叉堆有最大堆、最小堆,文章一开始图中就有这俩兄弟,他们唯一的区别在于,父亲节点和孩子节点的关系。最大堆是孩子节点不大于其父亲节点的值,最小堆是孩子节点不小于父亲节点
这里的说的最大是根节点最大,最小是根节点最小,以此类推这个节点都大于他的孩子节点的值或小于。这就是特点一,要么是最大堆,要么是最小堆
在说第二个特点前我们思考一个问题,节点元素的大小与节点所处的层级有关系吗? 从图中看有练习,在上层也就是靠近根节点的元素大于底层元素,结果是这样吗,仔细发现不是这样,从图中可以看到16比19层级要高,但是16的值却比19要小,所以我们得到一个结论就是节点元素的大小与节点所处的层级无关
但是有一点是可以确定的,父亲节点的值要大于孩子节点(这里我们仅仅谈最大堆)
怎么实现二叉堆?
二叉堆用二叉树实现是可以的,但是有没有可以使用其他数据结构来实现呢, 数组可以嘛?
数组作为二叉堆的底层实现
我们说过二叉树中的元素是一层一层的码放的,一层满了再放下一层,而数组的底层设计是开辟一块连续的空间,依次存放数据。有那么一点相同之处,我们大胆的猜测是可以这么做的。
用数组如何表示树的左右孩子呢,有没有规律呢,可以用索引把这种规律给实现了,其实是有规律的,我们给每个节点表上号
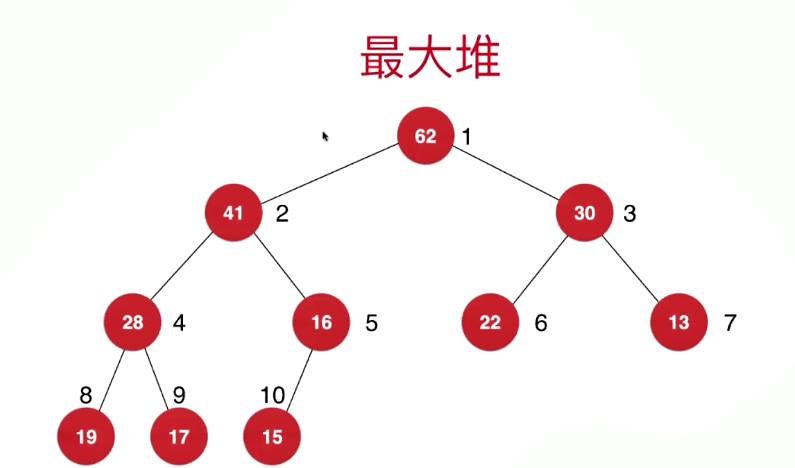
把二叉堆按循序存放在一个数组中

我可以发现这样的一个规律,当前这个节点的左孩子索引为index*2,右孩子为index*2+1,不行我们可以试试,索引为4这节点安装前面的公式得到他的左孩子为8右孩子为9,相应的父亲节点索引的公式为index/2取整
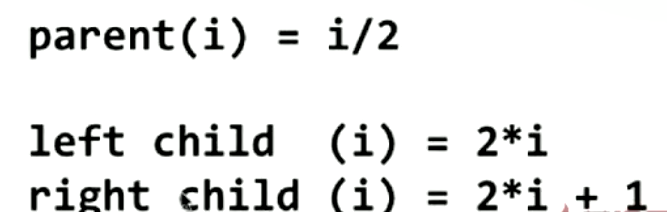
通过这么一个规律我们就用数组来实现二叉树,不过这个数组有点怪,索引为0并没有存放元素,不仅浪费空间而且数组的索引都是从0开始,所以不得不改造一下,让0这个地方存放根节点
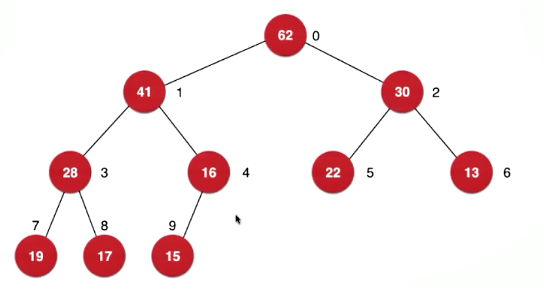
和上面一样把数据存放到一个数组中

就得到一个索引从0开始的数组了,大功告成,等等~,上面的公式还可以用嘛,一一得一,一二得二,掐指一算,糟了,不能用了,前面的推到重来
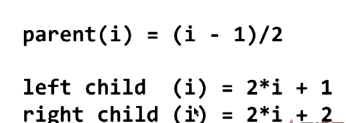
公式来了,这长这样的,有点不一样,毕竟开始索引变为了0
相比用二叉树实现二叉堆,这里我们用数组实现的二叉堆可以根据这个节点找到它的父亲节点,之前我实现的二分搜索树没有这个功能,那是不是说用数组实现二叉堆要好一些呢,这个问题我们后面谈到
用代码堆一个二叉堆的结构出来
贴代码
namespace heap;
/**
* 最大堆
* @package heap
*/
class MaxHeap
{
/**
* 堆元素
* @var array
*/
private $data;
/**
* MaxHeap constructor.
*/
public function __construct()
{
$this->data = [];
}
public function getSize()
{
return count($this->data);
}
public function isEmpty()
{
return count($this->data) == 0;
}
/**返回一个完全二叉树的数组表示中,一个索引表示的元素的父亲节点的索引
* @param $index
* @return int
*/
private function parent($index)
{
if ($index == 0)
throw new \InvalidArgumentException("index-0 does't have parent");
return floor(($index - 1) / 2);
}
/**返回一个完全二叉树的数组表示中,一个索引表示的元素的左孩子的索引
* @param $index
* @return int
*/
private function leftChild($index)
{
return $index * 2 + 1;
}
/**返回一个完全二叉树的数组表示中,一个索引表示的元素的右孩子的索引
* @param $index
* @return int
*/
private function rightChild($index)
{
return $index * 2 + 2;
}
}