相交链表

Category	Difficulty	Likes	Dislikes
algorithms	Easy (46.44%)	364	-

Tags

Companies

编写一个程序，找到两个单链表相交的起始节点。

如下面的两个链表：

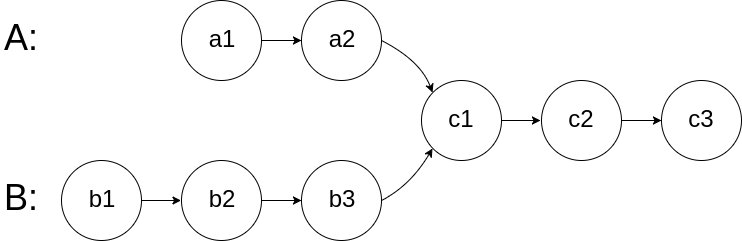
在节点 c1 开始相交。

示例 1：

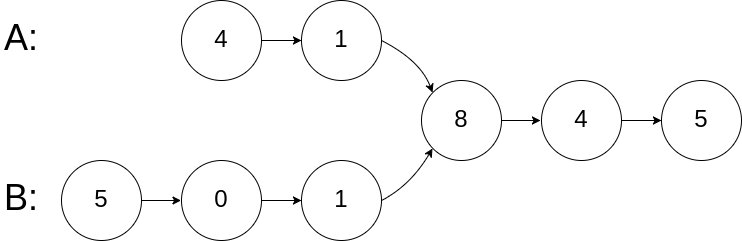
输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3 输出：Reference of the node with value = 8 输入解释：相交节点的值为 8 （注意，如果两个列表相交则不能为 0）。从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,0,1,8,4,5]。在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。

示例 2：

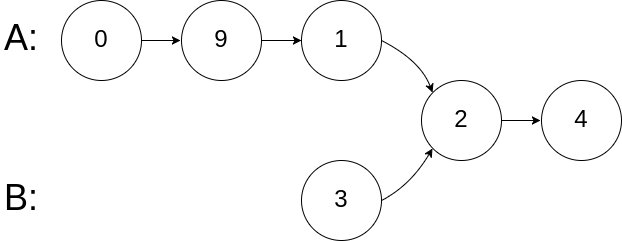
输入：intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1 输出：Reference of the node with value = 2 输入解释：相交节点的值为 2 （注意，如果两个列表相交则不能为 0）。从各自的表头开始算起，链表 A 为 [0,9,1,2,4]，链表 B 为 [3,2,4]。在 A 中，相交节点前有 3 个节点；在 B 中，相交节点前有 1 个节点。

示例 3：

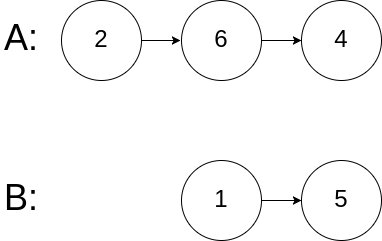
输入：intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2 输出：null 输入解释：从各自的表头开始算起，链表 A 为 [2,6,4]，链表 B 为 [1,5]。由于这两个链表不相交，所以 intersectVal 必须为 0，而 skipA 和 skipB 可以是任意值。 解释：这两个链表不相交，因此返回 null。

注意：

• 如果两个链表没有交点，返回 null.
• 在返回结果后，两个链表仍须保持原有的结构。
• 可假定整个链表结构中没有循环。
• 程序尽量满足 O(n) 时间复杂度，且仅用 O(1) 内存。

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */

/**
 * @param {ListNode} headA
 * @param {ListNode} headB
 * @return {ListNode}
 */
var getIntersectionNode = function(headA, headB) {
    
};

1 set

相交的时候,表示在同一个地方相遇,这个地点是相同的

表明两链表中各存在一个节点指向同一段地址

那么如果我们先后把两条的链表存在在set里面

当我们在添加第二条链时

如果出现添加的节点已经存在

那就说明了两链表相交

var getIntersectionNode = function (headA, headB) {
  const set = new Set()
  while (headA) {
    set.add(headA)
    headA = headA.next
  }
  while (headB) {
    if (set.has(headB)) return headB
    headB = headB.next
  }
  return null
};

注意：我们存储进去的是对象，实际存储的是地址，这样才能判重

set有用会面对一个空间消耗的问题,于是我们思考另一种办法

所以不符合:程序尽量满足 O(n) 时间复杂度，且仅用 O(1) 内存

复杂度分析

• 时间复杂度 :
• 空间复杂度 : 或

2 消差

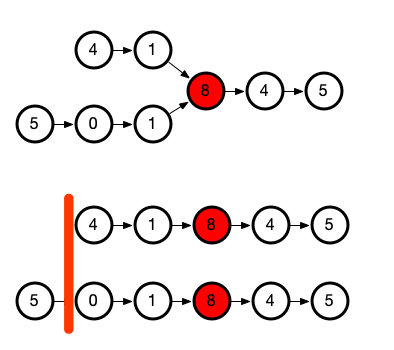
如果两链表的遍历从红色线开始,那每走一步我们就比较两指针的地址

当走到相交指针时,两指针就会相等,那直接返回该指针即可

while (headA && headB) {
  if (headA === headB) return headA
  headA = headA.next
  headB = headB.next
}
return null

那我们现在要做的,就是让两指针从红色线开始,即消除多出来的部分

那就要计算出两链表的长度差,所以我们需要遍历链表获取长度

function getListLength(head) {
  let len = 0
  while (head) {
    len++
    head = head.next
  }
  return len
}

然后使得较长的一条,先走到起跑线,这样长短链表遍历的位置满足上面的条件

let aLen = getListLength(headA)
let bLen = getListLength(headB)
if (aLen > bLen) {
  headA = forwardLongList(aLen, bLen, headA)
} else {
  headB = forwardLongList(bLen, aLen, headB)
}

function forwardLongList(longLen, shortLen, head) {
  let diff = longLen - shortLen
  while (head && diff) {
    head = head.next
    diff--
  }
  return head
}

后续只要调用遍历即可,最终的代码如下

/**
 * @param {ListNode} headA
 * @param {ListNode} headB
 * @return {ListNode}
 */
var getIntersectionNode = function (headA, headB) {
  let aLen = getListLength(headA)
  let bLen = getListLength(headB)
  if (aLen > bLen) {
    headA = forwardLongList(aLen, bLen, headA)
  } else {
    headB = forwardLongList(bLen, aLen, headB)
  }
  while (headA && headB) {
    if (headA === headB) return headA
    headA = headA.next
    headB = headB.next
  }
  return null
};

function getListLength(head) {
  let len = 0
  while (head) {
    len++
    head = head.next
  }
  return len
}
function forwardLongList(longLen, shortLen, head) {
  let diff = longLen - shortLen
  while (head && diff) {
    head = head.next
    diff--
  }
  return head
}

复杂度分析

3 补差

在上面小消差中,我们需要提前遍历以获取长度,然后再重新遍历,代码显得特别冗长

消差既然是为了使得到相交点等距,那等距也可以通过补差获得,比如

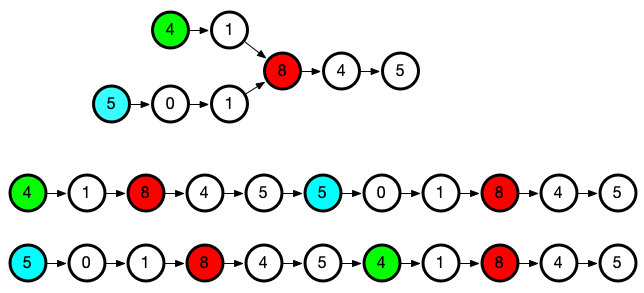
我们在headA后面添加一条headB链表

在headB后面添加一个条headA链表

即

那如图所示,我们就开始同时遍历,每次遍历进行比较,当两指针相同时,即在交点相遇

let curA = headA
while (1) {
  curA = curA === null ? headB : curA.next
}

上面这段代码就表示

1. 先遍历headA,curA = headA
2. 遍历 curA = curA.next
3. 遍历到headA终点了,即curA === null
4. 就开始遍历headB,即curA = headB
5. 遍历 curA = curA.next

那我们让curA和curB同时遍历,则他们会在第二次经历相交点时相遇

等相交时就退出便利直接返回相交点

var getIntersectionNode = function (headA, headB) {
  let [curA, curB] = [headA, headB]
  while (curA !== curB) {
    curA = curA === null ? headB : curA.next
    curB = curB === null ? headA : curB.next
  }
  return curA
}

复杂度分析

时间复杂度 : 空间复杂度 :