反转链表 II

Category	Difficulty	Likes	Dislikes
algorithms	Medium (45.95%)	171	-

Tags

Companies

反转从位置 *m* 到 *n* 的链表。请使用一趟扫描完成反转。

说明: 1 ≤ m ≤ n ≤ 链表长度。

示例:

输入: 1->2->3->4->5->NULL, m = 2, n = 4
输出: 1->4->3->2->5->NULL

/*
 * @lc app=leetcode.cn id=92 lang=javascript
 *
 * [92] 反转链表 II
 */
/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */
/**
 * @param {ListNode} head
 * @param {number} m
 * @param {number} n
 * @return {ListNode}
 */
var reverseBetween = function(head, m, n) {
    
};

1 迭代反转

我们先回顾一下206反转链表

var reverseList = function (head) {
  let [prev, cur] = [null, head]
  while (cur) {
    [cur.next, prev, cur] = [prev, cur, cur.next]
  }
  return prev
};

这道题的区别，只是我们需要反转的链表，是原链表的其中一部分

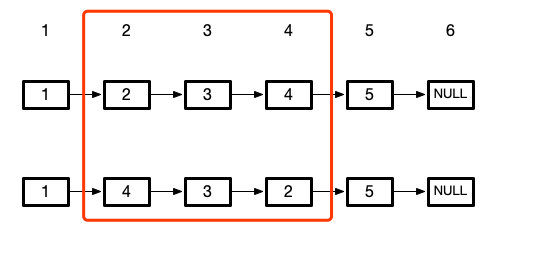
那么需要注意的就有两点

从哪开始

反转链表的"头节点"
到哪结束

反转链表的长度

代码实现

// leetcode 206
var reverseList = function (head) {
  let [prev, cur] = [null, head]
  while (cur) {
    [cur.next, prev, cur] = [prev, cur, cur.next]
  }
  return prev
};

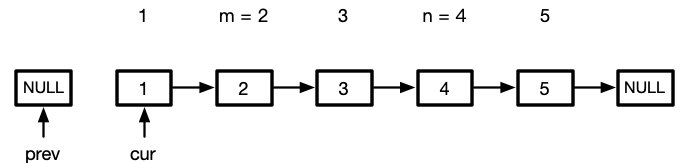
那那我们就在上面206的基础上修改

先让cur达到要反转的时候再开始执行while循环

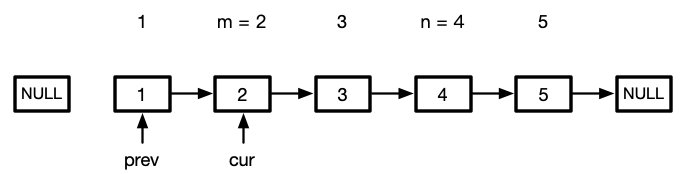
根据上图我们知道m是从1开始算的

let [prev, cur] = [null, head]
while (m > 1) {
  prev = cur
  cur = cur.next
  m--;n--;
}

这里我们可以顺便执行n--,这样当cur到达反转链表的"头节点"时,n刚好等于反转链表的长度

于是我们就可以开始反转链表的了

while (n--) {
  [cur.next, prev, cur] = [prev, cur, cur.next]
}

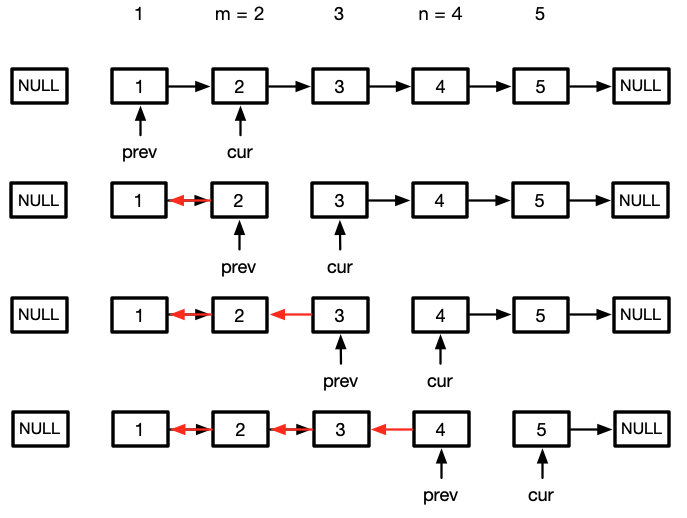
这g 时候我们再来看看我们最后要的效果

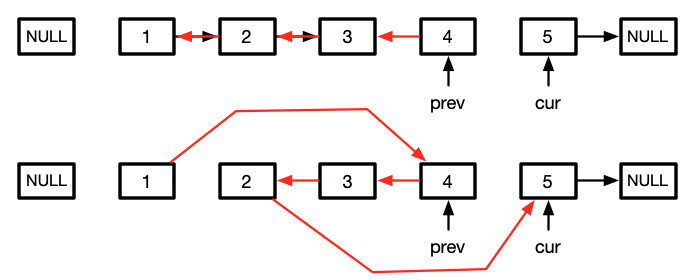
我们还要在修改两个节点的指针

而这两个节点刚好就是cur和prev准备反转链表的位置

故我们可以在反转链表前,缓存这两个节点

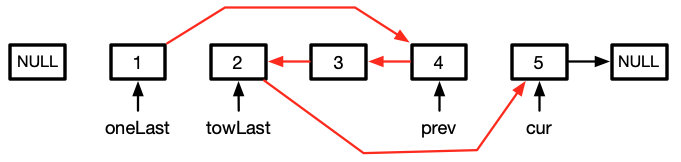
let cur = head
let prev = null
while (m > 1) {
  prev = cur
  cur = cur.next
  m--; n--;
}
let oneLast = prev
let twoLast = cur
while (n--) {
  [cur.next, prev, cur] = [prev, cur, cur.next]
}

然后在反转完链表后我们连接上去

oneLast.next = prev
twoLast.next = cur

最后我们只要返回原始链表的头节点,即head节点就可以了

return head

但是这里我们需要考虑两个问题

m === 1

let cur = head
let prev = null
while (m > 1) {
  prev = cur
  cur = cur.next
  m--; n--;
}
let oneLast = prev

如果m等于 1的话,那么while循环就没有执行,故oneList就是null

我们执行oneLast.next = prev就会报错了,因为oneLast是null所以是没有next属性

而且,我们考虑下面这种情况

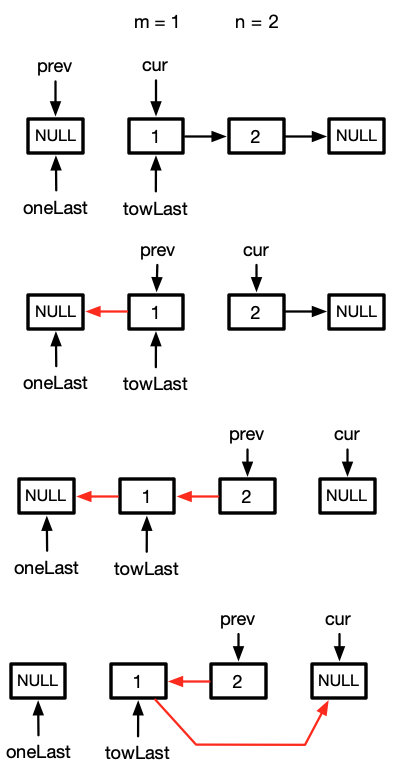
既然oneLast是NULL,即我们是从头开始反转的,所以原本的head就一定不是反转后的头节点了

故我们需要转一个判断,当oneLast为null时,即我们从head就开始反转链表了,那此时的head就一定不是反转后的头节点,我们就要把head设置为反转链表链表的头节点,即prev

还是直接看图比较容易懂,自己看图

oneLast ? oneLast.next = prev : head = prev

故最终代码就是

var reverseBetween = function (head, m, n) {
	let cur = head
	let prev = null
	while (m > 1) {
		prev = cur
		cur = cur.next
		m--; n--;
	}
	let oneLast = prev
	let twoLast = cur
	while (n--) {
		[cur.next, prev, cur] = [prev, cur, cur.next]
	}
	oneLast ? oneLast.next = prev : head = prev
	twoLast.next = cur
	return head
}

复杂度分析

时间复杂度: $O(N)$

1 ≤ m ≤ n ≤ 链表长度,我们从头开始遍历,从m开始交换,直到n结束,n后面的结点是不用遍历更不用交换的
空间复杂度: $O(1)$ 。我们仅仅在原有链表的基础上调整了一些指针，只使用了 $O(1)$ 的额外存储空间来获得结果。

2 递归(栈)

var reverseBetween = function (head, m, n) {
  if (!head) return null
  let [left, right] = [head, head]
  let stop = false
  let recurseAndReverse = (right, m, n) => {
    // 表示right到达需要反转的链表尾端,开始回溯
    if (n === 1) return
    // 每次递归往前之前一步,回溯时就表示往后退一步
    right = right.next
    if (m > 1) left = left.next
    recurseAndReverse(right, m - 1, n - 1)
    // 只有当 n === 1时 才会进入这里
    // 此时 left 和 right 在需要反转链表的首尾

    // left → 相遇  ←right  前者表示奇数时相遇 后者表示偶数时
    if (left === right || right.next === left) stop = true
    if (!stop) {
      // 交换首尾的值
      [left.val, right.val] = [right.val, left.val]
      // left我们一直是引用外部的,所以这个修改是全局的
      // 而right作为栈元素,函数回溯时,就会使用当时的值,就能模拟链表后退
      left = left.next
    }
  }
  recurseAndReverse(right, m, n)
  return head
}

这个写法看起来很难懂,所以会让人觉得好像很厉害,如果我换一种表达,你会觉得这种写法简直就是智障

就是:我们把m~n里数都取出来放入栈中,然后我们再不断的出栈把数依次从从m开始放入,至到n

var reverseBetween = function (head, m, n) {
  let cur = head
  let prev = null
  while (m > 1) {
    prev = cur
    cur = cur.next
    m--; n--;
  }
  let stack = []
  while (n--) {
    stack.push(cur.val)
    cur = cur.next
  }
  cur = prev ? prev.next : head
  while (stack.length) {
    cur.val = stack.pop()
    cur = cur.next
  }
  return head
}

是不是觉得这种方法挺弱智的,就是交换节点的值,而不是改变节点

而上面那个你看不懂的,递归的代码本质就是这么弱智,只不过他的栈是函数栈 ,存储的是节点,而不是存储值

那为什么是存储节点不存储值,是因为智障,因为我们在出栈的时候,可以直接把值放入节点中,智障的存储节点,在放值的时候还需要调用节点.val这样先获取值再存入

那这么智障的写法有什么好处吗?秀呀!秀到别人都看不懂,其实本质就是一个栈

var reverseBetween = function (head, m, n) {
  if (!head) return null
  let [left, right] = [head, head]
  let stop = false
  let recurseAndReverse = (right, m, n) => {
    if (n === 1) return
    right = right.next
    if (m > 1) left = left.next
    recurseAndReverse(right, m - 1, n - 1)
    if (left === right || right.next === left) stop = true
    if (!stop) {
      [left.val, right.val] = [right.val, left.val]
      left = left.next
    }
  }
  recurseAndReverse(right, m, n)
  return head
}

明确left是获取外部函数的,而right是在函数内部的,故每次函数栈里的right是不一样的

算法

我们定义一个递归函数用于反转给定链表的一部分。
将函数记为 recurse。该函数使用三个参数: m 为反转的起点, n 为反转的终点, 以及从第 n 个结点开始，随着递归回溯过程向后移动的指针 right。不清楚的话，可以参考后文的示意图。
此外，我们还有一个指针 left，它从第 m 个结点开始向前移动。在 Python中, 我们需要一个全局变量，值随着递归的进行而改变。在其他函数调用造成的变化可以持续的编程语言中，可以考虑将该指针加为函数recurse\ 的一个变量。
在递归调用中，给定 m，n，和 right, 首先判断 n = 1。若判断为真, 则结束。
于是，当 n 的值达到 1 时，我们便回溯。这时，right 指针在我们要反转的子链表结尾，left 到达了字列表的开头。于是，我们置换数据，并将 left 指针前移：left = left.next。我们需要此变化在回溯过程中保持。
自此，每当我们回溯时，right 指针向后移一位。这就是前文所说的模拟。通过回溯模拟向后移动。
当 right == left 或者 right.next == left 时停止交换。当子链表的长度为奇数时，情况为前者；当子链表长度为偶数时为后者。我们使用一个全局 boolean 变量 flag 来停止交换。

下面是一系列整个算法的示意图，希望能够帮助你理解清楚。

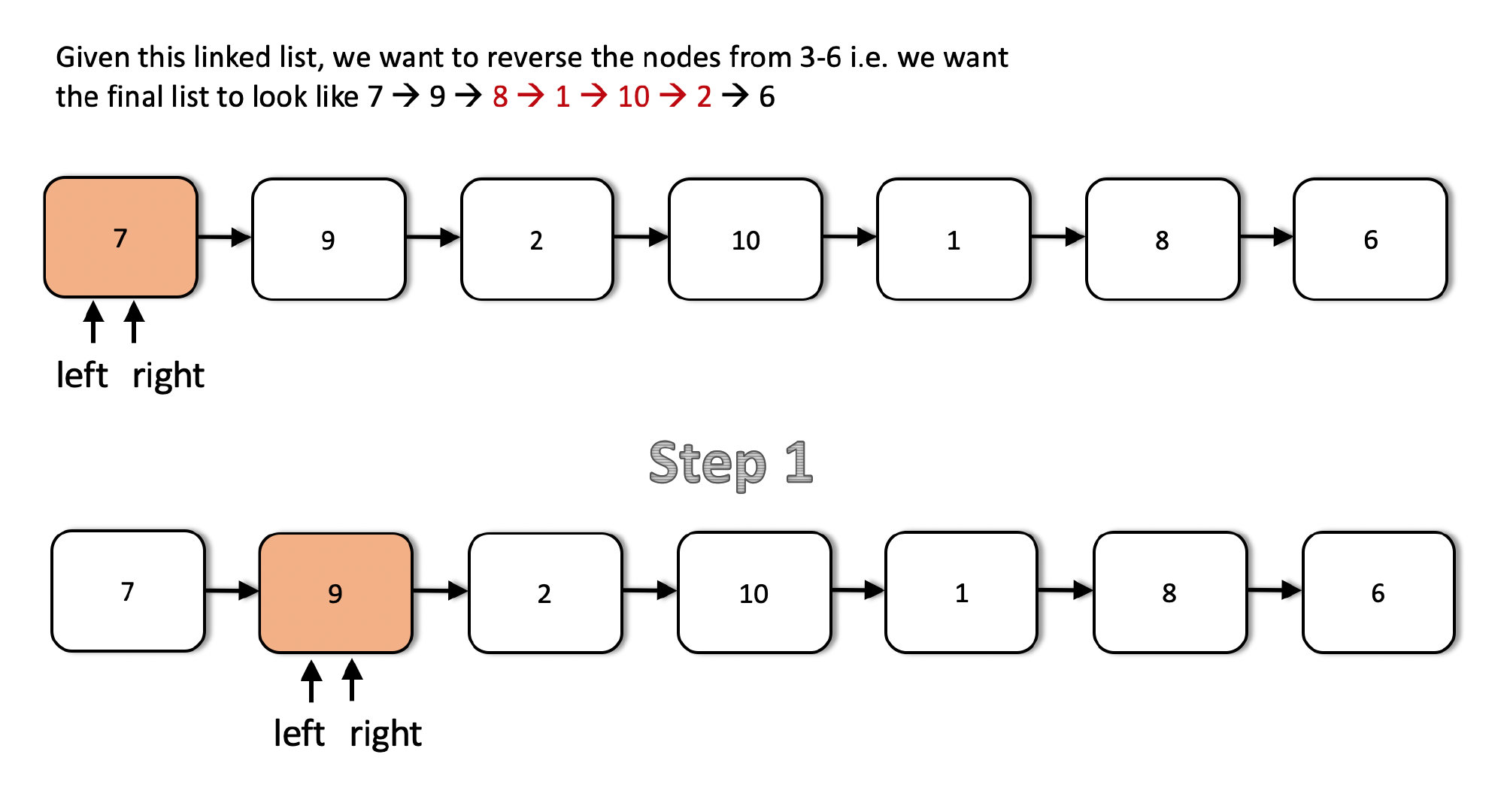
这是递归过程的第一步。给定所用链表，left 和 right 指针从链表的 head 开始。第一步是以更新过的 m 和 n 进行递归调用，换而言之，它们的值各自减 1。此外，left 和 right 指针向前移动一位。

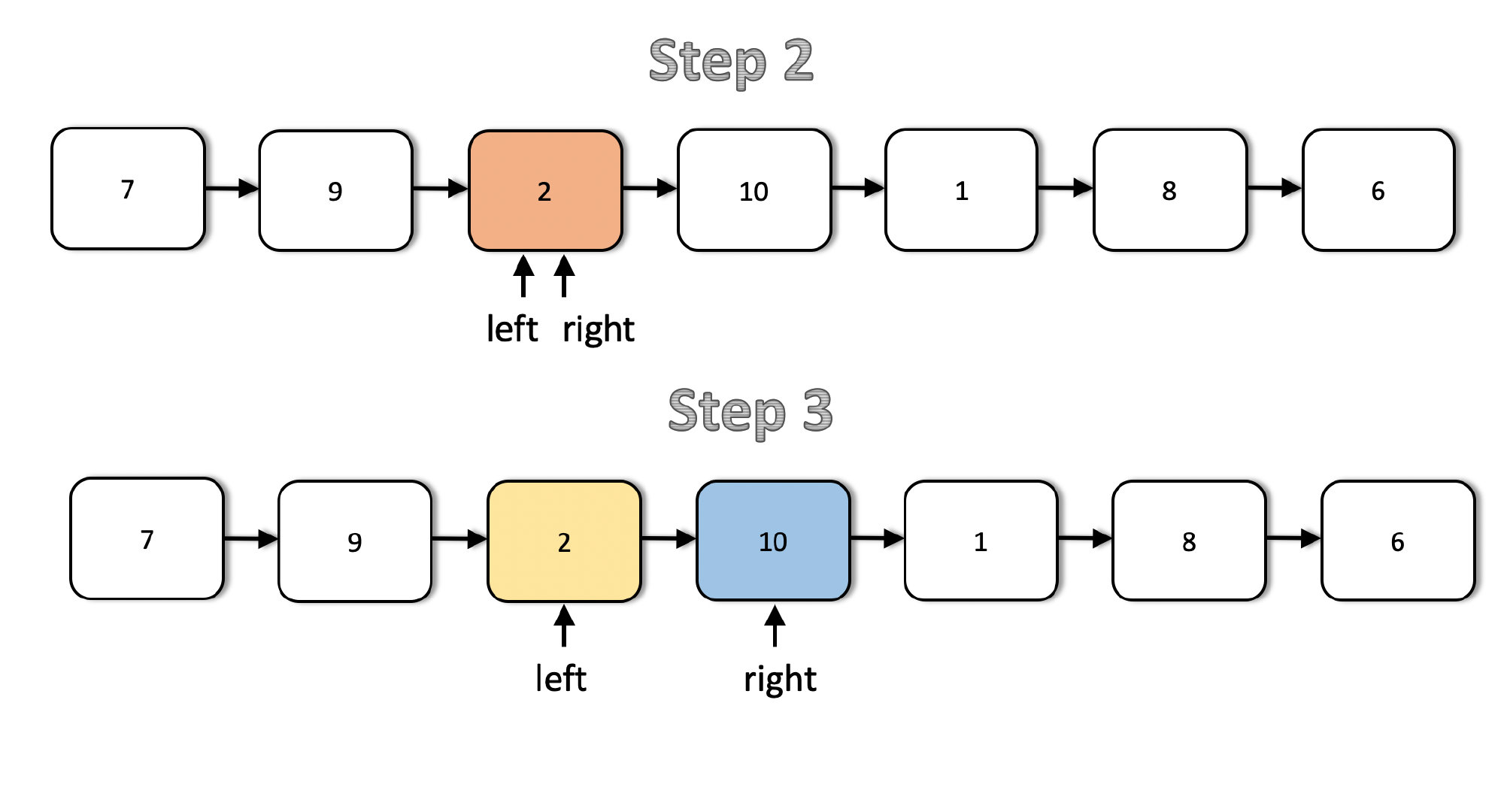
接下来的两步展示了 left 和 right 指针在链表中的移动。注意到在第二步之后，left 指针抵达了目标位置。因此，后续不再移动。从现在起，只有 right 指针继续移动，直到抵达结点 6。

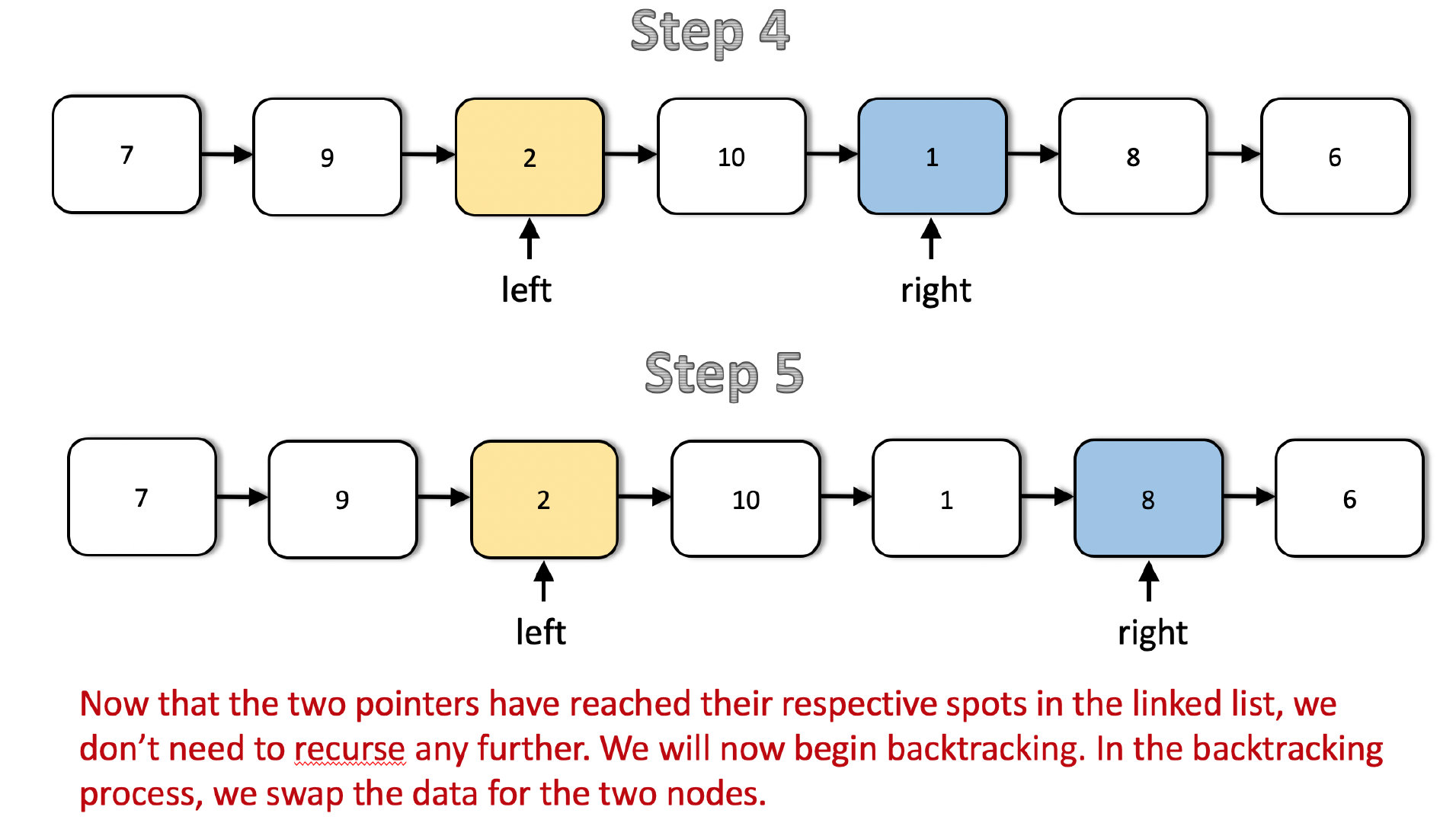
如你所见，在第五步之后，两个指针均抵达了目标位置，可以开始进行回溯。我们不再继续递归。回溯过程中的操作是交换 left 和 right 结点的数据。

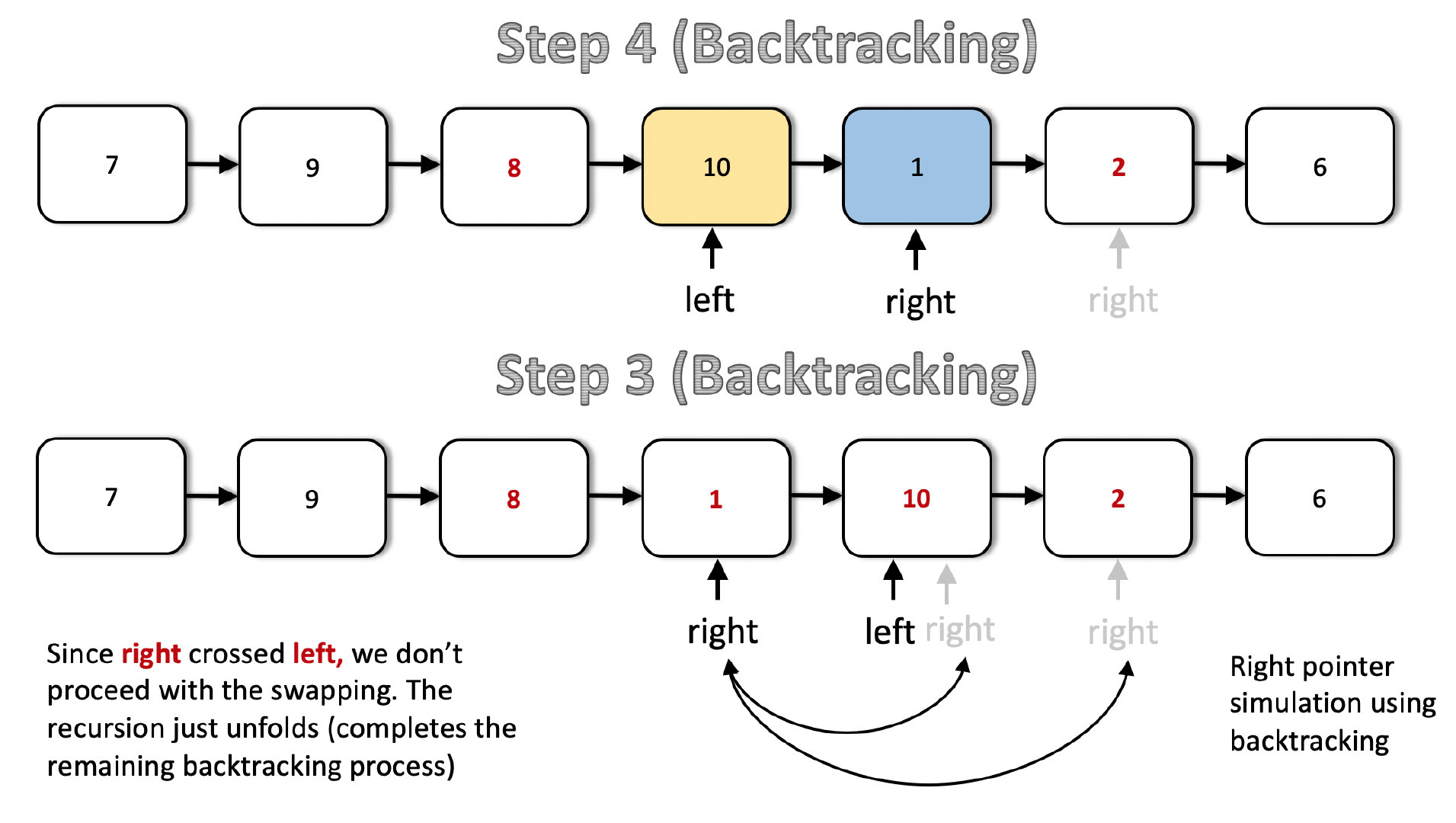
如你所见，在第三步（回溯）之后，right 指针 穿过了 left 指针，此时已经完成了要求部分链表的反转。结果是 [7 → 9 → 8 → 1 → 10 → 2 → 6]。于是不再进行数据交换，在代码中，我们使用全局 boolean 变量 flag 来停止数据交换。不能直接跳出递归。

复杂度分析

时间复杂度: O(N)

对每个结点最多处理两次。一次是递归过程,一次是在回溯过程.在回溯的过程中,我们只回溯了一半的节点就完成全部交换，但总复杂度还是 O(N)。
空间复杂度: 最坏情况下为 O(N)。

在最坏的情况下，我们需要反转整个链表。这是此时递归栈的大小。

092反转链表II(JS)

反转链表 II

1 迭代反转

代码实现

复杂度分析

2 递归(栈)