Numpy 中的 axis 对初学者而言是一个非常容易引起困扰的概念,本文希望通过图文并茂的方式,让大家能对 axis 有一个直观的认识。
数形结合百般好
数缺形时少直观,形少数时难入微。
数形结合百般好,隔离分家万事休。
—— 华罗庚
axis 本身就是 轴 的意思,它实际上代表了要在哪个轴上进行求和,所以使用 sum 函数时,一定要有一个空间上的概念,这样会非常容易理解计算的结果。
二维
所以当我们说 [[0, 4, 2], [-2, 5, 3]],我们说的其实是:
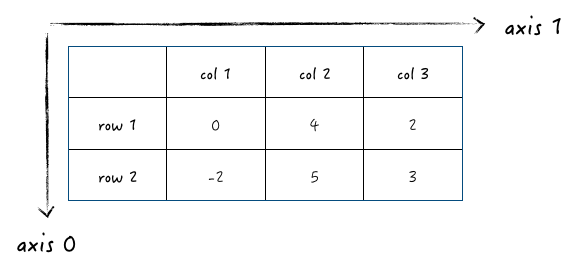
二维数组对应的就是一个二维表格,它一共有两个轴(axis),axis 0 对应行,axis 1 对应列。
当指定 axis 0 进行求和时,做的是这样的运算:
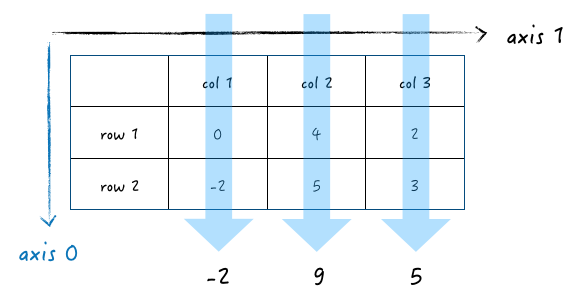
也就是顺着 axis 0 轴求和,最后得到一个一维数组:
>>> np.sum([[0, 4, 2], [-2, 5, 3]], axis=0)
array([-2, 9, 5])
同样地,当指定 axis 1 时,是这样的:
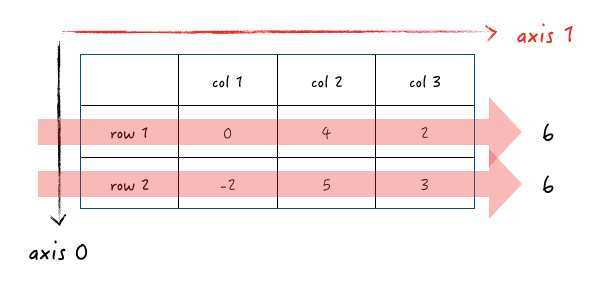
即:
>>> np.sum([[0, 4, 2], [-2, 5, 3]], axis=1)
array([6, 6])
三维
上升到三维空间又是怎样的呢?实际上道理还是一样的,我们创建一个三维数组:
>>> array_3d = [
... [
... [1, 2],
... [3, 4]
... ],
... [
... [5, 6],
... [7, 8]
... ],
... [
... [9, 10],
... [11, 12]
... ]
... ]
然后脑海里马上就有一个三维的空间了!
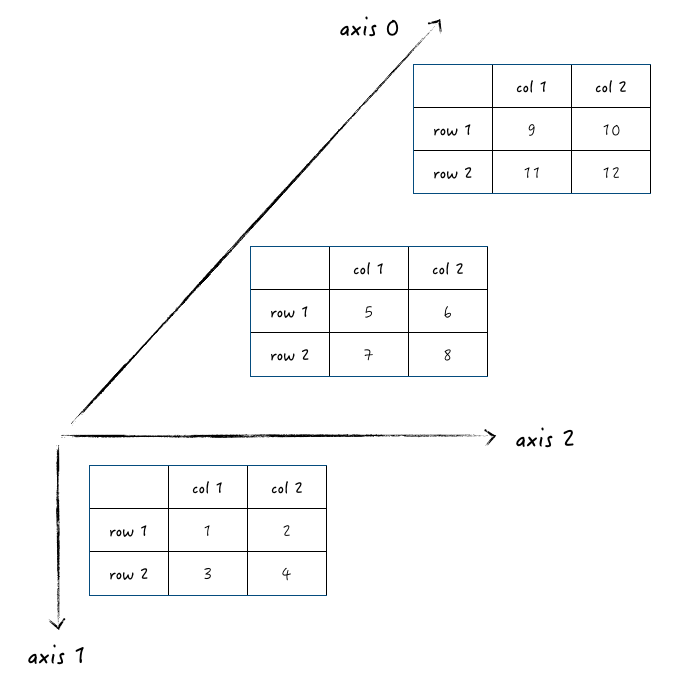
那对 axis 0 求和,其实就是顺着 axis 0 的方向求和,最后得出的是一个二维数组:
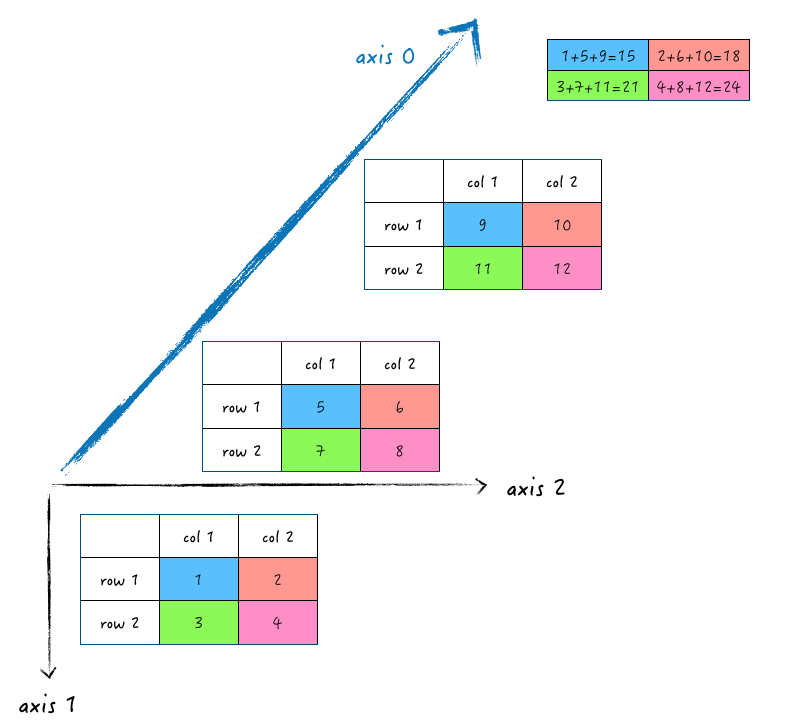
即:
>>> np.sum(array_3d, axis=0)
array([[15, 18],
[21, 24]])
对 axis 1、axis 2 也是一样的,这里以 axis 2 举例,大家可以尝试自己画 axis 1 的:
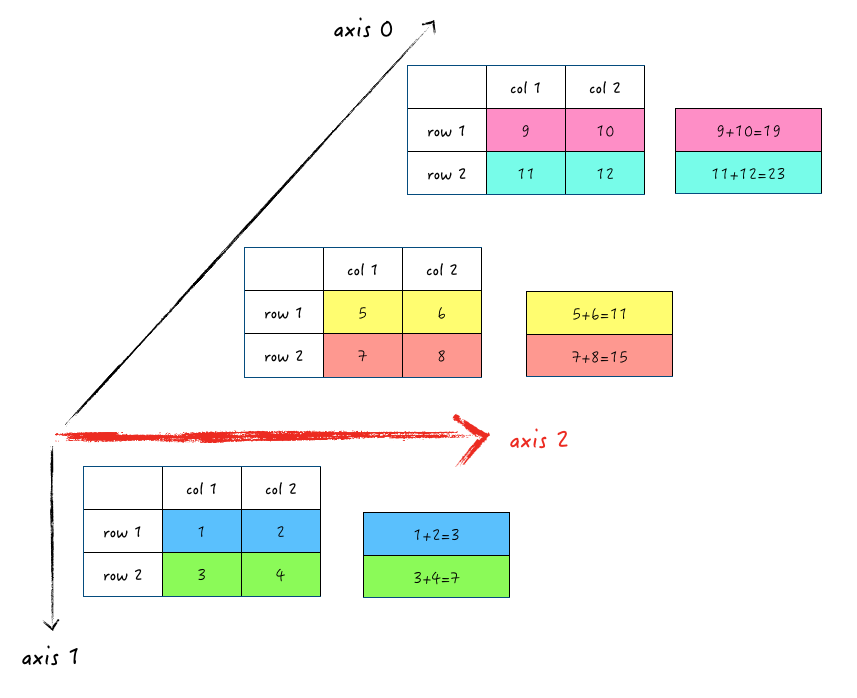
>>> np.sum(array_3d, axis=2)
array([[ 3, 7],
[11, 15],
[19, 23]])
四维咋办
四维咋办,四维还真不好画,不过本文的目的是能够直观理解计算的结果,讲道理前面这些图应该足够理解求和了,所以我也不画了,哈哈哈
轴的确定
当然,上面所有运算的前提,都是我们正确确定好了坐标轴的方向。关键问题在于,如何知道哪个是 axis 0、哪个是 axis 1?
实际上,轴的确定可以根据嵌套关系来确定,轴的顺序就是括号的从外到内:
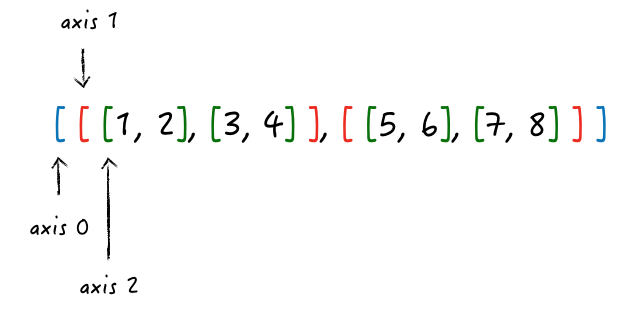
不过用这种方式思考,就少了对形的理解,会稍微难以理解,可以参考 Python · numpy · axis。